Научная электронная библиотека

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

6.3.3. Влияние сужения берегов на параметры ИГВ

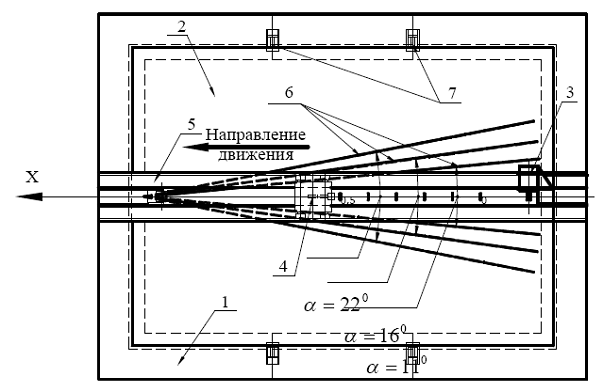
В реальных условиях эксплуатации при посадке самолета в заливах, проливах, а также в узких местах акватории рек, когда имеет место сужение берегов, актуальной остается проблема учета влияния таких ледовых условий на несущую способность ледяного покрова. С целью исследования данной проблемы в опытовом бассейне была проведена серия экспериментов, в процессе которых были получены кривые профиля ИГВ, возникающих при движении модели нагрузки по неразрушаемому сплошному льду. На рис.6. 21. приведена схема экспериментальной установки для исследования влияния сужения берегов на параметры ИГВ.

Рис.6.21. Схема экспериментальной установки для исследования влияния сужения берегов на параметры ИГВ (1 – планширь чаши бассейна; 2 – модельный слой; 3 – электродвигатель буксировочной системы; 4 – тележка для перемещения нагрузки; 5 – направляющие для тележки; 6 - вертикальные пластины; 7 – кронштейны для крепления подвесного дна).

Движение нагрузки происходило из широкой части в узкую (это наиболее опасный для сохранения несущей способности ледяного покрова режим). Анализ полученных данных проводился с помощью зависимости (6.10). Соотношения параметров ИГВ, характеризующих влияние угла сужения берегов акватории на напряженно-деформированное состояние ледяного покрова производилось через параметр , т.е для сохранения несущей способности ледяного покрова при рассматренной ледовой обстановке было принято условие:

(6.13)

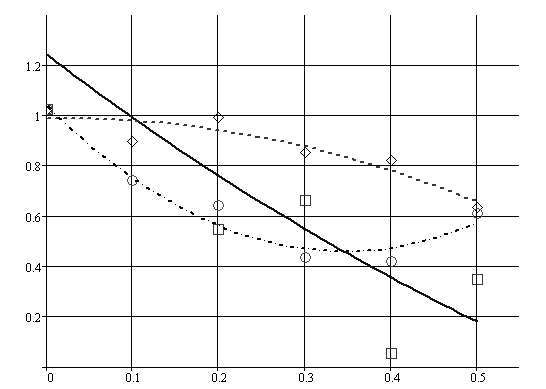
Зависимость отношения от координаты X представлена на рис.6.22, где X - обозначено расстояние, проходимое нагрузкой от точки старта.

Рис.6. 22. Экспериментальные зависимости от координаты X

( - , - , - ).

Из графика следует, что при углах между вертикальными пластинами 4 и параметр уменьшается по мере увеличения X. При этом для угла уменьшение происходит медленнее, чем при . При - имеет минимум при X » 0,35 м.

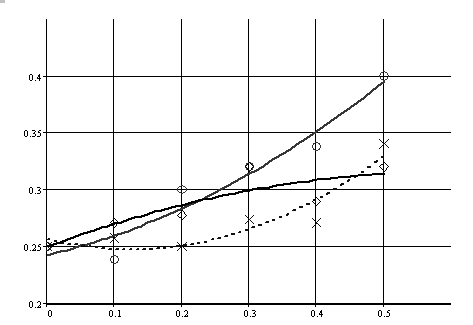
Слабо выраженную корреляцию между и X, а также существенный разброс данных, представленных на рис.6.22, можно объяснить влиянием, оказываемым отраженными от стенок ИГВ на волнообразование вблизи линии движения нагрузки. Вследствие этой интерференции происходит трансформация параметров возбуждаемых ИГВ, приводящая к уменьшению их амплитуд A и к увеличению длин . Это видно на рис.6.23, 6.24, где представлены экспериментальные зависимости амплитуды A и длинны ИГВ от координаты X.

Как видно из графиков, амплитуда ИГВ увеличивается в направлении оси X только при значении угла . При значениях угла и амплитуда ИГВ меняется незначительно с также незначительно выраженным минимумом при x» 0,15…0,30 м. Вместе с амплитудой для угла наблюдается рост и длины ИГВ , на всем пути движения нагрузки вдоль оси X. Из этого следует, что для решения данной задачи требуются дополнительные исследования.