Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

6.3.8. Основные результаты экспериментов с использованием модели неразрушаемого ледяного покрова

Используя полученные экспериментальные данные, можно учитывать влияния исследованных ледовых условий на интенсивность ИГВ, возникающих в процессе воздействия нагрузки (самолета) на ледяной покров, а следовательно, прогнозировать его несущую способность. Для этого достаточно выполнить пересчет смоделированных параметров на натуру: глубину H, расстояние между параллельными берегами B, координату положения самолета на оси Xпри его движении в условиях сужения берегов или наклона дна вблизи берега. Для этого можно использовать графики, приведенные на рис. 6.15, 6.20, 6.22, 6.26, 6.30, 6.33 - 6.36.

1. Глубина водоема.

В качестве безразмерной глубины была использована величина kH,.гдеkможно определить по одной из следующих зависимостей:

- глубокая вода;

- мелкая вода.

В результате получена зависимость, позволяющая учесть влияния глубины водоема на интенсивность возникающих ИГВ (см. рис. 6.37).

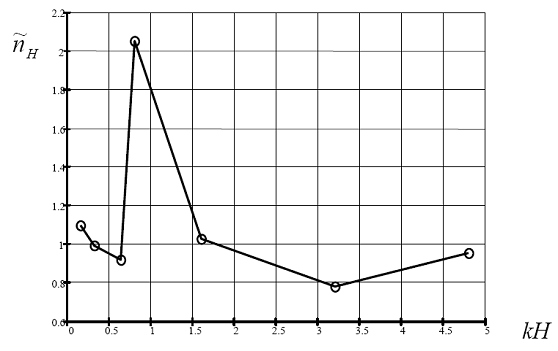
Рис. 6.37. Зависимость коэффициента влияния глубины от величины kH.

2. Расстояние между параллельными берегами.

В условиях интерференции ИГВ, когда происходит наложение возбуждаемых и отраженных волн, в качестве безразмерного расстояния между параллельными берегами можно принять величину , определяемую как отношение ширины акватории Bк длине резонансных ИГВ :

.

Значения длин резонансных ИГВ были определены экспериментально и подтверждены с помощью теоретических зависимостей динамики ледяного покрова [124] (см. табл. 6.1):

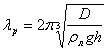- глубокая вода;

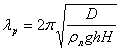- мелкая вода.

В результате была построена безразмерная зависимость, позволяющая учитывать влияние близости берегов на интенсивность возникающих ИГВ (см.рис.6.38). На рисунке отмечены кривые, соответствующие максимальным (max) и минимальным (min) значениям .

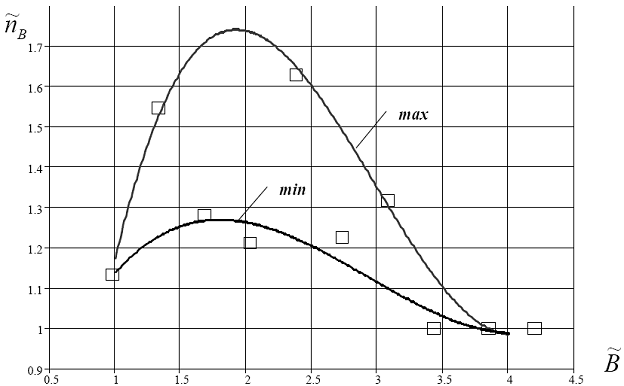
Рис.6.38. Зависимость коэффициента влияния близости берегов от относительногорасстояния между параллельными берегами .

3. Координата Xположения самолета при движении в условиях сужающихся берегов, наклонности дна, а также их комбинации.

В зависимости от близости расположения параллельных берегов возникала различная интерференция возбуждаемых и отраженных ИГВ. Поэтому в качестве безразмерной координаты, определяющей положение нагрузки (самолета) на оси X при учете сужающихся берегов, наклонности дна и комбинации этих факторов, было принято отношение:

,

где X- координата положения нагрузки в направлении движения в модельных экспериментов. В результате были построены зависимости, позволяющие учесть влияния рассматриваемых факторов на интенсивность возбуждаемых ИГВ (см. рис. 6.39 - 6.43).

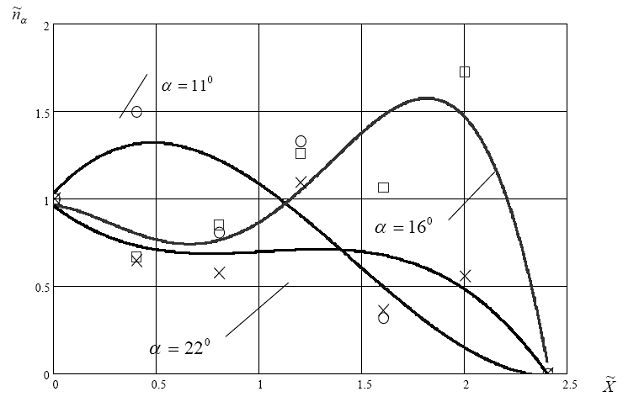
Рис. 6.39. Зависимость коэффициента учета сужения береговот относительной координаты для различных углов сужения .

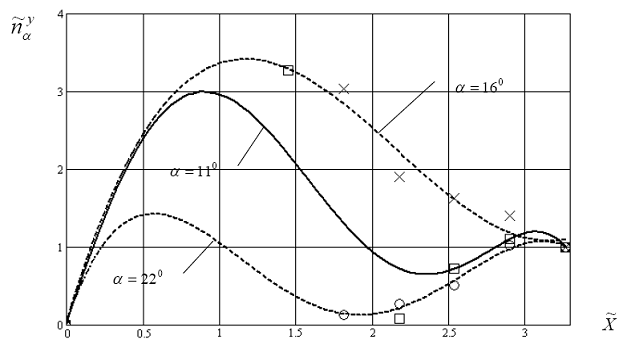
Рис. 6.40. Зависимость коэффициента от относительной координаты ,в случае посадки самолета с ударом.

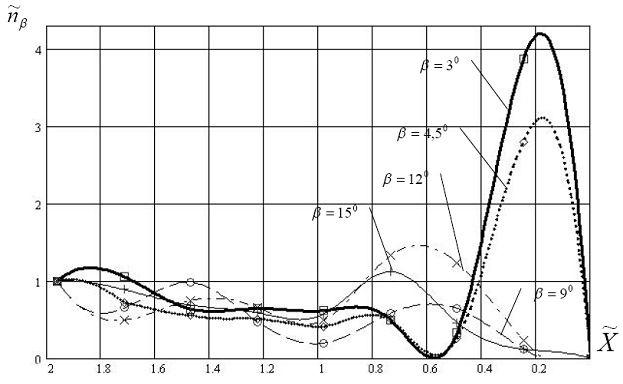
Рис. 6.41. Безразмерная зависимость коэффициентаот расстояния до берега .

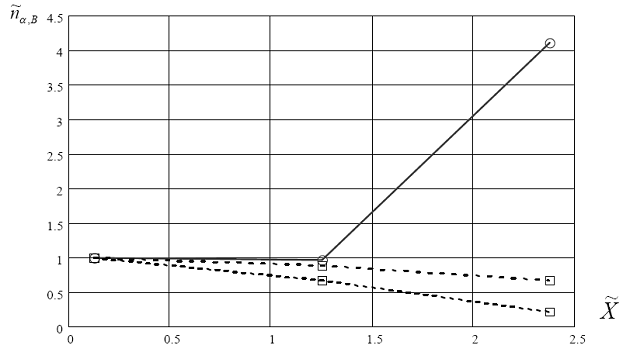
Рис.6.42. Зависимость коэффициента , учитывающего влияние близости берегов совместно с наклоном дна при выходе нагрузки (самолета) на берег от относительной координаты .

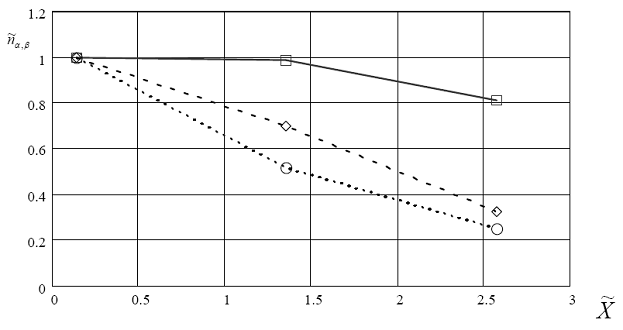
Рис.6 43. Зависимость коэффициента , учитывающего влияние сужение берегов совместно с наклоном дна при выходе нагрузки (самолета) на берег от относительной координаты .