
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

ПОЛИАСПЕКТНАЯ ПОДГОТОВКА СОВРЕМЕННОГО ПЕДАГОГА
Ахметжанова Г. В., Руденко И. В., Груздова И. В., Дрыгина Е. Н., Кустов Ю. А., Медник Г. А., Сундеева Л. А.,
Глава II. СИСТЕМНО-ДЕЯТЕЛЬНОСТНЫЙ ПОДХОД К РАЗВИТИЮ ПЕДАГОГИЧЕСКОЙ ФУНКЦИИ ЛИЧНОСТИю.© Ахметжанова Г.В.
Принцип системности, который был подготовлен развитием естествознания, философии и других наук, может быть положен в основу разработки различных сложных интегрированных образовательных систем.
Приступая к проектированию образовательных систем, необходимо изучить законы их формирования и функционирования. Окружающий нас мир и мы сами как по отдельности, так и все вместе - системы. Любое изменение одной из систем ведёт к изменению в большей или меньшей степени соприкасающихся с ней систем. Таким образом, элемент какой-то данной системы из-за иерархической структуры мира сам оказывается системой со своими элементами. Рассматриваемая же система оказывается элементом другой, вышестоящей по иерархии системы.
Система определяется структурой и её поведением (функционированием). Под структурой понимается постоянная во времени фиксированная связь между элементами системы, изображаемая графом, под поведением - её действие во времени.
Функционирование (поведение) социальных и образовательных систем, а также решающих подсистем может быть основано на следующих принципах: вещественно-энергетического баланса, гомеостаза, выбора решений, перспективной активности или потребного будущего, рефлексии, понимания, осознания и прогнозирования будущего [8].
Рефлексивные системы - это системы, обладающие интеллектом, они тоже включают в себя все перечисленные принципы поведения. К таким системам следует отнести образовательные системы.
Любой закон и любая наука в целом - это модели действующих систем, позволяющие предсказывать поведение реальных объектов в определенном диапазоне условий. Описание системы - это модель, отображающая определенную группу свойств системы, углубление описания - детализация модели. Каждая система требует своего описания, поэтому под описанием систем мы будем понимать модели систем [1].
Как известно, любое научное обоснование связано с установлением зависимости воздействие - результат. Воздействие подается на вход системы, результат фиксируется на выходе. Некоторые науки занимаются разработкой моделей, которые выражают строгую однозначную зависимость между состоянием входа Х и состоянием выхода Y, заданную при помощи переходной функции Y = R(Х), где R - оператор преобразования (R-преобразование). На ранних этапах развития науки ш-преобразование понималось только как однозначная детерминированная функция и только позднее, под давлением фактов, получила вероятностное толкование. ш-преобразование получает вероятностный смысл, так как оно составлено на основании стохастической модели процесса. Функциональные (феноменологические) свойства модели характеризуются ш-преобразованием, поэтому мы будем называть R-преобразование функциональным описанием системы.
Назовем случайным событие, возникающее в результате взаимодействия нескольких независимых событий, каждое из которых либо детерминировано, либо случайно в таком же смысле.
Взаимодействующие объекты образуют систему, входные характеристики которой можно представить как ее описание до взаимодействия, а выходные - после взаимодействия.
Случайность исхода определяется тем, что взаимодействие может происходить в любой момент времени и в диапазоне (множество моментов) времени при разнообразных состояниях объектов. Если механизм взаимодействия (состояния, время, соответствующие состояниям исходы) точно известен, то ш-преобразование есть детерминированная функция X. Если механизм неизвестен, то при многократно повторяющихся однотипных взаимодействиях проявляются ведущие тенденции (в виде повторяющихся ситуаций) и возникает распределение частости исходов. Тогда R-преобразование представляется распределением вероятности в ансамбле случайных событий, такой ансамбль (если он существует физически) рассматривается как стохастическая система.
Модель отнюдь не субъективна, хотя ситуация в ней оценивается с позиций наблюдателя (такая позиция неизбежна, так как R-преобразование отражает уровень знаний наблюдателя, его модель действительности). R-преобразование может задаваться алгебраическим, логическим, дифференциальным оператором; скалярным, векторным или матричным, составленным на основании измерения внешних характеристик или на основании знания устройства системы - морфологического описания.
Предположение об однозначности R-преобразования лежит в основе естественнонаучной концепции и целенаправленной деятельности, которая всегда опирается на явный или скрытый детерминизм. Точные науки занимаются исследованием и таких моделей, которые не содержат R-преобразования. Эти модели хаотические, слабо структурированные, неустойчивые; они обычно недолговечны, в них сталкивается множество независимых событий, не имеющих устойчивых распределений вероятностей. Они характеризуются изменяющимися параметрами, отображающими такой уровень изменения систем, при котором невозможно составление устойчивых морфологического и функционального описаний.
Описание уровня организации отражает как сущность организации, так и наше знание о ней, поэтому такое описание целесообразно назвать информационным. Информационное описание дополняет функциональное и морфологическое. Морфологические свойства систем связываются с функциональными тенденциями только качественно, качественными являются и функциональные описания.
Основное свойство образовательных систем состоит в их целенаправленности, которое понимается, как способность к выбору поведения в зависимости от выбранной цели. Внешние характеристики (выходы) образовательных систем определяются не только внешним воздействием (входами), но и целью. Система каждый раз заново формирует свое R-преобразование, исходя из цели, поэтому однозначного R-преобразования не существует. Поведение целенаправленной системы g зависит от входного воздействия Х и от предполагаемого его изменения Х1(t, g ), которое зависит и от поведения Z. Поэтому с учетом цели Z Y = R(Z; X, X1(g, t)), но X1(g, t) = X1(Y1), где Y1 - самооценка выходных характеристик, которая, в свою очередь, строится на основании X1, X2(Y2) (X2, Y2 - оценки второго порядка, построенные в предположении, что Y = Y1).
Таким образом, в принципе Y = R(Z; X1[Y1(X1, X2{Y2[X2, X3(.) ...YN(.)]}]).
Практически эта итеративная схема, включающая в качестве компонентов экстраполяцию входа и выхода, обрывается довольно быстро из-за ограниченных возможностей системы. Значит, на первый план научного исследования выдвигаются, во-первых, тенденция поведения, во-вторых, цель [7].
Системы, способные формировать R-преобразование применительно к своей внутренней цели, исходя из конкретного состояния входа, - это сложные системы, способные управлять своим поведением. Они могут по-разному реагировать на одинаковые внешние воздействия и одинаково реагировать на различные воздействия. Любые системы можно рассматривать как частный случай сложных систем, поэтому описание образовательной системы, на наш взгляд, следует начинать с трех точек зрения:
1) функциональной;
2) морфологической;
3) информационной.
Функциональное описание исходит из того, что всякая система выполняет некоторые функции - существует, служит областью обитания другой системы, является контрольной для некоторого класса систем, служит средством или исходным материалом для создания более совершенной системы и т.д. Система может быть однофункциональной или многофункциональной. Функциональное описание иерархично. Функция системы представляется числовым функционалом, зависящим от функций, описывающих внутренние процессы, либо качественным функционалом. Функциональное описание должно отражать следующие характеристики сложных и слабо познанных систем: параметры, процессы и иерархию.
Морфологическое описание дает представление о строении системы, оно тоже иерархично. Конкретизация морфологии дается на стольких уровнях, сколько их требуется для создания представления об основных свойствах системы. Морфологические свойства системы существенно зависят от характера связи, а морфологическое описание может включать указание на наличие и виды связей, содержать общую характеристику связей либо их качественные и количественные данные.
Информационное описание дает представление об организации системы. Организованность, упорядоченность системы - способность предопределить свою перспективу, свое будущее.
Согласно основным положениям общей теории систем, человечество есть социальная система, параметрами функциональной цели которой являются: природно-производственная база, интеллект, здоровье, организованность [5] и уровень развития педагогической функции.
Система «человек» двойственна и едина, что находит свое отражение в законе единства и борьбы противоположностей. С одной стороны, человек есть биологическая система, целью которой является сохранение себя как части природной системы, с другой - личность - социальная система, цель которой сохранение себя как элемента социальной системы.
Биологическая система реализует свою функциональную цель по отношению к природе и виду, а личность реализует функциональную цель по отношению к обществу. Друг без друга эти системы существовать не могут [6].
Значимость личности для человечества определяется качеством выполнения ее функций по отношению к природе и обществу, и самая главная из них - педагогическая.
Исходя из вышесказанного, мы рассматриваем личность на основе системного подхода, как систему, являющуюся частью вышестоящих систем «общество» и «природа». Рассмотрение личности как системы характерно для работ Д.М. Мехонцевой. Целью и смыслом существования человека является полноценная жизнь, включающая в себя гармоничное взаимодействие с окружающей средой и обществом. Гармония достигается только тогда, когда все от этого взаимодействия получают пользу. Для этого нужно сформировать у человека полезные потребности и удовлетворить их. Первое необходимо, прежде всего, для Природы, второе - для человека, составляющего общество, следовательно, и для общества в целом.
Другая объективная целостность систем состоит в том, что система имеет функцию - «обязанность» по осуществлению цели вышестоящей системы, а это есть функциональная цель системы.
Наличие этих двух целей - главной и функциональной - объясняется тем, что любая система существует как целое и как часть. Как целое, она имеет своей целью самосохранение, а как часть вышестоящей системы, она выполняет определенные функции по отношению к ней.
Таким образом, в любой системе существуют две объективные цели: собственная (главная) - самосохранение и функциональная (функция) - сохранение вышестоящей системы, в которую она входит как часть. Эти цели являются системообразующими факторами, причиной существования системы [5] .
Параметры главной цели выделены в соответствии с иерархией потребностей, предложенной А. Маслоу, что, в нашем понимании, логично соотносится с главной целью человеческой деятельности - удовлетворение собственных потребностей.
Обозначим уже указанные параметры главной цели:
А1 - Физиологические потребности, обеспечивающие выживание;
А2 - Потребность в безопасности физической и психологической (и уверенности в будущем);
А3 - Потребности социального взаимодействия (в привязанности, поддержке, создании коммуникативных связей);
А4 - Потребности в уважении и признании;
А5 - Потребности в самовыражении и самореализации.
Достижение функциональной цели системы по определенному параметру зависит не только от качества выполнения ею своей функции по этому параметру, но и от реализации ею своей главной цели. Для исследования введем математические символы: (Г - главная цель системы; Ф - функциональная цель системы, L - оператор; Ф - функционал; А, В - параметры главных целей систем; i - номер системы; j - ранг системы; Фij(Аi) - функциональная цель i-й системы j-го ранга по параметру Аi; m - номер параметра, f - функция, выполняемая системой; opt - оптимум; a - весовой коэффициент).
Д.М. Мехонцева определила операторный вид зависимости главной цели Г от совокупности функциональных целей Ф в виде уравнения
![]() ;(1)
;(1)
![]() ,(2)
,(2)
![]() (3).
(3).
Из (1) и (2) вытекает (3) - закон сохранения систем. Этот основополагающий вывод Д.М. Мехонцевой трактуется следующим образом: достижение главной цели - самосохранение любых систем зависит от качественного выполнения всеми ее подсистемами своих функций, т.е. реализацию функциональной цели, направленной на сохранение вышестоящей системы и главной цели - их самосохранения [6, с. 173].
В символической формуле закон сохранения систем, а значит, и закон жизни всего живого на основе алгебры логики Джорджа Буля выражается логическим произведением:
![]() (4). где 1 - утверждение (жизнь), 0 - отрицание (смерть).
(4). где 1 - утверждение (жизнь), 0 - отрицание (смерть).
Это означает, что жизнь системы как целого и как части может сохраниться только при условии одновременной реализации главной и функциональной целей.
Используя параметры главной цели Аi, формулу (4) можно преобразовать в следующее логическое произведение ![]() (5)
(5)
Отсюда видно, что пренебрежение формированием какой-нибудь из этих переменных, а также невыполнение функции по отношению к вышестоящим системам ФL приведет систему к деградации. В рамках нечеткой логики формула (5) может быть записана в следующем виде: ![]() (6)
(6)
Из формулы (6) видно, что ни один из множителей не должен равняться нулю.
В реальности системы всегда находятся в промежуточных состояниях, когда присутствуют одновременно крайние противоположности, поэтому, мы предлагаем решение этой задачи в ином ключе, а именно: для естественных процессов определить доли каждой из этих противоположностей в любой момент времени и отнести состояния процессов в одну из зон: опасных, критических или оптимальных. Следует заметить, что до сих пор эта задача так не формулировалась.
Мы решаем эту задачу для систем «человек», «общество», «природа» с позиции принципа гармонии, сущность которого заключается в том, что создано природой, существует в гармонии, и только человек, устремляясь за своими желаниями, способен нарушить ее своей свободной волей.
Если рассмотреть крайние состояния некоторого процесса как полюсы, между которыми находится изучаемый процесс в данный момент, то областью гармоничных (оптимальных) состояний будет та, которая образуется границами «золотого сечения». Понятие «золотого сечения» было введено Леонардо да Винчи и использовано им как критерий гармоничности в природе, геометрии, искусстве и многих других сферах практической и умственной деятельности.
В соответствии с принципом «золотого сечения», отрезок, равный единице, делится на части в отношении 0,382/0,618 = 0,618. Используя квалиметрический подход, можно построить шкалу «пространственной изменчивости естественных процессов», в которой на основе принципа «золотого сечения» определяются зоны оптимальных состояний, риска и опасностей [4].
Для решения проблемы исследования необходимо выбрать крайние состояния главной (Г) и функциональной (Ф) целей системы и количественно описать закон сохранения систем (закон жизни) для рассматриваемого процесса - формирования готовности личности к профессиональной педагогической деятельности на основе непрерывного развития педагогической функции.
Основная трудность в решении этой задачи заключается в количественном определении значений этих целей. Для решения этой задачи мы воспользуемся параметрами А1, А2, А3, А4, А5 главной и функциональной целей Д.М. Мехонцевой. Уровень показателей параметров главной и функциональной целей любой социальной системы на данном интервале времени должен быть таким, чтобы она могла сохраняться и развиваться, значит, должны быть признаки, позволяющие оценить каждый параметр количественно.
Далее мы определили совокупность признаков, которые дают возможность оценить каждый параметр, а, следовательно, и каждую цель системы количественно.
Согласно философскому принципу дополнительности, признаки должны составлять диалектические пары. В этом случае доля признаков главной цели К1 и доля признаков функциональной цели К2 в сумме дадут единицу, а значит, можно применить метод «золотого сечения» для определения оптимальной (гармоничной) области. Откладывая К1 слева на оси, а К2 справа, можно получить точку Х, которая попадет в одну из определенных нами областей: опасную, критическую или оптимальную. По расположению Х относительно середины отрезка можно определить, какая из тенденций преобладает: наблюдается либо усиление главной цели (самосохранение человека), либо функциональной цели (сохранение общества и природы). Для человека и природы как систем состояние будет нормальным, если Х попадает в зону гармонических состояний.
В зоне гармонических состояний присутствуют обе тенденции (слева и справа от середины отрезка). Какая из них предпочтительней, определяется условиями существования систем.
Каждый естественный процесс как целое существует и развивается в совокупности полярных свойств, каждое из которых является дополнением другого до целого, но их нельзя рассматривать как «хорошие» или «плохие» [4, с. 32]. В конкретных условиях лучше применять какой-то один подход, в соответствии с «уместностью» или «неуместностью» его применения здесь и сейчас. Уместными принято считать те события, которые соответствуют некоторой норме - гармоничности.
Понятия «уместности» и «неуместности» тесно связаны с широко распространенной в философии концепцией дополнительности (подробно описана Нильсом Бором). Эти понятия конструктивно выражаются через два признака [4]:
- уместность (неуместность) выступает при анализе изменчивости естественного процесса в виде какого-то третьего компонента в дополнение к его полярным свойствам как некоторое условие существования полярности;
- природа этого третьего компонента более «тонкого» свойства;
- к процессу она относится как причина к следствию.
Изменения в этом «третьем» компоненте меняют характер текущего состояния, «делают» его «уместным» или «неуместным» с какой-то точки зрения.
Условия «уместности» или «неуместности» определяют пару полярных свойств естественного процесса, связанного с наблюдением. Они определяются из социокультурных условий и хронологических фаз.
Конкретизируя параметры главной и функциональной целей систем «человек», «общество», «природа», можно определить функциональные цели каждой из них, которые являются параметрами соответственной вышестоящей системы.
Обобщая сказанное, отметим, что развитие современного образования, в том числе и педагогического, можно представить как развитие целостной системы, в основу которой положен закон сохранения систем.
Новые проблемы человечества обусловили иные подходы к подготовке современного педагога, так как соотнесение педагогической деятельности с жизнью общества дает ключ к пониманию того, что педагогическая деятельность не только вытекает из социальной ситуации, но и ведет к ее обновлению, изменяя ее в соответствии с целями общественного развития. Кроме этого, анализ современного состояния общества показывает, что в обществе слабо сформирована одна из основных функций человеческой деятельности - педагогическая, которая является стержнем системы «человек» и помогает удерживать все остальные системы в равновесном состоянии. Таким образом, развитие педагогической функции является важнейшим фактором сохранения равновесия систем «человек», «общество», «природа».
Педагогическая функция должна развиваться непрерывно в системе педагогического образования, а значит необходимо моделирование процессов ее развития, которое позволяет рассмотреть этапы формирования готовности личности к качественному выполнению профессиональной педагогической деятельности системно и с разных позиций.
Среди множества различных моделей особую роль играют математические модели, представляющие собой приближенное описание какого-либо явления внешнего мира с помощью математической символики (рис.1).
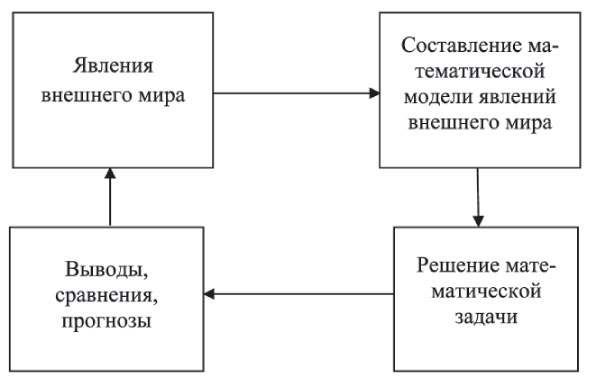
Рис. 1. Процесс математического моделирования явлений внешнего мира
Математическая модель развития педагогической функции позволяет выбрать оптимальную траекторию и наиболее эффективный путь ее развития.
Хотя математическая модель не может претендовать на получение надежных и достоверных оценок, но она может дать качественное преставление о механизмах наблюдаемых явлений и далеко не очевидных причинно-следственных связях.
Рассмотрим процесс получения педагогического образования конкретным человеком и активного развития у него педагогической функции в условиях массового обучения. Будем считать, что существует некая величина Х*, которая характеризует степень готовности личности к непрерывному развитию педагогической функции. С этого момента личность миновала стадию подготовки и готова к развитию своей педагогической функции для осуществления качественной профессиональной педагогической деятельности.
Изменение уровня готовности определяется временем, затраченным учебным заведением и самим обучающимся. Можно сказать, что это «среднее общественно необходимое время». Изменение уровня готовности со временем определяется обыкновенным дифференциальным уравнением X¢ = f(x) + I(t), x(0) = x0, (7)
|
где x - |
величина характеристики готовности личности к развитию педагогической функции; |
|
t - |
время; |
|
I(t) - |
функция, характеризующая усилие системы образования; |
|
f(x) - |
функция готовности. |
Группа ученых (С.П. Капица, С.П. Курдюмов, Г.Г. Маленицкий др.) изучала зависимость f(x) от модели образования. Если это модель «наполняемого сосуда», то f(x) = 0, I(t) = I0 при 0 ≤ t ≤ T, где T - время подготовки специалиста [3].
Применительно к развитию педагогической функции, в случае модели «зажигания огня» область допустимых значений этой функции условно может быть разделена на три участка, что соответствует развитию человека (рис. 2):
- на первом, от 0 до x0, происходит естественное развитие педагогической функции;
- на втором, от x0 до некоторой величины Х*, происходит ее развитие до планируемой величины;
- на третьем, х≥Х*, идет реализация педагогической функции в практической деятельности.
Заштрихованная площадь (x < Х*) показывает затраты на формирование готовности будущего учителя к непрерывному развитию педагогической функции, а дальше, при x > Х*, человек сам начинает развивать свою педагогическую функцию и реализовывать ее в профессиональной педагогической деятельности.
Площадь S1 зависит от способностей личности. Если личность легко воспринимает учебный материал, то затраты небольшие и отдача (площадь S1) наступает быстрее. Противоположная ситуация имеет место с плохо воспринимающей личностью, поэтому площадь S1 здесь значительно больше. Конкретная функциональная зависимость f(x) на этом этапе анализа не имеет принципиального значения.

Рис. 2. Функциональная зависимость непрерывного развития педагогической функции
Доведение личности до состояния Х* требует индивидуального подхода, так как для каждого индивида площадь S1 своя. В условиях массового обучения необходимо учитывать тот факт, что преподаватель не имеет возможности каждому уделять необходимое для него лично время выхода на требуемое состояние развития педагогической функции. Поэтому требуется оптимизация затрат усилий и времени за счет самоорганизации, а также диплом в тюмени.
Самым важным из этих этапов является второй - адаптационный. Он предполагает доведение большинства личностей от начального уровня готовности x0 на основе запуска процесса «самоорганизации» до уровня Х*, когда процесс будет необратимым. Этот этап реализуется через присутствие в каждом коллективе хорошо подготовленных к развитию педагогической функции личностей, которые при соответствующей организации учебного процесса в дальнейшем станут педагогами-профессионалами.
Адаптационный этап предполагает, что дальше процесс развития будет необратимым и может перейти в саморазвитие (этап III). Предложенная математическая модель предписывает необходимость выполнения следующих требований:
- определение исходного уровня х0 развития педагогической функции;
- проектирование технологии адаптационного периода, позволяющей перевести объект (обучающегося) из состояния х0 в состояние Х*;
- разработка диагностики определения уровня сформированности педагогической функции.
В современных научных исследованиях пока не разработан детальный механизм непрерывного развития педагогической функции в зависимости от возраста человека и социально-экономических условий.
Мы считаем необходимым разработку хронологической модели, так как развитие педагогической функции личности должно быть непрерывным и осуществляться в соответствии с хронологическими фазами развития человека.
Реализация принципов и ценностных ориентаций предполагает, с одной стороны, дифференциацию содержания процессов образования, а с другой - его концентрацию вокруг базового «ядра» способностей к самоопределению, самоорганизации в деятельности, саморазвитию. Педагогическое самоопределение уместно понимать как деятельность человека, принимающую то или иное содержание в зависимости от этапа его развития.
В хронологической модели эти хронологические фазы совмещены с принятыми в России подсистемами образования «школа - вуз - послевузовское образование». Эти подсистемы и являются основой для моделирования процессов формирования готовности личности к реализации педагогической функции в любом ее проявлении в социуме.
Из этой модели следует, что становление личности педагога - профессионала предполагает развитие педагогической функции для осуществления педагогической деятельности в любом ее проявлении в социуме и для сохранения и развития общества и природы. Непрерывность модели (рис. 3) подразумевает возможность проектирования содержания и технологий развития педагогической функции в зависимости от хронологических фаз развития человека. Влиться в этот процесс может всякий индивид на любом этапе развития педагогической функции.
Основываясь на хронологической модели развития педагогической функции, разработаем этапы развития педагогической функции в соответствии с этапами подготовки личности к профессиональной педагогической деятельности. Кроме этого, для каждой фазы здесь указаны наиболее предпочтительные направления образовательных технологий, исходя из условий «уместности», к которым мы относим социокультурные условия и возрастные особенности. На рис. 4 отображено развитие педагогической функции, разделенное на три этапа:
- Ориентация на педагогическую деятельность.
- Подготовка к педагогической деятельности как профессиональной.
- Совершенствование педагогической деятельности.
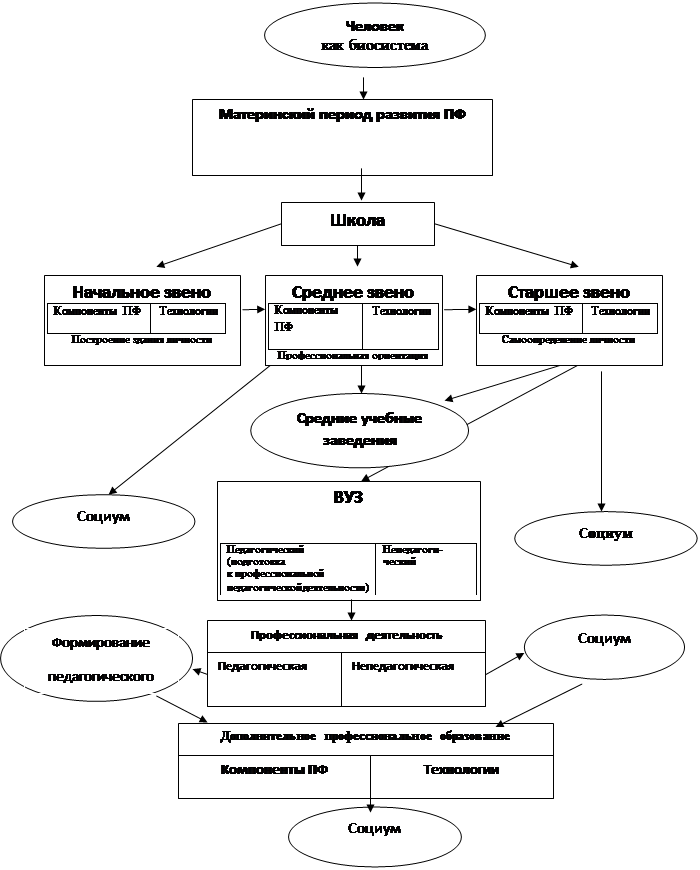
Рис. 3. Модель развития педагогической функции в системе непрерывного образования
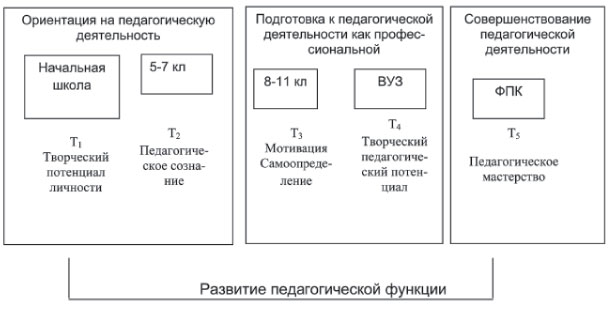
Рис. 4. Этапы подготовки личности к профессиональной педагогической деятельности на основе развития педагогической функции
Заметим, что первый этап непрерывного развития педагогической функции начинается с творческого развития личности, а это происходит особенно интенсивно в младшем школьном возрасте.
В соответствии с хронологическими фазами развития человека, следующий этап развития педагогической функции - это формирование педагогического сознания, которое является основой профессионального самоопределения личности.
Этап самоопределения личности - третья хронологическая фаза, которая не может осуществляться без мотивации. Именно на этом этапе формирования личности необходима разработка научно обоснованных педагогических технологий формирования позитивной мотивации к развитию своей педагогической функции и реализации ее в профессиональной педагогической деятельности.
На этапе подготовки личности к педагогической деятельности как профессиональной очень важным является развитие творческого педагогического потенциала, который позволяет интенсивно развивать педагогическую функцию в течение всей жизнедеятельности. На этом этапе человек должен сконцентрировать все свои возможности в процесс собственного допрофессионального и профессионального развития.
Следующий этап - это совершенствование педагогической деятельности предполагает наличие элементов педагогического мастерства в деятельности педагога-профессионала и обеспечивает дальнейшее творческое развитие педагогической функции.
Считаем нужным представить и социокультурную модель непрерывного развития педагогической функции к профессиональной педагогической деятельности, которая задает всю систему подготовки личности. Главной целью модели является организация активной познавательной деятельности для формирования определенных компонентов педагогической функции.
На наш взгляд, социокультурная модель развития педагогической функции может быть представлена следующим образом (рис. 5).
В этой модели, исходя из условий «уместности», определены стратегические направления формирования готовности человека к реализации педагогической функции в профессиональной педагогической деятельности.
Условия «уместности» определяются в соответствии с хронологическими фазами и социокультурными условиями. На каждом из выделенных этапов необходимо определить уровень готовности индивида к реализации педагогической функции в профессиональной педагогической деятельности Х* (исходя из математической модели). Следуя положениям теории самоорганизации, процесс будет необратимым, если формируемое свойство также удовлетворяет правилу «золотого сечения», то есть отношение сформированных признаков к их максимально возможному числу должно быть больше 0,67. Поэтому в качестве критерия завершенности выполнения программы каждого этапа является значение Х* > 0,67. Сами Хi* определяются для того содержания педагогической функции, которое выделено для данной хронологической фазы и социокультурных условий.
Таким образом, социокультурная модель (рис. 5) является интеграцией математического, хронологического и социокультурного направлений моделирования такого сложного естественного процесса, как непрерывное развитие педагогической функции и подготовки личности к качественному выполнению профессиональной педагогической деятельности. Недостатком этой модели является ее слишком общий характер.
Проектирование педагогических явлений обязательно должно подчиняться двум важнейшим принципам: человеческих приоритетов и саморазвития проектируемых систем [9, с. 114].
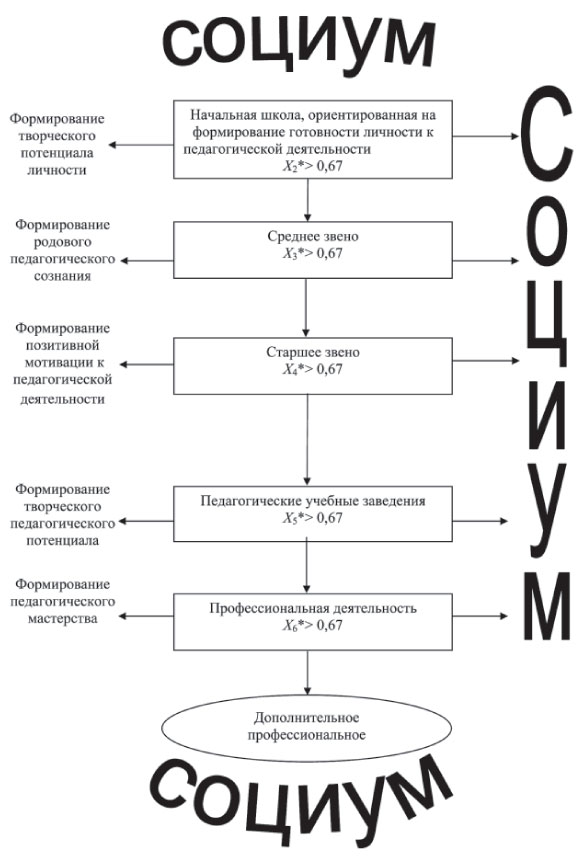
Рис.5. Социокультурная модель развития педагогической функции
Для получения эффективного проекта на основе социокультурной модели необходимо определить, что проектируется и какова должна быть структура объекта проектирования. В случае проектирования системы непрерывного развития педагогической функции мы определили ее структуру функциональными блоками: «защита», «обучение», «воспитание», «развитие», а связи между ними - через параметры главной и функциональной целей человека как системы.
Наиболее удобно установить связи между четырьмя функциональными блоками и пятью параметрами целей в виде матрицы.
Целостность проекта во взаимосвязи всех его составных частей определяется выбором системообразующего фактора, который способен объединить все другие компоненты в целостное единство и стимулировать их развитие. Таким системообразующим фактором является принцип преемственности, который способен быть основным логическим узлом в развитии процесса обучения и формулировки дидактических правил и положений.
Целезадатчиком является формирование достаточного уровня Х* готовности личности к развитию педагогической функции при оптимальном соотношении главной и функциональной целей человека как системы в соответствии с возрастными особенностями. Все вышеперечисленное реализуется в матричной модели-проекте (табл. 1), в котором на пересечении строк и столбцов стоят те признаки, которые определяют функциональные блоки педагогической функции в соответствии с параметрами целей.
Первоначально необходимо установить выполнимость диалектического принципа гармонии, для чего требуется определить количественные значения главной и функциональной целей.
Качество проектирования определяется через достижение поставленных целей. Для этого определяют показатели результатов, сравнивают их с поставленными целями и проверяют их статистическую значимость.
Построенная матричная модель дает возможность увидеть диалектические пары противоположных признаков, которые позволяют экспертам вычислить средний уровень их присутствия в каждой возрастной категории обучаемых.
Свертка показателей признаков дает интегральный показатель главной и функциональной целей, численное значение которого по шкале пространственной изменчивости процессов позволяет определить состояние исследуемого явления (опасное, критическое или гармоническое).
Если уровень Х* сформированности педагогической функции выше критического значения, то проверить текущее состояние процесса, определить тенденции его развития и принять решение о дальнейших действиях, исходя из новых социокультурных условий и принципа «уместности».
Таблица 1 Матричная модель-проект формирования функциональных блоков педагогической функции в соответствии с параметрами целей
|
Параметры целей Блоки ПФ |
А1 |
А2 |
А3 |
А4 |
А5 |
Показатели сформированности ПФ по каждому блоку |
|
Защита (З) |
|
|
|
|
|
|
|
Обучение (О) |
|
|
|
|
|
|
|
Воспитание (В) |
|
|
|
|
|
|
|
Развитие (Р) |
|
|
|
|
|
|
|
Показатели сформированности ПФ по целям |
|
|
|
|
|
|
Матричная модель, представленная в табл.1, является целезадатчиком для проектирования педагогической технологии развития педагогической функции на всех ступенях разработанной системы.
Таким образом, резюмируя представленное выше, можно отметить, что именно системно-деятельностный подход и моделирование позволяют эффективно развивать педагогическую функцию в системе непрерывного педагогического образования.