Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Жесткая В. Д., Чижиумов С. Д.,
1.2. Исключение функции потенциала движения жидкости
Исключим из уравнений (1) – (4) потенциал скорости Ф. Учтем при этом, что, применяя метод конечных элементов, мы аппроксимируем реальную ледяную пластину ее дискретной моделью, обладающей конечным числом степеней свободы; обозначим это число через n. Пользуясь известным в теории малых колебаний приемом, представим w и F в виде сумм частных решений wm, Fm системы уравнений задачи, разложив при этом Fm на два сомножителя:
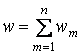, (1.5)
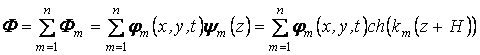. (1.6)
Здесь 
- некоторая, пока неизвестная, постоянная, а значение n, как будет указано далее, зависит от числа узлов сетки, принятой при разбиении пластины на конечные элементы, и равно количеству узловых перемещений дискретной модели пластины. Выражение для 
в правой части (1.6) получено [2] в результате подстановки 
в (2), разделения переменных и решения получившегося дифференциального уравнения с переменной z.
.
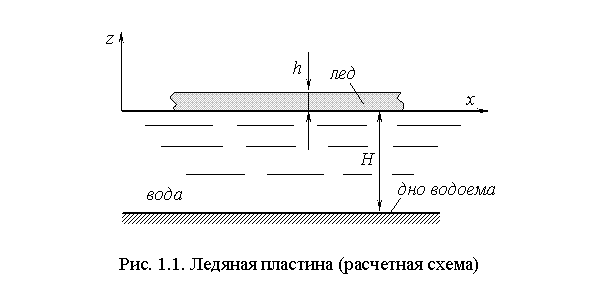Подставим (1.5) и (1.6) в уравнения (1.1) - (1.4). При этом уравнение (1.3) удовлетворяется, а уравнения (1.1), (1.2), (1.4) преобразуются к виду
.
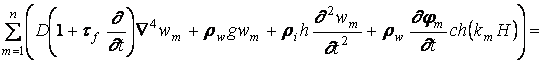, (1.7)
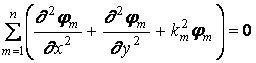, (1.8)
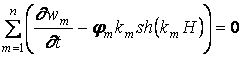. (1.9)
Исключая из (1.7), (1.8), (1.9) jm, получим систему двух уравнений
(1.10)
Если водоем ограничен вертикальными стенками, то следует рассмотреть еще условие непротекания на стенке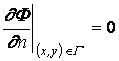 
, где нормаль n перпендикулярна оси z, Г - граница водоема.
Подставляя сюда Ф из (1.6), получим
.
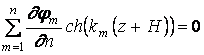и далее, учитывая (1.9),
,
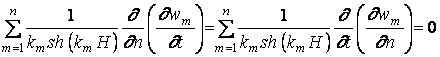откуда следует, что на границе водоема должно выполняться условие
.
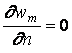