Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Численный расчет напряженно-деформированного состояния ледяного покрова, находящегося под действием нестационарной нагрузки

Жесткая В. Д., Чижиумов С. Д.,

1.4. Решение системы матричных дифференциальных уравне-ний задачи

Для решения системы (1.29) применим метод конечных разностей. Разобьем рассматриваемый промежуток времени на L равных участков; первую и вторую производные в r-м узле сетки времени аппроксимируем разностными формулами

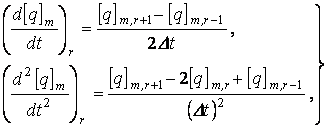(1.30)

где Dt - шаг сетки, [q]_m,r - значение вектора [q]_m в r-м узле.

Подстановка (1.30) в систему (1.29) приводит к матричным уравнениям в конечных разностях

(1.31)

r = 0,1,2,...,L ,

где

Второму уравнению системы (1.31) можно удовлетворить, представив [q]_m,r в виде

, (1.32)

где [X]_m - собственный вектор в случае однородной системы линейных уравнений с матрицей , соответствующий собственному значению , a_m,r - неизвестный коэффициент.

Подставив (1.32) в первое уравнение системы (1.31), получим:

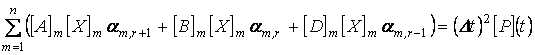, (1.33)

r = 0,1,2,....,L .

Уравнение (1.33) должно быть дополнено начальными условиями.

Пусть в начальный момент времени t=0 вектор узловых перемещений [q] был равен , а скорость его изменения - :

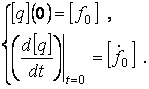(1.34)

Из (1.13), (1.30), (1.32) и (1.34) следует, что

(1.35)

Из уравнений (1.35) найдем и . Значения a_m,0 и a_m подставим в (1.33) и получим окончательный вид системы уравнений для определения a_m,r (r = 1,2,...,L):

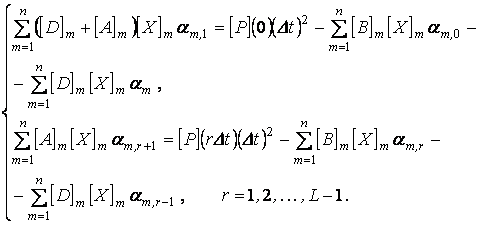(1.36)

Иногда оказывается удобным принять начальные условия в виде

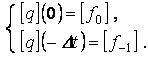(1.37)

В этом случае из (1.37) получим:

(1.38)

Определив из (1.38) a_m,0 и a_m,-1 , на основании (1.33) найдем остальные a_m,r из системы уравнений

.

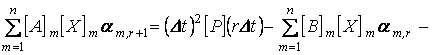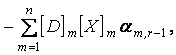r = 0,1,2,....,L-1. (1.39)

Определив из (1.36) или (1.39) a_m,r и учитывая (1.13) и (1.32), найдем узловые перемещения в узле сетки времени:

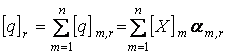. (1.40)