Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Численный расчет напряженно-деформированного состояния ледяного покрова, находящегося под действием нестационарной нагрузки

Жесткая В. Д., Чижиумов С. Д.,

1.6. Определение напряжений в точках ледяной пластины

Изгибающие и крутящий моменты, действующие в сечениях, нормальных к осям x и y, и приходящиеся на единицу длины сечения, связаны с прогибом пластины зависимостями [4]

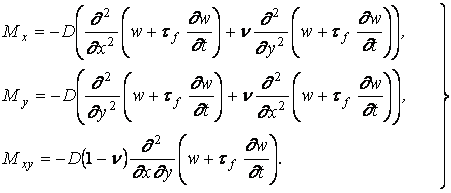(1.41)

Пусть w_r - прогиб в r-м узле сетки времени. В соответствии с (1.5) и (1.11)

.

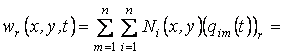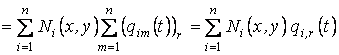, (1.42)

где q_i,r(t) - i-е узловое перемещение в r-м узле сетки времени, n - число узловых перемещений в общей системе координат.

Построим разностную схему для скорости изменения прогиба в r-м узле временной сетки. На основании (1.42), используя разностную формулу первой производной, получим:

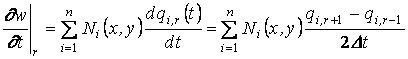. (1.43)

Здесь, на основании (1.40),

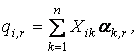(1.44)

где X_ik (i = 1, 2,...., n) - элементы вектора X_k :

.

Внеся (1.43) в (1.41), получим:

,

,

.

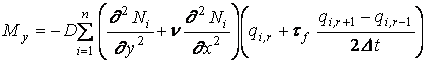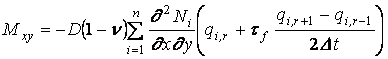Обозначим

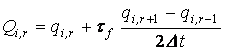. (1.45)

Подставив в (1.45) согласно (1.44), получим

.

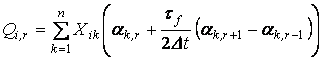Формулы моментов после введения обозначения (1.45) примут вид

(1.46)

Найдя М_x , M_y и M_xy , вычислим наибольшие нормальные s_{x max} ,
s_{y max} и наибольшее касательное t_{xy max} напряжения. Соответствующие величины, , для частного случая изотропной пластины определяются по формулам:

.

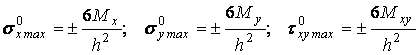Процедура определения напряжений в точках конечного элемента ледяной пластины в r-м узле сетки времени выглядит следующим образом:

a) вычисляются , т.е. выполняется (r+1)-й шаг по времени; при этом сохраняются найденные на двух предыдущих шагах и ;

б) вычисляется вектор в общей системе координат, т.е. для всей пластины:

;

в) из элементов последнего формируется вектор [Q]_r в местной системе координат, т.е. для отдельного конечного элемента с числом узловых перемещений ne:

;

г) по формулам (1.46) определяются моменты M_x , M_y , M_xy в заданных точках конечного элемента;

д) вычисляются наибольшие значения напряжений s_x , s_y , t_xy в заданных точках конечного элемента.