
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.2. Расчет напряженно-деформированного состояния ледяного покрова при движении нагрузки по синусоидальной траектории
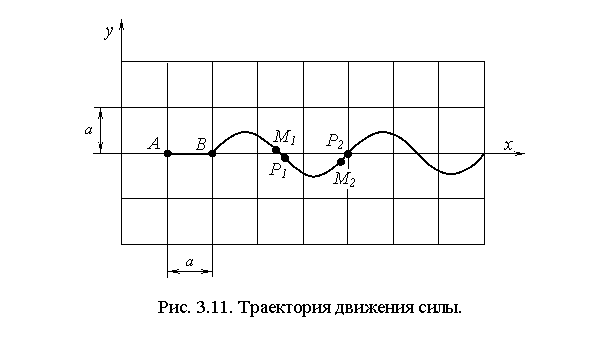
Пусть сосредоточенная сила движется по сплошному ледяному покрову. При этом сохраняются условия задачи 1 (п. 3.1.1), кроме закона движения нагрузки. Теперь Р начинает движение от точки А (в этот момент, как и в задаче 1, ледяная пластина имеет статический прогиб) вдоль оси x с постоянным ускорением, через t0 = 25 с достигает точки В, приобретя скорость v = 4 м/с, и продолжает движение по криволинейной траектории (синусоиде) 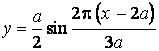 с постоянной скоростью v (рис. 3.11).
с постоянной скоростью v (рис. 3.11).
 .
.
Для решения задачи, а именно, для формирования свободного члена в уравнениях (1.36) или (1.39) необходимо предварительно определить координаты точки приложения силы Р в данный момент времени.
Приведем соответствующие зависимости для того периода времени, когда сила Р находится на синусоидальном участке своей траектории движения. Запишем уравнение синусоиды в виде
![]() , (3.1)
, (3.1)
где А - амплитуда, с - длина полуволны синусоиды, x0 – абсцисса начала синусоиды (точки В).
Пусть ![]() - известные координаты точки приложения Р после (j-1)-го шага по времени,
- известные координаты точки приложения Р после (j-1)-го шага по времени, ![]() - приращения координат на j-м шаге,
- приращения координат на j-м шаге, ![]() - координаты точки приложения Р после j-го шага. Можно показать, что
- координаты точки приложения Р после j-го шага. Можно показать, что
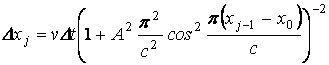 .
.
Вычислив Dxj , найдем xj = xj+1 + Dxj , а затем из (3.1)
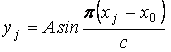 .
.
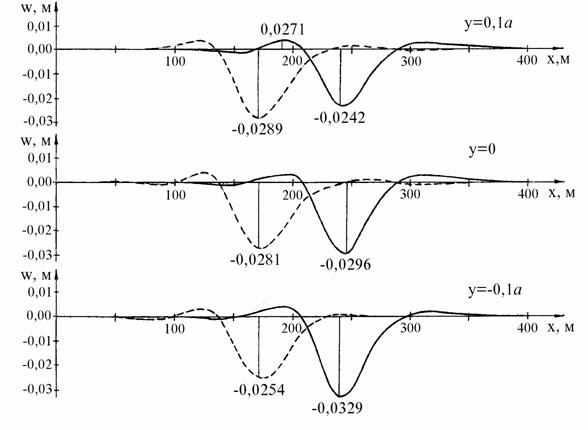
На рис. 3.12 даны построенные по результатам счета графики прогибов при y = 0,1a, y = 0, y = - 0,1a в моменты прохождения силы Р через точки Р1 и Р2 .
 .
.
Рис. 3.12. Графики прогибов.
- - - - - - сила Р находится в точке Р1
¾¾¾¾¾ сила Р находится в точке Р2
Максимальный прогиб возникает в первом случае в точке М1 с координатами x = 3,4a, y = 0,1a; во втором - в точке М2 с координатами x = 4,8a, y = - 0,15a (см. рис. 3.11).
Сравнивая наибольшие значения прогибов при движении нагрузки по прямой линии (задача 1, п. 3.1) и по синусоидальной траектории, можно заметить, что во втором случае прогибы несколько больше. Такой эффект был замечен на практике при ломке льда с помощью СВП.
По результатам счета построены также эпюры напряжений ![]() ,
, ![]() ,
, ![]() , возникающих в ледяном покрове в момент прохождения силой Р точки Р2 (рис. 3.13 - 3.15, где эти напряжения обозначены, соответственно, через sx, sy, txy).
, возникающих в ледяном покрове в момент прохождения силой Р точки Р2 (рис. 3.13 - 3.15, где эти напряжения обозначены, соответственно, через sx, sy, txy).
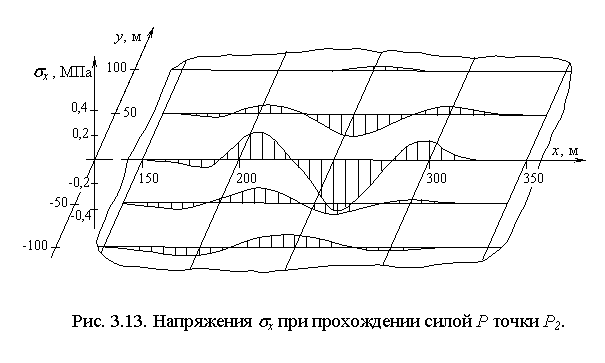 .
.
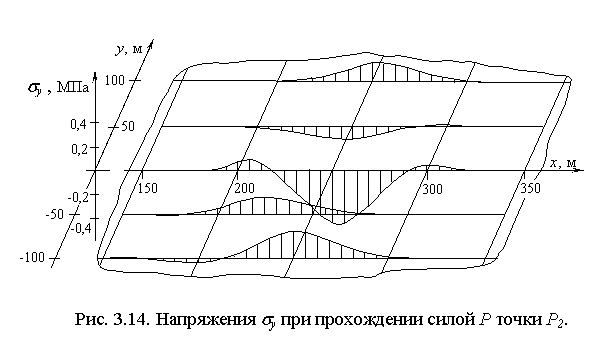 .
.
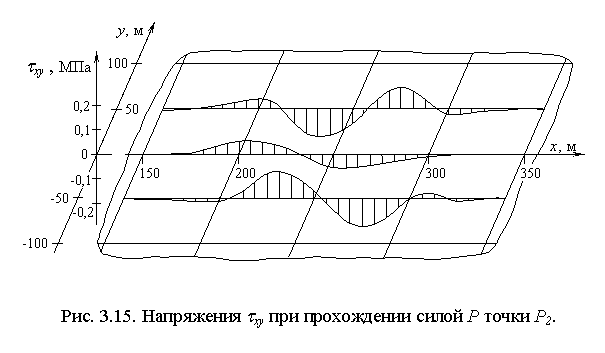 .
.
