
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ ОБСЛЕДОВАНИЯ АВТОМОБИЛЬНЫХ ДОРОГ В РАЙОНАХ ЛЕСОЗАГОТОВОК
Лобанов Ю. В., Кондрашова Е. В., Курьянов В. К.,
3.1 Теоретические основы и методика метрологических испытаний лаборатории в плане дороги
Проведение метрологических испытаний информационно-измерительного комплексам дорожной лаборатории требует разработки теоретических основ и методики их выполнения.
В качестве основного метода исследования точности принят метод сравнения результатов, полученных с его помощью, с аналогичными результатами, полученными на основе геодезических измерений. При этом геодезические данные приняты за основные, поскольку они обладают наиболее высокой точностью. Вместе с тем исследование точности дорожной лаборатории путём сравнения результатов, вычисленных при разном числе наблюдений (проездов лаборатории) также позволяет получать ряд ценных выводов, основанных на внутренней сходимости этих данных.
Решение задачи рассмотрим раздельно в плане и в продольном профиле.
Чтобы можно использовать ходовую лабораторию для съёмки плана автомобильной дороги значительной протяжённости необходимо выполнение двух условий:
1. Лаборатория должна обеспечивать измерение азимутов направлений или углов поворота оси дороги с достаточно высокой точностью (порядка нескольких угловых минут);
2. Лаборатория должна обеспечивать измерение расстояния с точностью не ниже 1/5000.
Например, при измерении азимутов или углов поворота с погрешностью ±10 и расстояний с относительной погрешностью =1/5000 положение точки в плане на оси дороги, имеющей не более одного угла поворота, через 10 км будет характеризоваться средней квадратической погрешностью, примерно равной
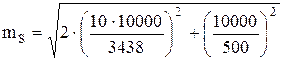 =45 м.
=45 м.
На планах масштаба 1:5000 этой величине соответствует 9 мм, а на планах масштаба 1:10000 - 5 мм. Эти погрешности, по-видимому, находятся на границе допустимых значений. Детальное рассмотрение вопроса о необходимой точности, которую должна обеспечивать лаборатория при съёмках автомобильных дорог в плане, может быть сделано в специальном исследовании.
Погрешность измерения азимутов или углов поворота с помощью дорожной лаборатории слагается из погрешностей отсчитывания по гирополукомпасу ( ![]() ) в начале и в конце закругления и погрешностей совмещения оси автомобиля лаборатории с осями прямолинейных участков дороги до начала и после конца закругления (
) в начале и в конце закругления и погрешностей совмещения оси автомобиля лаборатории с осями прямолинейных участков дороги до начала и после конца закругления (![]() ). Так как погрешности
). Так как погрешности ![]() и
и ![]() имеет случайный характер, то погрешность измерения углов поворота
имеет случайный характер, то погрешность измерения углов поворота ![]() будет равна
будет равна
![]() . (3.1)
. (3.1)
Погрешность отсчитывания по гирополукомпасу не превышает ±30. Погрешность же совмещения оси автомобиля с осями прямолинейных участков дороги до начала и после конца закругления может достигать нескольких градусов. Среднее квадратическое значение погрешности ![]() , а также закон распределения погрешностей совмещения оси автомобиля с осями прямолинейных участков дороги до начала и после конца закругления можно определить на основе следующих метрологических испытаний.
, а также закон распределения погрешностей совмещения оси автомобиля с осями прямолинейных участков дороги до начала и после конца закругления можно определить на основе следующих метрологических испытаний.
На закруглении автомобильной дороги определяют положение точек: НЗ (начало закругления) и КЗ (конец закругления). Наиболее точна задача решается геодезическим методом, описанным ниже. Автомобиль дорожной лаборатории подъезжает к точке НЗ со стороны прямолинейного участка дороги и водитель визуально совмещает его ось с осью прямолинейного участка дороги или линией, ей параллельной.
Запускают гироплукомпас и определяют: азимут начального направления ![]() . Дорожная лаборатория начинает движение по закруглению и заканчивает его за точкой КЗ на прямолинейном участке дороги. После остановки автомобиля по гирополукомпасу определяют азимут конечного направления его движения
. Дорожная лаборатория начинает движение по закруглению и заканчивает его за точкой КЗ на прямолинейном участке дороги. После остановки автомобиля по гирополукомпасу определяют азимут конечного направления его движения ![]() . Угол поворота оси дороги вычисляют по формуле
. Угол поворота оси дороги вычисляют по формуле
![]()
при правом угле поворота или по формуле
![]()
при левом угле поворота.
Далее водитель разворачивает автомобиль в обратном направлении и вновь повторяет весь путь, стараясь держать ось автомобиля до начала и после конца закругления по оси прямолинейных участков дороги. Описанные челночные проезды дорожной лаборатории по закруглению между точками НЗ и КЗ необходимо повторить примерно 25 раз, чтобы иметь достаточное число значения ![]() .
.
Статистическая обработка результатов испытаний состоит в следующем:
1. вычисляют среднее значение угла поворота ![]()
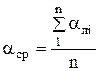 ;
;
2. Вычисляют среднюю квадратическую погрешность одного определения ![]()
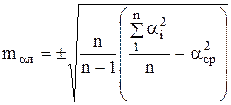 (3.2)
(3.2)
и среднего значения ![]()
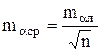 ; (3.3)
; (3.3)
3. Существуют основания полагать, что распределением величины ![]() и её погрешности
и её погрешности ![]() не противоречат нормальному закону (это утверждение можно проверить с помощью критериев согласия или другим простым методом).
не противоречат нормальному закону (это утверждение можно проверить с помощью критериев согласия или другим простым методом).
В связи с этим можно построить доверительные интервалы для истинного угла поворота ![]() по результатам одного i-го проезда лаборатория и по осредненным данным на n проездов:
по результатам одного i-го проезда лаборатория и по осредненным данным на n проездов:
![]() , (3.4)
, (3.4)
![]() , (3.5)
, (3.5)
где t - квантиль нормированного нормального распределения, соответствующий принятой вероятности ![]() .
.
Чтобы выяснить, насколько устойчиво значение ![]() при различном числе проездов лаборатории по закруглению, и как зависит погрешность
при различном числе проездов лаборатории по закруглению, и как зависит погрешность ![]() от числа проездов n, необходимо повторить все вычисления по
от числа проездов n, необходимо повторить все вычисления по ![]() проездов. Для этого все результаты необходимо разделить на четные и нечетные и вычислять все статистики отдельно по четным и нечетным значениям. Аналогично необходимо образовать выборки из 1,4,7,10,..., затем из 2,5,8,11,...и 3,6,9,12,..., значения
проездов. Для этого все результаты необходимо разделить на четные и нечетные и вычислять все статистики отдельно по четным и нечетным значениям. Аналогично необходимо образовать выборки из 1,4,7,10,..., затем из 2,5,8,11,...и 3,6,9,12,..., значения ![]() (то есть отобрать из всех значений каждый третий результат, начиная с первого, затем со второго и затем с третьего) и повторить трижды вычисления всех статистик по 1/3 всех проездов. Аналогичным образом необходимо образовать 4 выборки численностью
(то есть отобрать из всех значений каждый третий результат, начиная с первого, затем со второго и затем с третьего) и повторить трижды вычисления всех статистик по 1/3 всех проездов. Аналогичным образом необходимо образовать 4 выборки численностью ![]() и вновь повторить все вычисления.
и вновь повторить все вычисления.
Результаты всех вычислений можно представить на графиках. Если на графике провести горизонтальную прямую на уровне ![]() (
( ![]() - допустимое значение погрешности
- допустимое значение погрешности ![]() ), то на оси абсцисс можно получить значение n, которое обеспечивает определение
), то на оси абсцисс можно получить значение n, которое обеспечивает определение ![]() с допустимой погрешностью. Величина n определяет необходимое число челночных проездов дорожной лаборатории по закруглению, по данным которых определяют среднее значение угла поворота
с допустимой погрешностью. Величина n определяет необходимое число челночных проездов дорожной лаборатории по закруглению, по данным которых определяют среднее значение угла поворота ![]() с погрешностью, не более
с погрешностью, не более ![]() .
.
Из изложенного можно видеть, что основной погрешностью, определяющей точность измерения угла поворота ![]() с помощью дорожной лаборатории, является погрешность совмещения оси автомобиля (точнее, линии начального отсчёта гирополукомпаса) с осью прямолинейного участка дороги (или линией, ей параллельной), перед началом и после конца закругления дороги. Эта погрешность в несколько раз превосходит погрешность отсчитывания по гирополукомпасу, поэтому погрешность измерения угла поворота почти полностью определяется величиной погрешности
с помощью дорожной лаборатории, является погрешность совмещения оси автомобиля (точнее, линии начального отсчёта гирополукомпаса) с осью прямолинейного участка дороги (или линией, ей параллельной), перед началом и после конца закругления дороги. Эта погрешность в несколько раз превосходит погрешность отсчитывания по гирополукомпасу, поэтому погрешность измерения угла поворота почти полностью определяется величиной погрешности ![]() .
.
Соотношения (3.2), (3.3), (3.4), (3.5) позволяют оценить точность определения угла поворота, однако они же являются полным и окончательным решением задачи. Как указывалось, наиболее полные и достоверные оценки метрологических характеристик дорожной лаборатории можно получить из сравнения угловых и линейных величин, полученных с его помощью, с соответствующими величинами, полученными на основе геодезических измерений. Ниже рассматриваются теоретические основы и методика сравнения указанных данных.
Для сравнения углов поворота, полученных с помощью дорожной лаборатории ( ![]() ) и на основе геодезических измерений (
) и на основе геодезических измерений ( ![]() ), на закруглении необходимо определить точки НЗ и КЗ. Если закругление состоит полностью из круговой кривой, то это будут точки НК и КК. Если же в конструкции закругления имеются переходные кривые, то это будут точки НПК (начало переходной кривой). В последнем случае на закруглении необходимо выделить НК и КК круговой кривой, так как все изложенное ниже относится к методике метрологических испытаний лаборатории на круговых кривых.
), на закруглении необходимо определить точки НЗ и КЗ. Если закругление состоит полностью из круговой кривой, то это будут точки НК и КК. Если же в конструкции закругления имеются переходные кривые, то это будут точки НПК (начало переходной кривой). В последнем случае на закруглении необходимо выделить НК и КК круговой кривой, так как все изложенное ниже относится к методике метрологических испытаний лаборатории на круговых кривых.
Точку НЗ определяем с помощью теодолита. Для этого в точке N на кромке покрытия устанавливают теодолит, а в точке M (то же на кромке покрытия) устанавливают веху. Визируют на веху М и трубу переводят через зенит. Речник А начинает двигаться от теодолита N в сторону середины закругления. В момент, когда рейка начинает смещаться с перекрестия сетки трубы, точку фиксируют на кромке покрытия. Аналогичным образом фиксируют точки при движении речника А в сторону от середины закругления к теодолиту. Расстояние между полученными точками делят пополам и построенную таким образом точку принимают за НЗ (НК. Для повышения точности решения задачи наблюдения рекомендуется производить при КП и КЛ.
Точки M,N и А необходимо выбирать на кромке покрытия тщательно, с учётом следующих соображений. Кромка покрытия не является идеальной линией, точно совпадающей с круговой кривой закругления. Её отклонения от указанных кривых обусловлены погрешностями разбивки оси и проезжей части закругления, погрешностями строительных работ и, наконец, разрушением и загрязнением при эксплуатации дороги.
Погрешности разбивки оси дороги на закруглении связаны с тем, что плавная круговая кривая заменяется хордами длиною S=10,15,20 м. Середины хорд отклоняются от круговой кривой на величину «стрелы» ![]() , которая проявляет себя как погрешность разбивочных работ. Из табл. 3.1 видно, что при хордах S=10 и 20 м стрелы f в зависимости от радиуса круговой кривой изменяются в широких пределах.
, которая проявляет себя как погрешность разбивочных работ. Из табл. 3.1 видно, что при хордах S=10 и 20 м стрелы f в зависимости от радиуса круговой кривой изменяются в широких пределах.
Если полагать, что при хордах ![]() м точки оси дороги разбивают также и от их середин построением перпендикуляров длиною
м точки оси дороги разбивают также и от их середин построением перпендикуляров длиною ![]() (
( ![]() - угол, соответствующий хорде S), то погрешности разбивки оси при
- угол, соответствующий хорде S), то погрешности разбивки оси при ![]() м не выйдут за пределы 6,5 см.
м не выйдут за пределы 6,5 см.
Допускаемые проектные отклонения от проектных размеров ширины покрытия равны: для асфальтобетонных покрытий ![]() СМИ для цементобетонных
СМИ для цементобетонных ![]() см.
см.
Таблица 3.1 - Зависимость величин f от радиуса кривой R
|
Радиус круговой кривой R, м |
Стрела f, см |
|
|
При S=10 м |
При S=20 м |
|
|
1000 |
1,2 |
5,0 |
|
800 |
1,6 |
6,3 |
|
600 |
2,1 |
8,3 |
|
400 |
3,1 |
12,5 |
|
200 |
6,3 |
25,0 |
|
100 |
12,5 |
50,0 |
Погрешность положения кромки составит при этом соответственно ![]() 7 и
7 и ![]() 3,5 см.
3,5 см.
Погрешность положения кромки, связанные с её загрязнением и разрушением при эксплуатации оценивается величиной 2-3 до 20-25 см [25]. В среднем она, по-видимому, не превышает 10-11 см.
Таким образом, суммарная величина случайного отклонения кромки покрытия от круговой кривой будет равна
![]() см.
см.
Если погрешность ![]() см считать предельной, то средняя (квадратическая) будет равна
см считать предельной, то средняя (квадратическая) будет равна ![]() см. Естественно, значения 1 весьма существенно зависит от качества строительных работ, типа покрытия, и на дорогах разных категорий может различаться значительно. Ниже изложена методика определения значения 1 для каждого конкретного закругления.
см. Естественно, значения 1 весьма существенно зависит от качества строительных работ, типа покрытия, и на дорогах разных категорий может различаться значительно. Ниже изложена методика определения значения 1 для каждого конкретного закругления.
Для уменьшения искажающего влияния величины 1 на точность и надёжность определения точек НЗ и КЗ на закруглении рекомендуется следующий приём. В местах разметки точек M и N, а также установки рейки А на кромке проезжей покрытия провести мелом огибающие линии по выступам и впадинам извилин кромки и в полученном «коридоре», на осевой его линии, разметить указанные точки (рис. 8.3). Таким путём достигается выравнивание линии кромки покрытия и приближение её к идеальной кривой закругления.
Для определения возможно более точного значения угла поворота оси дороги необходимо произвести его измерение теодолитом. С этой целью на кромке покрытия, примерно на середине закругления устанавливают теодолит и измеряют угол ![]() при КП и КЛ. Среднее значение - это среднее арифметическое, принимают за окончательное значение угла
при КП и КЛ. Среднее значение - это среднее арифметическое, принимают за окончательное значение угла ![]() .
.
Угол поворота оси дороги, полученный измерением с помощью теодолита, равен ![]() . При этом выбор точки, в которой следует устанавливать теодолит при измерении
. При этом выбор точки, в которой следует устанавливать теодолит при измерении ![]() , не оказывает влияния на его величину, так как вершина угла всегда остаётся на кривой, а сам угол будет опираться на одну и ту же хорду АС. С этой точки зрения для измерения угла
, не оказывает влияния на его величину, так как вершина угла всегда остаётся на кривой, а сам угол будет опираться на одну и ту же хорду АС. С этой точки зрения для измерения угла ![]() не требуется точного определения положения середины закругления. Вполне достаточно для установки теодолита эту точку определить на глаз или даже выбрать произвольно.
не требуется точного определения положения середины закругления. Вполне достаточно для установки теодолита эту точку определить на глаз или даже выбрать произвольно.
Вместе с тем погрешности определения положений точек НЗ и КЗ на закруглении, а также отклонения кромки покрытия от идеальной круговой кривой на закруглении и от прямых линий на прямолинейных участках дороги (до точки НЗ и после точки КЗ) весьма существенно влияют на точность измерения угла ![]() . Поэтому при установке вешек в точках НЗ и КЗ, а также теодолита в точке СК необходимо, как указано выше, провести мелом огибающие по выступам и впадинам линии кромки покрытия и на осевых линиях этих «коридоров» окончательно выбрать точки НЗ, СЗ, КЗ.
. Поэтому при установке вешек в точках НЗ и КЗ, а также теодолита в точке СК необходимо, как указано выше, провести мелом огибающие по выступам и впадинам линии кромки покрытия и на осевых линиях этих «коридоров» окончательно выбрать точки НЗ, СЗ, КЗ.
Угол поворота ![]() можно получить также, если в точках НЗ, СЗ и КЗ измерить соответственно углы
можно получить также, если в точках НЗ, СЗ и КЗ измерить соответственно углы ![]() ,
, ![]() . Углы
. Углы ![]() в точках НЗ и КЗ можно измерить следующим образом. В точке НЗ устанавливают теодолит и приводят его в рабочее положение. На расстоянии 40-60 м от точки НЗ на прямолинейном участке дороги (на кромке покрытия) устанавливают вешку. Трубу теодолита при КП наводят на эту вешку и берут отсчёт по горизонтальному кругу. Затем трубу переводят через зенит, наводят на точку СК и берут отсчёт по тому же кругу. Разность отсчётов даёт угол
в точках НЗ и КЗ можно измерить следующим образом. В точке НЗ устанавливают теодолит и приводят его в рабочее положение. На расстоянии 40-60 м от точки НЗ на прямолинейном участке дороги (на кромке покрытия) устанавливают вешку. Трубу теодолита при КП наводят на эту вешку и берут отсчёт по горизонтальному кругу. Затем трубу переводят через зенит, наводят на точку СК и берут отсчёт по тому же кругу. Разность отсчётов даёт угол ![]() . Далее угол
. Далее угол ![]() измеряют повторно при КЛ. Аналогично измеряют угол
измеряют повторно при КЛ. Аналогично измеряют угол ![]() в точке КЗ.
в точке КЗ.
Контроль: должно выполняться условие ![]() , то есть удвоенное значение угла
, то есть удвоенное значение угла ![]() , измеренного в точке СЗ, должно быть равно сумме углов, измеренных в точках НЗ, СЗ, КЗ. Так как углы
, измеренного в точке СЗ, должно быть равно сумме углов, измеренных в точках НЗ, СЗ, КЗ. Так как углы ![]() и
и ![]() измеряются с некоторыми погрешностями, то поставленное условие почти никогда не будет выполняться строго. Несоответствие левой и правой частей условия не должно превышать примерно величины
измеряются с некоторыми погрешностями, то поставленное условие почти никогда не будет выполняться строго. Несоответствие левой и правой частей условия не должно превышать примерно величины ![]() , где
, где ![]() =3438 радиан в минутах; 1 - предельное значение величины отклонения кромки покрытия от круговой кривой (м) с вероятностью 0,7; b - средняя длина сторон, образующих углы
=3438 радиан в минутах; 1 - предельное значение величины отклонения кромки покрытия от круговой кривой (м) с вероятностью 0,7; b - средняя длина сторон, образующих углы ![]() и
и ![]() в точках НЗ, СЗ, КЗ.
в точках НЗ, СЗ, КЗ.
Например, при 1=0,05 м и b=50м эта величина будет равна 7-8.
Погрешность угла поворота, измеренного с помощью дорожной лаборатории, можно охарактеризовать разностью
![]() , где
, где ![]() и
и ![]() - значения угла поворота, полученные лабораторией и геодезическим методом.
- значения угла поворота, полученные лабораторией и геодезическим методом.
Вместе с тем разность ![]() есть результат действия случайных погрешностей при измерениях
есть результат действия случайных погрешностей при измерениях ![]() и
и ![]() , то есть
, то есть
![]() , (3.6)
, (3.6)
Откуда погрешность измерения угла поворота с помощью дорожной лаборатории будет равна
![]() . (3.7)
. (3.7)
Погрешность измерения угла теодолитом очень мало зависит от инструментальной погрешности и почти полностью определяется влиянием погрешностей положения точек НЗ и КЗ, а также отклонениями кромки покрытия на закруглении от идеальной круговой кривой. При этом отклонение кромки от указанной кривой влияют на точность измерения угла ![]() . Так же, как погрешность центрирования теодолита и наблюдаемых точек (сигналов).
. Так же, как погрешность центрирования теодолита и наблюдаемых точек (сигналов).
Влияние погрешностей центрирования теодолита и сигналов на точность измерения угла ![]() выражается формулой
выражается формулой
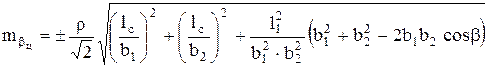 , где
, где ![]() ,
, ![]() - погрешности центрирования сигналов и теодолита;
- погрешности центрирования сигналов и теодолита; ![]() ,
, ![]() - длины сторон, образующих угол
- длины сторон, образующих угол ![]() .
.
Если ![]() ,
, ![]() и
и ![]() , то
, то ![]() .
.
Так как ![]() , то погрешность измерения угла
, то погрешность измерения угла ![]() , обусловленная отклонением кромки покрытия от круговой кривой, будет равна
, обусловленная отклонением кромки покрытия от круговой кривой, будет равна ![]() . (3.8)
. (3.8)
В формулу (3.8) входит величина 1, предельное значение которой с заданной вероятностью можно определит на основе следующих исследований. На кромке покрытия на закруглении разбивают через каждые 1-2 точки и мелом проводят в этих местах огибающие по выступам и впадинами извилистой линии кромки . С помощью сантиметровой линейки измеряют ширину построенного «коридора» около каждой точки и делят её пополам. Полученные значения 1 заносят в соответствующие классы таблицы распределения (табл. 3.2). Далее подсчитывают численности и частости классов. Чтобы определить предельное значение 1 с заданной вероятностью, в графе «частость класса» подсчитывают нарастающим итогом частости классов, начиная с самого верхнего. Известно, что при нормальном законе распределения погрешностей средняя квадратическая погрешность m имеет вероятность 0,684. В связи с этим предельное отклонение 1, имеющее вероятность ~0,68, будет соответствовать среднеквадратическую значению.
Чтобы определить предельное значение величины 1 с вероятностью ~0,68, необходимо в графе «частость класса» подсчитать нарастающим итогом сумму частостей, равную~68 %. Среднее значение 1 в классе, частость которого дополняет сумму частостей предыдущих классов до 68 % и будет равно предельному значению её с вероятностью 0,68.
8,5+17,8+30,3=56,3%. Так как частость 16,3 % в классе (3-4) дополняют сумму 56,3 % до 72,9 % (которая наиболее близка к 68 %), то предельное значение 1 с вероятностью ~0,7 будет равно примерно 3-3,5 см.
Таблица 3.2 - Таблица распределения значения
|
Классы значений 1, см от-до |
Численность класса n |
Частость класса, % |
|
0-1 |
11 |
8,5 |
|
1-2 |
23 |
17,8 |
|
2-3 |
39 |
30,3 |
|
3-4 |
21 |
16,3 |
|
4-5 |
14 |
10,8 |
|
5-6 |
9 |
7,0 |
|
6-7 |
7 |
5,4 |
|
7-8 |
5 |
3,9 |
|
Сумма |
129 |
100 |
Число значений 1, измеренных на кромке покрытия закругления, должно быть достаточно большим (![]() ).
).
Рассмотрим влияние погрешностей определения положения точек НЗ и КЗ на кривой закругления на точность измерения угла ![]() . Как показано в работе [24], влияние указанных погрешностей на точность измерения угла
. Как показано в работе [24], влияние указанных погрешностей на точность измерения угла ![]() определяется формулой
определяется формулой
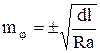 , где
, где ![]() - погрешность измерения угла
- погрешность измерения угла ![]() , обусловленная погрешностями положения точек НЗ и КЗ на закруглении;
, обусловленная погрешностями положения точек НЗ и КЗ на закруглении; ![]() - радиан в минутах; 1 - предельное отклонение кромки покрытия от круговой кривой с вероятностью 0,68;
- радиан в минутах; 1 - предельное отклонение кромки покрытия от круговой кривой с вероятностью 0,68; ![]() - расстояния; R - радиус круговой кривой.
- расстояния; R - радиус круговой кривой.
Так как ![]() , то
, то 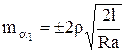 . (3.9)
. (3.9)
Суммарное влияние погрешностей ![]() и
и ![]() на точность измерения угла
на точность измерения угла ![]() будет равно
будет равно
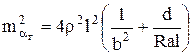 (3.10)
(3.10)
Подставляя значение ![]() в (8.7), получим
в (8.7), получим
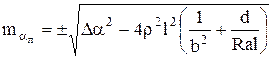 (3.11) где
(3.11) где ![]() - разность значений угла поворота оси дороги, измеренных дорожной лабораторией и теодолитом; остальные обозначения прежние.
- разность значений угла поворота оси дороги, измеренных дорожной лабораторией и теодолитом; остальные обозначения прежние.
Формула (3.11) является окончательной рабочей. Она позволяет оценивать точность измерения углов поворота ![]() оси дороги на закруглениях с помощью дорожной лаборатории. При этом разность
оси дороги на закруглениях с помощью дорожной лаборатории. При этом разность ![]() можно вычислять по значениям
можно вычислять по значениям ![]() , полученным из одного, двух, трёх, четырёх и т.п. проездов лаборатории. Таким путём можно проследить, как изменяется погрешность
, полученным из одного, двух, трёх, четырёх и т.п. проездов лаборатории. Таким путём можно проследить, как изменяется погрешность ![]() в зависимости от осреднения результатов (количества челночных проездов) и определять оптимальное число проездов.
в зависимости от осреднения результатов (количества челночных проездов) и определять оптимальное число проездов.
Анализ данных, полученных по формуле (3.11), необходимо проводить совместно с анализом данных, полученных по формулам (3.2), (3.3), (3.4) и (3.5).
Точность измерения длины круговой кривой с помощью дорожной лаборатории может быть определена следующим образом.
После установления положения точек НЗ и КЗ измеряют с помощью оптического дальномера длину кривой закругления между этими точками. Длину кривой можно вычислить также по формуле
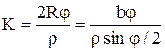 . (3.12) где
. (3.12) где ![]() .
.
Равенство длины кривой, полученной измерением дальномером, и вычисленной по формуле (3.12), может служить контролем и оценкой точности результатов геодезических измерений.
Если продифференцировать выражение (3.12) и перейти к средним квадратическим погрешностям, то погрешность определения длины кривой по (3.12) будет 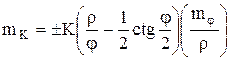 , где
, где ![]() , с вероятностью 0,95 разность между непосредственно измеренным и вычисленным значениями длины кривой не должна превышать
, с вероятностью 0,95 разность между непосредственно измеренным и вычисленным значениями длины кривой не должна превышать ![]() .
.
Далее измеряют длину кривой закругления с помощью дорожной лаборатории. Погрешность измерения длины кривой с помощью дорожной лаборатории можно охарактеризовать разностью ![]() где
где ![]() и
и ![]() - длина кривой, измеренная с помощью лаборатории и геодезическим методом.
- длина кривой, измеренная с помощью лаборатории и геодезическим методом.
Одновременно разность ![]() равна
равна ![]() . (3.13)
. (3.13)
В работе [24] показано, что погрешность измерения длины кривой, обусловленная неточным определением положения точек НЗ и КЗ, равна 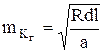 , (3.14) где R - радиус круговой кривой; d, a - расстояния; 1 - предельное отклонение кромки покрытия от круговой кривой с вероятностью ~0,68.
, (3.14) где R - радиус круговой кривой; d, a - расстояния; 1 - предельное отклонение кромки покрытия от круговой кривой с вероятностью ~0,68.
Из формулы (3.14) видно, что для уменьшения погрешности измерения длины кривой точку N (рис. 3.3) при определении начала и конца закругления следует выбирать как можно ближе к началу закругления, а расстояние ![]() достаточно большим, чтобы отношение
достаточно большим, чтобы отношение ![]() мало отличалось от единицы. Эта рекомендация была уже сформулирована раньше без специального доказательства. Указанное, естественно, относится и к выбору точек M, N в конце закругления.
мало отличалось от единицы. Эта рекомендация была уже сформулирована раньше без специального доказательства. Указанное, естественно, относится и к выбору точек M, N в конце закругления.
Подставляя из (3.14) в (3.13) значения ![]() , получим
, получим
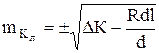 . (3.15)
. (3.15)
Формула (3.15) является рабочей и позволяет оценивать точность определения длины кривой закругления с помощью дорожной лаборатории. Как видно из предыдущего, погрешность при измерении длины кривой с помощью дорожной лаборатории в основном определяется погрешностями положения точек НЗ и КЗ на закруглении. При проездах лаборатории «туда-обратно» по закруглению можно получить среднее значение длины кривой, которое будет в ![]() раз точнее единичного определения этой длины на каждого проезда.
раз точнее единичного определения этой длины на каждого проезда.
Погрешность среднего значения кривой можно вычислить по формуле
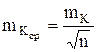 , (3.16) где
, (3.16) где 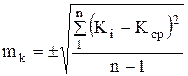 , (3.17)
, (3.17) 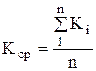 .
.
С помощью формул (3.16), (3.17) можно построить доверительные интервалы для истинного значения длины кривой ![]() по результатам одного и n проездов лаборатории по закруглению. С вероятностью 0,95 такие доверительные интервалы будут
по результатам одного и n проездов лаборатории по закруглению. С вероятностью 0,95 такие доверительные интервалы будут ![]() ,
, ![]() .
.
Отметим, что с вероятностью 0,95 должно выполняться неравенство ![]() , где
, где ![]() и
и ![]() вычисляются соответственно по (3.15) и (3.17). Это может служить контролем правильности наблюдения и вычисления.
вычисляются соответственно по (3.15) и (3.17). Это может служить контролем правильности наблюдения и вычисления.
Исследование устойчивости значений и точности определения длины кривой при различном числе проездов дорожной лаборатории по закруглению «туда-обратно» можно выполнять (как и при исследовании точности измерения угла поворота) путём повторения всех вычислений по ½, 1/3 и ¼ всех значений К. Для этого из n значений К необходимо образовать 2 выборки численностью n/2, 3 выборки численностью n/3 и 4 выборки численностью n/4 и повторить по этим выборкам все вычисления.
Точность измерения радиуса круговой кривой с помощью дорожной лаборатории может быть охарактеризована разностью
![]() , (3.18) где
, (3.18) где ![]() ,
, ![]() - значение радиуса, полученные по данным лаборатории и на основе геодезических измерений.
- значение радиуса, полученные по данным лаборатории и на основе геодезических измерений.
Тогда 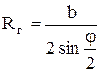 , (3.19) где АВ=ВС= b - измеряются оптическим дальномером.
, (3.19) где АВ=ВС= b - измеряются оптическим дальномером.
Дифференцируя выражение (3.19) по b и ![]() и переходя к средним квадратическим погрешностям, получим
и переходя к средним квадратическим погрешностям, получим 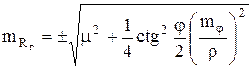 .
.
Относительной погрешностью измерения хорд дальномером 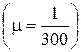 можно пренебречь в связи с её малостью. Так как
можно пренебречь в связи с её малостью. Так как 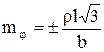 и принимая
и принимая ![]() м; после некоторых преобразования получим
м; после некоторых преобразования получим ![]() .(3.20)
.(3.20)
Одновременно ![]() , (3.21) где
, (3.21) где ![]() ,
, ![]() - средние квадратические погрешности определения радиуса с помощью дорожной лаборатории и геодезическим методом.
- средние квадратические погрешности определения радиуса с помощью дорожной лаборатории и геодезическим методом.
Подставляя в (3.21) значение ![]() на (8.20), будем иметь
на (8.20), будем иметь 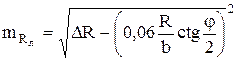 . (3.22)
. (3.22)
Формула (3.22) является окончательной, рабочей. Она позволяет оценивать точность измерения радиуса круговой кривой с помощью дорожной лаборатории.
Важно ещё раз подчеркнуть, что изложенные выше теоретические основы и методика метрологических испытаний лаборатории применимы только на круговой кривой. Теория и методика обследования закругления с целью установления их конструкции и проведения метрологических испытаний лаборатории на закруглениях сложной конструкции требуют особого рассмотрения. Необходимо также исследовать вопрос о зависимости точности оценок геометрических параметров дороги в плане от скорости движения лаборатории. Наконец, самостоятельного рассмотрения и исследования требуют вопросы необходимой точности, которую должна обеспечивать лаборатории при определении различных геометрических параметров дороги в плане, продольном и поперечном профиле.