
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ ОБСЛЕДОВАНИЯ АВТОМОБИЛЬНЫХ ДОРОГ В РАЙОНАХ ЛЕСОЗАГОТОВОК
Лобанов Ю. В., Кондрашова Е. В., Курьянов В. К.,
3.2 Теоретические основы и методика метрологических испытаний лаборатории в продольном профиле дороги
При метрологических испытаниях дорожной лаборатории в продольном профиле необходимо исследовать:
1. Зависит ли точность работы лаборатории от того, работает он на подъёмах или спусках продольного профиля. Для решения этого вопроса обработку результатов на n повторных проездов лаборатории на подъём и на спуск по одному и тому же участку дороги необходимо производить раздельно, с использованием аппарата дисперсионного и корреляционного анализа.
2. Существует ли зависимость между точностью результатов, которые даёт лаборатория, и уклоном продольного профиля дороги. В связи с этим метрологические испытания следует проводить раздельно на участках дорог с малыми (5-15 %), средними (15-30 %) и большими (40-90 %) уклонами. Число таких участков должно быть не менее 8-10, чтобы зависимость ![]() можно было считать достаточно надёжной.
можно было считать достаточно надёжной.
3. Существует ли зависимость между точностью результатов, которые даёт лаборатория, и скоростью её движения. При исследовании этого вопроса результаты, получаемые при различных скоростях движения лаборатории, должны обрабатываться раздельно, с использованием аппарата дисперсионного и регрессионного анализа.
Основные методы исследований: планирование эксперимента при полевых наблюдениях; статистическая обработка данных и проверка статистических гипотез; сравнение результатов, полученных с помощью лаборатории, с аналогичными результатами, полученными на основе геодезических измерений.
Исследование зависимости точности работы лаборатории от знака уклона (на подъёме или спуске) можно совместить с исследованиями второго вопроса - зависит ли точность результатов, которые даёт лаборатория, от величины уклона, продольного профиля. Для этого необходимо выбрать 8-10 участков с различными уклонами 15 ‰![]() i
i ![]() 90 ‰. Участки должны быть пронивелированы методами геометрического или тригонометрического нивелирования между двумя вполне определенными точками, которые необходимо закрепить на кромке покрытия колышками.
90 ‰. Участки должны быть пронивелированы методами геометрического или тригонометрического нивелирования между двумя вполне определенными точками, которые необходимо закрепить на кромке покрытия колышками.
На ![]() проездов лаборатории вверх по данному участку определяем
проездов лаборатории вверх по данному участку определяем ![]() значения уклонов i. Далее вычисляем
значения уклонов i. Далее вычисляем
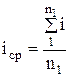 , (3.23)
, (3.23)
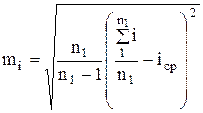 , (3.24)
, (3.24)
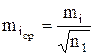 . (3.25)
. (3.25)
Аналогичные вычисления необходимо выполнять по ![]() ,
, ![]() ,
, ![]() значениям уклонов, образовав соответствующие выборки.
значениям уклонов, образовав соответствующие выборки.
Далее с помощью критериев
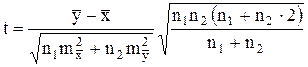 , (3.26)
, (3.26)
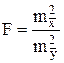 (3.27) необходимо проверить гипотезы о равенстве центров распределения и дисперсий уклонов, полученных по проездам вверх и проездам вниз.
(3.27) необходимо проверить гипотезы о равенстве центров распределения и дисперсий уклонов, полученных по проездам вверх и проездам вниз.
Здесь ![]() ,
, ![]() - средние уклоны, вычисленные раздельно по проездам вверх и проездам вниз;
- средние уклоны, вычисленные раздельно по проездам вверх и проездам вниз; ![]() - число проездов вверх и вниз;
- число проездов вверх и вниз; ![]() - средние квадратические погрешности средних уклонов, вычисленные по результатам проездов вверх и вниз.
- средние квадратические погрешности средних уклонов, вычисленные по результатам проездов вверх и вниз.
Проверку гипотез необходимо повторить по выборкам ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Далее необходимо вычислить разности
. Далее необходимо вычислить разности ![]() , где
, где ![]() - уклоны, полученные с помощью лаборатории и геодезическим методом. Разности должны быть вычислены раздельно по результатам проездов вверх и вниз и по всем выборочным значениям
- уклоны, полученные с помощью лаборатории и геодезическим методом. Разности должны быть вычислены раздельно по результатам проездов вверх и вниз и по всем выборочным значениям ![]() /
/
Затем с помощью критериев (3.26), (3.27) следует проверить гипотезы о равенстве центров распределения и дисперсий величин ![]() и
и ![]() - разности, вычисленные соответственно по результатам проездов вверх и вниз. В случае зависимости величин разностей от направления проездов лаборатории необходимо продолжить их статистическую обработку, чтобы получить величину или зависимость для вычисления систематической погрешности и затем поправки.
- разности, вычисленные соответственно по результатам проездов вверх и вниз. В случае зависимости величин разностей от направления проездов лаборатории необходимо продолжить их статистическую обработку, чтобы получить величину или зависимость для вычисления систематической погрешности и затем поправки.
Зависимость разностей ![]() от числа проездов целесообразно изобразить графически и аппроксимировать уравнением. Для этого на графике, кроме единичных значений
от числа проездов целесообразно изобразить графически и аппроксимировать уравнением. Для этого на графике, кроме единичных значений ![]() следует показать усредненные значения из
следует показать усредненные значения из ![]() ,
, ![]() и
и ![]() значений
значений ![]() . Можно вычислить также средние квадратические отклонения величин
. Можно вычислить также средние квадратические отклонения величин ![]() и построить доверительные интервалы для
и построить доверительные интервалы для ![]() . Зависимость разностей от числа проездов можно использовать для определения оптимального числа проездов.
. Зависимость разностей от числа проездов можно использовать для определения оптимального числа проездов.
Для установления зависимости точности работы дорожной лаборатории от уклона продольного профиля аналогичные статистические исследования необходимо повторить на участках с различными значениями уклона. При этом раздельно должны обрабатываться и сравниваться результаты проездов вниз по нескольким участкам и результаты проездов вверх по тем же участкам.
Порядок обработки данных может быть следующий. Вычисляют по участку 1 (по проездам вверх) статистики: (3.23), (3.24), (3.25) по n проездам. Аналогичные статистики вычисляют по участкам 2,3...,k (k ![]() 8-10). Строят графики функции
8-10). Строят графики функции ![]() и
и ![]() по эмпирическим значениям (точкам)
по эмпирическим значениям (точкам)![]() .
. ![]() и i. Проверяют гипотезу о равенстве дисперсий попарно на нескольких участках (например 1 и 2; 1 и 3; 1 и 4; 2 и 3; 2 и 4; и т.д.).
и i. Проверяют гипотезу о равенстве дисперсий попарно на нескольких участках (например 1 и 2; 1 и 3; 1 и 4; 2 и 3; 2 и 4; и т.д.).
Если эмпирические графики и процедуры проверки равенства дисперсий обнаруживают зависимость погрешностей ![]() и
и ![]() от значений уклонов, то необходимо вычислить соответствующие коэффициенты корреляции, корреляционные отношения, проверить их статистическую значимость и вычислить аппроксимирующее уравнение. Аналогичную проверку следует повторить по результатам проездов вниз. Желательно также и те другие вычисления повторить по выборкам численностью
от значений уклонов, то необходимо вычислить соответствующие коэффициенты корреляции, корреляционные отношения, проверить их статистическую значимость и вычислить аппроксимирующее уравнение. Аналогичную проверку следует повторить по результатам проездов вниз. Желательно также и те другие вычисления повторить по выборкам численностью ![]() ,
, ![]() и
и ![]() .
.
Проверку зависимости точности работы лаборатории от скорости её движения можно произвести по аналогичной методике, используя данные проездов лаборатории вверх-вниз с различными скоростями по нескольким участкам с разными уклонами. В этом случае анализу и сравнению должны быть подвергнуты идентичные статистики, полученные при разных скоростях проезда на одном и том же участке. Затем можно сравнить между собой эти же статистики, полученные на разных участках с разными уклонами.