Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Частично пористые газостатические опоры шпиндельных узлов. Теория и эксперимент: монография

Космынин А. В., Виноградова С. В., Виноградов В. С., Щетинин В. С., Смирнов А. В.,

3.3. Оценка погрешности определения экспериментальных данных

Экспериментальные значения эксплуатационных характеристик подшипников определяются косвенным путем с помощью различных измерительных инструментов и приборов, которые имеют определенную степень точности. Поэтому для корректного анализа опытных данных необходимо найти суммарное влияние этих погрешностей на результаты экспериментов.

Как уже отмечалось, с целью определения коэффициента жесткости смазочного слоя экспериментальные зависимости радиальных подшипников с частично пористой стенкой вкладыша  методом наименьших квадратичных отклонений аппроксимировались полиномом, который имеет вид:

,           (3.2)

где  - сглаженное значение коэффициента несущей способности.

Тогда на основании уравнений (3.1) и (3.2) получается следующее выражение для расчета коэффициента жесткости смазочного слоя:

,

где  - сглаженное значение коэффициента жесткости смазочного слоя.

Необходимость аппроксимации зависимостей C_Q для нахождения значений k_S требует иного подхода в определении погрешности эксперимента, как это изложено, например, в работе [148]. Такой метод анализа погрешностей корректно может быть выполнен на основе математической теории корреляции [154], который и используется в настоящей работе.

Согласно этой теории значение доверительного интервала некоторой случайной величины  с доверительной вероятностью  определяется по формуле:

,

где  - сглаженное значение случайной величины ;  -  q %-й предел для распределения Стьюдента; N - число наблюдений; n - число неизвестных коэффициентов полинома;  - оценка дисперсии случайной величины .

Оценка дисперсии рассчитывается по формуле:

,

где  - транспонированный вектор-столбец известных параметров полинома;  - матрица размером  значений вектора  при различных наблюдениях (  - значение j-й составляющей вектора  при i-м наблюдении);  - оценка дисперсии случайной помехи η.

Оценка дисперсии  равна:

,

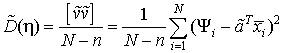где 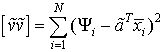 - сумма квадратов невязок, т.е. разностей между экспериментальными и сглаженными результатами.

Так, например, при расчете дисперсии  случайной величины  вектор , а матрица B имеет вид:

.

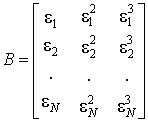Для коэффициента жесткости  вектор  и, следовательно, матрица B имеет следующий вид:

.

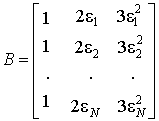Помеха η для  имеет то же значение, что и для , так как параметр  при помощи соответствующего оператора получается на основе наблюденных значений . Следовательно, величина дисперсия случайной помехи  для коэффициентов  и  будет одинаковой.

Найденные на основе представленных формул доверительные интервалы коэффициентов несущей способности и жёсткости смазочного слоя при доверительной вероятности 0,95 позволили найти максимальные относительные погрешности этих величин. Как показали расчеты, максимальные погрешности коэффициентов  и  достигаются при больших осевых зазорах и относительных эксцентриситетах. Обработка результатов выполненных экспериментов показала, что максимальные погрешности определения эксплуатационных характеристик исследуемого подшипника равны:  4,5 %;  5,1 %.