Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Частично пористые газостатические опоры шпиндельных узлов. Теория и эксперимент: монография
Космынин А. В., Виноградова С. В., Виноградов В. С., Щетинин В. С., Смирнов А. В.,
2.2.1. Определение поля давления в зазоре подшипника
Дифференциальное уравнение (2.13) представляет собой уравнение эллиптического типа в частных производных, аналитическое решение которого остается нерешенной задачей. Поэтому решим уравнение Рейнольдса численным интегрированием [150].Запишем выражение (2.13) в конечно-разностной форме. Для этого сначала его приведем к виду:
,
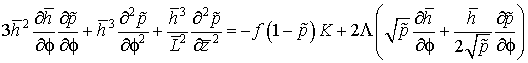где 
.
Введем обозначение
,
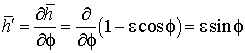и с учетом этого получим:
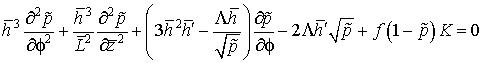. (2.14)
Выражение (2.14) является исходным для определения поля давления в зазоре подшипника путем численного интегрирования.
Разобьем область интегрирования 
на 
узлов, где 
- количество горизонтальных линий сетки, 
- количество вертикальных линий сетки. Шаг изменения переменных 
и 
, следовательно, будет равен (рис. 2.4):
.
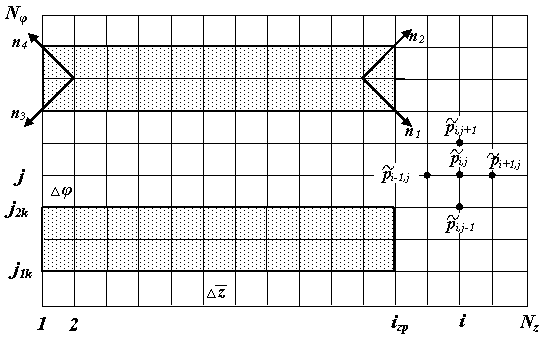
Рис. 2.4. Шаблон конечно-разностной сетки области интегрирования
Текущие координаты узлов сетки находятся из уравнений:
, i=1, 2, 3,... , 
, j=1, 2, 3, ... .
Обозначим координаты точек конечно-разностной сетки через координаты узлов (i, j) и заменим все частные производные, которые содержит уравнение (2.14) центральными конечными разностями по формулам:
;
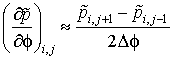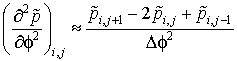; (2.15)
.
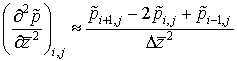С учетом уравнений (2.15) выражение (2.14) в конечно-разностной форме примет вид:
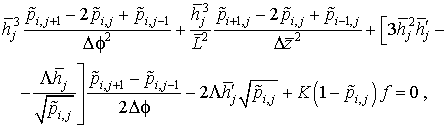
где 
, j=1, 2, 3, ... .
Из последнего уравнения выразим величину 
:
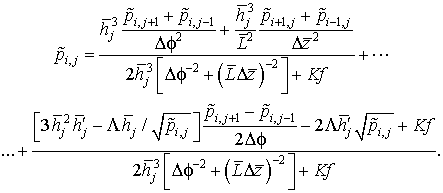(2.16)
В соответствие с представленной на рис. 2.4 областью интегрирования поставим граничные условия решаемой задачи с учетом дискретного расположения пористых ограничителей расхода. Попутно заметим, что с целью упрощения расчетов шпоночная форма вставок заменена эквивалентной ей по площади прямоугольной формой.
Граничные условия на внешнем контуре конечно-разностной сетки имеют вид:
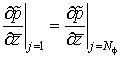; (2.17)
; (2.18)
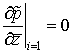; (2.19)
. (2.20)
Граничное условие на вертикальных линиях контура пористых вставок при 
и 
, где k = 1, 2, ... следующее:
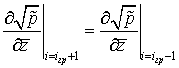. (2.21)
Граничные условия на горизонтальных линиях контура пористых вставок при 
:
- нижняя граница k-той вставки (
)
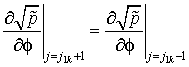; (2.22)
- верхняя граница k-той вставки (
):
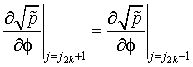. (2.23)
Граничные условия в точках пересечения вертикальных и горизонтальных линий контура пористых вставок:
- в точках с координатами 
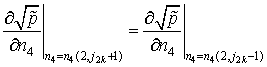; (2.24)
- в точках с координатами 
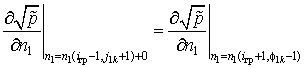; (2.25)
- в точках с координатами 
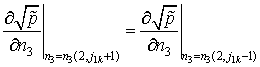; (2.26)
- в точках с координатами 
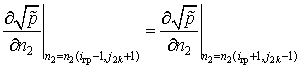. (2.27)
Совокупная система уравнений (2.16)-(2.27) является замкнутой, так как позволяет определить давление газа в любом узле конечно-разностной сетки.
Кроме границ пористых вставок относительное давление 
определяется согласно (2.16) во внутренних узлах области интегрирования и с учетом (2.17)-(2.20) на ее границе. Исходя граничных условий, запишем систему алгебраических разностных уравнений, с помощью которых находится относительное давление на границах разностной сетки и пористых вставок. При этом будем иметь в виду четность функции :
.
Принимая во внимание граничные условия (2.17) и (2.18), выражения для определения давления в точках, лежащих на линиях j=1 и , 
имеют вид:
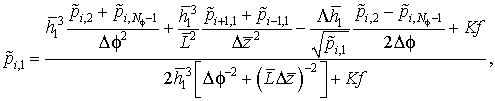
где i = 2, 3, ... 
.
С учетом граничного условия (2.19) уравнение для давления в точках, расположенных на линии i = 1, имеет следующую форму записи:
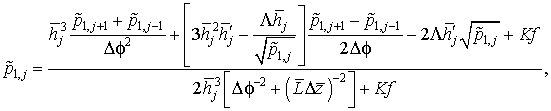
где j = 2, 3, ... 
.
Давление газа в точках с координатами (1, 1) и (1, ) находится из выражения:
.
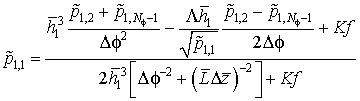Формула для расчета давления во внутренних точках вертикальных границ k-той пористой вставки при 
имеет вид:
, 
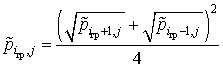. (2.28)
Во внутренних точках горизонтальных границ пористых вставок давление находится из выражений:
- на линиях k-й вставки
, 
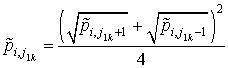; (2.29)
- на линиях k-й вставки
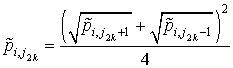, . (2.30)
Формулы для расчета давления в точках пересечения вертикальных и горизонтальных граничных линий пористых вставок имеют следующий вид:
- в точках с координатами (
)
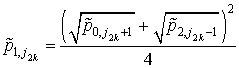; (2.31)
- в точках с координатами (
)
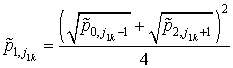; (2.32)
- в точках с координатами (
)
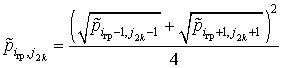; (2.33)
- в точках с координатами (
)
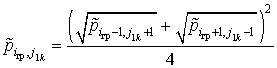. (2.34)