Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Горева Т. С., Портнягин Н. Н.,
1.1. Многомерное преобразование Фурье
Преобразование Фурье - операция, сопоставляющая функциивещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие -гармонические колебания с разными частотами.Преобразование Фурье функции f вещественной переменной является интегральным преобразованием и задается следующей формулой:
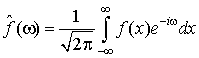. (1.1)
Преобразование Фурье является линейным оператором: Справедливо равенство Парсеваля: если 
, то преобразование Фурье сохраняет L2-норму:
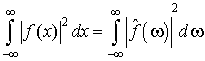. (1.2)
Это свойство позволяет по непрерывности распространить определение преобразования Фурье на всё пространство 
. Равенство Парсеваля будет при этом справедливо для всех 
.
Формула обращения: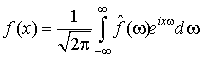 
справедлива, если интеграл в правой части имеет смысл. В частности, это верно, если функция f является достаточно гладкой. Если , то формула также верна, поскольку равенство Парсеваля позволяет придать интегралу в правой части смысл с помощью предельного перехода.
Теорема о свертке: если 
, тогда , тогда 
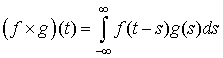
. (1.3)
Преобразование Фурье используется во многих областях науки - в физике, теории чисел, комбинаторике, обработке сигналов, теории вероятностей, статистике, криптографии, акустике, океанологии, оптике, геометрии, и многих других. В обработке сигналов и связанных областях преобразование Фурье обычно рассматривается как декомпозиция сигнала на частоты и амплитуды, то есть, обратимый переход от временного пространства (time domain) в частотное пространство (frequency domain). Богатые возможности применения основываются на нескольких полезных свойствах преобразования:
- Преобразования являются линейными операторами и, с соответствующей нормализацией, также являются унитарными (свойство, известное как теорема Парсеваля или, в более общем случае как теорема Планшереля, или в наиболее общем как дуализм Понтрягина).
- Преобразования обратимы, причём обратное преобразование имеет практически такую же форму, как и прямое преобразование.
- Синусоидальные базисные функции (вернее, комплексные экспоненты) являются собственными функциямидифференцирования, что означает, что данное представление превращает линейные дифференциальные уравнения с постоянными коэффициентами в обычные алгебраические. (Например, в линейной стационарной системе частота-консервативная величина, поэтому поведение на каждой частоте может решаться независимо.)
- По теореме о свёртке, преобразование Фурье превращает сложную операцию свёртки в простое умножение, что означает, что они обеспечивают эффективный способ вычисления основанных на свёртке операций, таких как умножение многочленов и умножение больших чисел.
- Дискретная версия преобразования Фурье может быстро рассчитываться на компьютерах, используя алгоритм быстрого преобразования Фурье (БПФ, англ.FFT).
Преобразование Фурье функций, заданных на пространстве 
, определяется формулой:
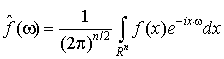; (1.5)
здесь ω и x - векторы пространства 
- их скалярное произведение.
Обратное преобразование в этом случае задается формулой
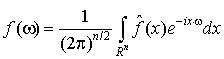. (1.6)
Эта формула может быть интерпретирована как разложение функции f в линейную комбинацию (суперпозицию) «плоских волн» вида 
с амплитудами, частотами ω и фазовыми сдвигами 
соответственно.
В терминах обработки сигналов, преобразование берёт представление функции сигнала в виде временных рядов и отображает его в частотный спектр, где ω -угловая частота. То есть оно превращает функцию времени в функцию частоты; это разложение функции на гармонические составляющие на различных частотах.
Когда функция f является функцией времени и представляет физический сигнал, преобразование имеет стандартную интерпретацию как спектр сигнала. Абсолютная величина получающейся в результате комплексной функции F представляет амплитуды соответствующих частот (ω), в то время как фазовые сдвиги получаются как аргумент этой комплексной функции.
Однако важно осознавать, что преобразования Фурье не ограничиваются функциями времени и временными частотами. Они могут в равной степени применяться для анализа пространственных частот, также как для практически любых других функций.