
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.2. Дискретное преобразование Фурье
Дискретное преобразование Фурье - преобразование конечных последовательностей (комплексных) чисел, которое, как и в непрерывном случае, превращает свёртку в поточечное умножение. Используется в цифровой обработке сигналов и в других ситуациях, где необходимо быстро выполнять свёртку, например, при умножении больших чисел.Любой сигнал с периодом N может быть представлен в виде суммы дискретных синусоидальных волн. Пространство сигналов с периодом N - это евклидово пространство размерности N, и скалярное произведение двух таких сигналов f и g:
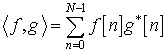 . (1.7)
. (1.7)
Ортогональный базис пространства сигналов с периодом N представляем в виде:
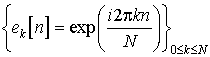 . (1.8)
. (1.8)
Так как пространство имеет размерность N, то любое ортогональное семейство из N векторов образует ортогональный базис. Любой сигнал f с периодом Nможет быть разложен по этому базису:
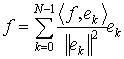 . (1.9)
. (1.9)
Дискретное преобразование Фурье (ДПФ) есть:
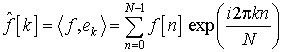 . (1.10)
. (1.10)
Так как ![]() , получим формулу обратного дискретного преобразования Фурье:
, получим формулу обратного дискретного преобразования Фурье:
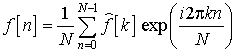 . (1.11)
. (1.11)
Важно рассматривать периодический сигнал с периодом N вместо конечного сигнала по N отсчетам. Если ![]() и
и ![]() сильно отличаются друг от друга, то это приведет к резкому скачку в периодическом сигнале в результате - относительно большим амплитудам коэффициентов Фурье для высоких частот. [4,5]
сильно отличаются друг от друга, то это приведет к резкому скачку в периодическом сигнале в результате - относительно большим амплитудам коэффициентов Фурье для высоких частот. [4,5]
