Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Методы построения активных фильтров подавления импульсных помех в сетях электропитания промысловых судов

Горева Т. С., Портнягин Н. Н.,

1.3. Преобразование Фурье с окном

Преобразование Фурье является эффективным средством исследовании сигналов. Однако оно имеет недостаток, который заключается в слабой пространственной локализации. Это проявляется, во-первых, в том, что длянахождении преобразовании Фурье  необходимо знать сигнал  полностью на всей числовой прямой R.

Во-вторых, положение и величина «пиков» функции  не получается легко из , поскольку данное значение  формируется с учетом всех значений функции . Улучшить пространственную локализацию можно за счет искусственной локализации сигнала. Для этого можно умножить сигнал  на подходящую функцию , которая имеет носитель вблизи точки x₀. В результате получаем оконное преобразование Фурье:

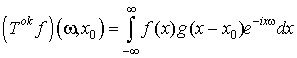.               (1.12)

Размер носителя функции  определяет ширину окна. [14]

Оконное преобразование Фурье

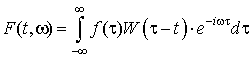,                   (1.13)

где  даёт (вообще говоря, несколько искажённое) распределение частот части оригинального сигнала f(t) в окрестности времени t. Классическое преобразование Фурье имеет дело со спектром сигнала, взятым во всем диапазоне существования переменной. Нередко интерес представляет только локальное распределение частот, в то время как требуется сохранить изначальную переменную (обычно время). В этом случае используется обобщение преобразования Фурье, так называемое оконное преобразование Фурье. Для начала необходимо выбрать некоторую оконную функцию W, эта функция должна иметь хорошо локализованный спектр. На практике дискретный спектральный анализ реализован в современных цифровых осциллографах и анализаторах спектра. Используется, как правило, выбор окна из 3-10 типов окон. Применение окон принципиально необходимо, поскольку в реальных приборах исследуется всегда некоторая вырезка из исследуемого сигнала. При этом разрывы сигнала вследствие вырезки резко искажают спектр из-за наложения спектров скачков на спектр сигнала. Некоторые анализаторы спектра используют быстрое (или кратковременное) оконное преобразование. При нём сигнал заданной длительности разбивается на ряд интервалов с помощью скользящего окна того или иного типа. Это позволяет получать, исследовать и строить в виде спектрограмм динамические спектры и анализировать их поведение во времени. Спектрограмма строится в трёх координатах - частота, время и амплитуда. При этом амплитуда задаётся цветом или оттенком цвета каждого прямоугольника спектрограммы. Подобные анализаторы спектра называют анализаторами спектра реального времени. Основным их производителем является корпорация Tetronix (США). Такие анализаторы появились в конце прошлого века и ныне бурно развиваются. Частотный диапазон исследуемых ими сигналов достигает сотен ГГц. Указанные методы спектрального анализа реализуются и в системах компьютерной математики, например, Mathcad, Mathematica, Maple и MATLAB.

Дискретное преобразование Фурье является частным случаем (и иногда применяется для аппроксимации) дискретного во времени преобразования Фурье (DTFT), в котором x_k определены на дискретных, но бесконечных областях, и таким образом спектр является непрерывным и периодическим. Дискретное во времени преобразование Фурье является по существу обратным для рядов Фурье.

Эти разновидности преобразования Фурье могут быть обобщены на преобразования Фурье произвольных локально компактных абелевых топологических групп, которые изучаются в гармоническом анализе; они преобразуют группу в её дуальную группу. Эта трактовка также позволяет сформулировать теорему свёртки, которая устанавливает связь между преобразованиями Фурье и свёртками.