
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.4. Частотно-временная локализация
Свойство частотной и временной локализации вейвлет-функцийможет быть охарактеризовано концентрацией их энергии в частотной и временной областях, или посредством частотно-временных окон.
Построение частотно-временных окон основывается на определении вторых центральных моментов (дисперсии) функций ![]() и
и ![]() , квадратный корень из которых как раз характеризует область наибольшей концентрации энергии.
, квадратный корень из которых как раз характеризует область наибольшей концентрации энергии.
Рассчитаем первый начальный (математическое ожидание) и второй центральный моменты функции ![]() следующим образом:
следующим образом:
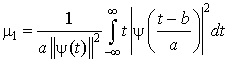 , (2.27)
, (2.27)
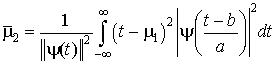 , (2.28)
, (2.28)
где 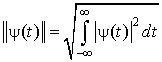 - норма базисной вейвлет-функции.
- норма базисной вейвлет-функции.
Тогда после замены переменной ![]() и преобразований, связанных с ее введением под знак интеграла (1.27), получим:
и преобразований, связанных с ее введением под знак интеграла (1.27), получим:
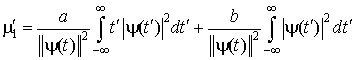 .
.
Поскольку норма и энергия вейвлет-функции взаимосвязаны соотношением таким, что 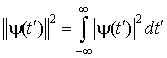 , в то время как
, в то время как 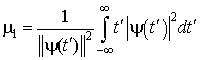 представляет собой первый начальный момент функции
представляет собой первый начальный момент функции ![]() (1.27), оказывается очевидным тот факт, что результирующее выражение для
(1.27), оказывается очевидным тот факт, что результирующее выражение для ![]() принимает вид:
принимает вид:
![]() (2.29)
(2.29)
Другими словами, всякая дилатация, осуществляемая над материнской вейвлет-функцией, приводит к пропорциональному увеличению расстояния между центрами тяжести ее клонов.
Подставим выражение (1.29) в выражение для второго центрального момента вейвлет-функции, в результате чего получим:
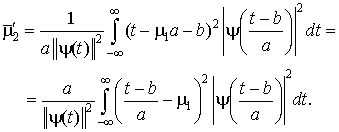 .
.
Введя в данном выражении обозначение ![]() , перепишем его в следующем виде:
, перепишем его в следующем виде:
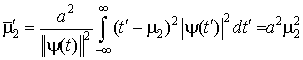 (2.30)
(2.30)
Выражение (1.30) определяет величину, представляющую собой квадрат диаметра вейвлет-функции, рассматриваемой во временной области.
Сказанное означает, что вейвлет-функция занимает временное окно
![]() , (2.31)
, (2.31)
а также обладает носителем ![]() с центром в точке
с центром в точке ![]() .
.
Можно сказать, что сингулярность сигнала ![]() , рассматриваемая в точке , может быть аппроксимирована с меньшей погрешностью при задании меньших значений масштабирующей переменной вейвлета, т.е. при попадании на плоскости
, рассматриваемая в точке , может быть аппроксимирована с меньшей погрешностью при задании меньших значений масштабирующей переменной вейвлета, т.е. при попадании на плоскости ![]() в так называемый угол влияния. В то же время, значение функции
в так называемый угол влияния. В то же время, значение функции ![]() в точке
в точке ![]() может быть определено по значению сигнала f(t), взятому в точке b0 при условии попадания в такой же угол. Мелкомасштабные сингулярности сигнала получают наилучшее отображение на плоскости (a,b) в случае задания малых значений переменной a вейвлет-функции, одновременно с этим претерпевая сглаживание при больших ее значениях, которые, в свою очередь, способствуют проявлению, как раз напротив, ламинарностей сигнала.
может быть определено по значению сигнала f(t), взятому в точке b0 при условии попадания в такой же угол. Мелкомасштабные сингулярности сигнала получают наилучшее отображение на плоскости (a,b) в случае задания малых значений переменной a вейвлет-функции, одновременно с этим претерпевая сглаживание при больших ее значениях, которые, в свою очередь, способствуют проявлению, как раз напротив, ламинарностей сигнала.
Определим аналогичным образом локальные свойства вейвлет-функции в частотной области, полагая, что ![]() представляет собой второй центральный момент образа Фурье
представляет собой второй центральный момент образа Фурье 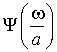 функции.
функции.
С целью записи континуального вейвлет-преобразования в частотной области воспользуемся нотацией Фурье, а также равенством Парсеваля:
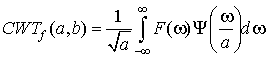 ,
,
т.е. констатируем тот факт, что вейвлет-преобразование представляет собой полосовой фильтр с настройкой ω0 и шириной полосы пропускания ![]() . Действительно, процедура дилатации, осуществляемая над вейвлет-функцией во временной области, соответствует обратному изменению ширины полосы пропускания фильтра в спектральной области: например, при уменьшении ширины носителя вейвлет-функции полоса пропускания фильтра увеличивается и наоборот.
. Действительно, процедура дилатации, осуществляемая над вейвлет-функцией во временной области, соответствует обратному изменению ширины полосы пропускания фильтра в спектральной области: например, при уменьшении ширины носителя вейвлет-функции полоса пропускания фильтра увеличивается и наоборот.
Таким образом, можно сделать вывод о том, что вейвлет-преобразование обеспечивает информацией о спектре сигнала в полосе частот ![]() , т.е. в окне
, т.е. в окне 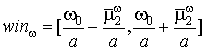 , имеющем носитель
, имеющем носитель 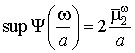 .
.
Свойство вейвлет-функций осуществлять спектральный анализ сигналов с постоянной добротностью, можно подтвердить также тем фактом, что площадь частотно-временного окна, занимаемого вейвлет-функцией, также остается неизменной для любых значений масштабирующей переменной и равной 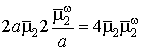 (рис. 2.2). Данное свойство удовлетворяет принципу неопределенности Гейзенберга, утверждающему, что увеличение носителя вейвлет-функции во временной области приводит к уменьшению ее спектральной полосы и, наоборот, временное сжатие функции соответствует увеличению носителя ее образа Фурье.
(рис. 2.2). Данное свойство удовлетворяет принципу неопределенности Гейзенберга, утверждающему, что увеличение носителя вейвлет-функции во временной области приводит к уменьшению ее спектральной полосы и, наоборот, временное сжатие функции соответствует увеличению носителя ее образа Фурье.
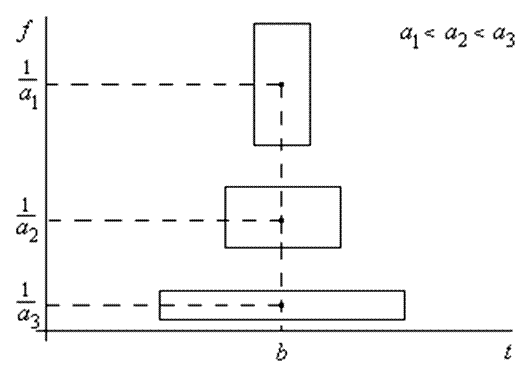
Рис.2.2. Частотно-временное окно вейвлет-функции
