
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.2.1. Ортогональные вейвлеты
Ортонормированные вейвлеты являются носителями подробностей, необходимых для повышения разрешения аппроксимации сигнала. Аппроксимации fс масштабами Vj и Vj-1. Vj содержится вVj-1. Пусть Wj -ортогональное дополнение Vj в Vj-1:
![]() . (2.18)
. (2.18)
Ортогональная проекция f на Vj-1 может быть предназначена как сумма ортогональных проекций на Vj и Wj:
![]() (2.19)
(2.19)
Дополнение ![]() несет в себе «детали» f, которые появляются при масштабе 2j-1, но которые пропадают при более грубом масштабе 2j. В следующей теореме доказывается, что можно построить ортонормированный базис в Wj, масштабируя и сдвигая вейвлет
несет в себе «детали» f, которые появляются при масштабе 2j-1, но которые пропадают при более грубом масштабе 2j. В следующей теореме доказывается, что можно построить ортонормированный базис в Wj, масштабируя и сдвигая вейвлет ![]() .
.
Пусть φ - масштабирующая функция и h - соответствующий сопряженный зеркальный фильтр. Пусть ψ - функция, преобразования Фурье которой есть
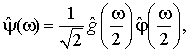 (2.20)
(2.20)
где
![]() (2.21)
(2.21)
Обозначим
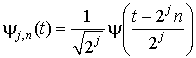 .
.
![]() - ортонормированный базис Wj для любого масштаба 2j. При всех масштабах
- ортонормированный базис Wj для любого масштаба 2j. При всех масштабах ![]() есть ортонормированный базис
есть ортонормированный базис ![]()
Семейство ![]() - ортогональный базис Wj тогда и только тогда, когда
- ортогональный базис Wj тогда и только тогда, когда
![]() ; (1.22)
; (1.22)
![]() . (2.23)
. (2.23)
