
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.2.2. Нулевые моменты вейвлетов
В применениях вейвлет-базисов используется их способность эффективно аппроксимировать специальные классы функций с помощью небольшого числа нулевых вейвлет-коэффициентов. Это верно при удалении шума и быстрых вычислениях. Поэтому построение ψ должно быть оптимизировано в смысле получения максимального числа вейвлет-коэффициентовВейвлет ψ имеет p нулевых моментов, если
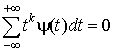 для
для ![]() . (2.24)
. (2.24)
Это означает, что ортогонален любому многочлену степени p - 1. Если f - гладкая функция и имеет достаточно нулевых моментов, то вейвлет-коэффициенты ![]() малы при малых масштабах 2j.
малы при малых масштабах 2j.
Пусть ψ и φ - вейвлет и масштабирующая функция, которые порождают ортогональные базисы. Предположим, что ![]() и
и ![]() . Четыре следующих утверждения эквивалентны:
. Четыре следующих утверждения эквивалентны:
(1) Вейвлет ψ имеет p нулевых моментов.
(2) ![]() и его первые p - 1 производная равны нулю при ω=0.
и его первые p - 1 производная равны нулю при ω=0.
(3) ![]() и его первые p - 1 производная равны нулю при
и его первые p - 1 производная равны нулю при ![]() .
.
(4) При любом ![]()
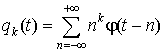 - многочлен степени k.
- многочлен степени k.
Утверждение (4) называется условием Фикса-Стрэнга. Полиномы ![]() определяют базис пространства многочленов степени p - 1. Поэтому условие Фикса-Стрэнга утверждает, что имеет p нулевых моментов тогда и только тогда, когда любой многочлен степени p-1 может быть представлен как линейная комбинация
определяют базис пространства многочленов степени p - 1. Поэтому условие Фикса-Стрэнга утверждает, что имеет p нулевых моментов тогда и только тогда, когда любой многочлен степени p-1 может быть представлен как линейная комбинация ![]() . Коэффициенты разложения многочленов qk не имеют конечной энергии, потому что её не имеют сами многочлены.
. Коэффициенты разложения многочленов qk не имеют конечной энергии, потому что её не имеют сами многочлены.
