Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.5.Вероятность образования сложных структур и энтропия
Для количественного анализа процессов введем математическое выражение для энтропии, которую будем рассматривать как величину пропорциональную статистическому весу системы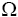 
. Коэффициентом пропорциональности служит постоянная Больцмана k:
S= k×ln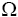. (2)
В свою очередь, статистический вес с заданным числом частиц в каждой ячейке N1, N2, … Nm определяется как отношение:
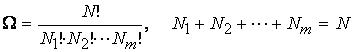(3)
где N – полное число частиц. [89, 197].
Рассмотрим систему, в которой элементы не могут образовывать связи между собой. Посчитаем вероятность и статистический вес системы при различном распределении частиц по двум одинаковым объемам. Для двух частиц возможны всего 4 распределения (таблица 2).
Таблица 2.
| Возможные распределения | 2 и 0 | 1 и 1 |
| Число возможностей | 2 | 2 |
| Вероятность | 1/2 | 1/2 |
| Статистический вес | 1 | 2 |
Для трех частиц при 8 возможных распределениях получим следующие данные (таблица 3).
Таблица 3.
| Возможные распределения | 3 и 0 | 2 и 1 |
| Число возможностей | 2 | 6 |
| Вероятность | 1/4 | 3/4 |
| Статистический вес | 1 | 3 |
В таблицах 4-6 представлены аналогичные данные для 4, 5 и 6 частиц.
Таблица 4.
| Возможные распределения | 4 и 0 | 3 и 1 | 2 и 2 |
| Число возможностей | 2 | 8 | 6 |
| Вероятность | 1/8 | 4/8 | 3/8 |
| Статистический вес | 1 | 4 | 6 |
Таблица 5.
| Возможные распределения | 5 и 0 | 4 и 1 | 3 и 2 |
| Число возможностей | 2 | 10 | 20 |
| Вероятность | 1/16 | 5/16 | 10/16 |
| Статистический вес | 1 | 5 | 10 |
Таблица 6.
| Возможные распределения | 6 и 0 | 5 и 1 | 4 и 2 | 3 и 3 |
| Число возможностей | 2 | 12 | 30 | 20 |
| Вероятность | 1/32 | 6/32 | 15/32 | 10/32 |
| Статистический вес | 1 | 6 | 15 | 20 |
Как видим, наиболее вероятное состояние системы соответствует распределению частиц, которое близко к равномерному. Этому же состоянию соответствует максимальный статистический вес, что тождественно максимуму энтропии. Изменение статистического веса при неизменном числе частиц происходит за счет их перераспределения между частями сосуда. При этом в формуле (3) изменяется знаменатель.
Теперь рассмотрим систему, в которой возможно образование связей между составляющими ее элементами.
Пусть имеется шесть частиц, которые могут определенными образом распределяться по двум объемам. Максимально возможный статистический вес при этом равен 20 (таблица 6). Если же две частицы объединяются в единое целое, в системе будет уже 5 частиц, а максимально возможный статвес – 10 (таблица 5). При дальнейшем объединении при 4 частицах максимальный статвес равен 6 (таблица 4), при 3 частицах – 3 (таблица 3). При этом в формуле (3) меняется числитель, то есть идет качественно иной физический процесс.
Таким образом, при образовании связи между частицами статистический вес системы, а следовательно, и энтропия, уменьшаются. Причем, это обусловлено свойствами самой системы, точнее составляющих ее элементов.
Возможна и другая интерпретация вышеуказанных формул: при образовании связей в число микросостояний системы надо включить число возможных взаимодействий между отдельными элементами системы. Тогда число N будет возрастать и при образовании структуры энтропия – увеличиваться. Тогда в соответствии с подходом С.Д. Хайтуна энтропия не может являться мерой беспорядка.
Таким образом, образование связей осуществляется на основе какого-то фундаментального взаимодействия посредством поля. По сути дела мы имеем следующее: наличие поля, которое выступает посредником при образовании связей между элементами, делает возможным образование структур. Такое решение проблемы рассматривалось ранее в одном из подходов, о чем было сказано выше.
Однако, в этом случае считается, что вероятность образования связей достаточно мала, и идет не нарушение второго закона термодинамики, а просто в силу случайности происходит событие с малой вероятностью. При таком подходе образование структур выступает все-таки как маловероятное, а не закономерное событие. Однако, такой подход не является корректным
Предположим, что вероятность образования связи между двумя элементами системы при однократном взаимодействии равна 0,1. Тогда вероятность не образования связи равна 0,9. После второй попытки вероятность не образования связи равна 0,92=0,81, вероятность же того, что связь образуется, равна 1-0,81 =0,19.
Данные для вероятности не образования и образования связей при различном числе попыток представлены в таблице 7.
Таблица 7
| Число попыток | Вероятность не образования связи | Вероятность образования связи |
| 1 | 0,9 | 0,1 |
| 2 | 0,81 | 0,19 |
| 3 | 0,729 | 0,271 |
| 4 | 0,656 | 0,344 |
| 5 | 0,590 | 0,410 |
| ------------------ | -------------------------------- | -------------------------------------- |
| 100 | 2,66·10-5 | ≈1 |
В общем виде это можно выразить следующим образом.
Пусть вероятность образования связи между двумя элементами при их взаимодействии 0<p<1.
Тогда вероятность того, при взаимодействии структура не образуется равна 1– р. При числе взаимодействий, равным n, вероятность не образования связи будет равна (1– р)n. При стремлении числа взаимодействий к бесконечности вероятность того, что связь не сможет образоваться, можно найти как предел:
(4)
поскольку 0<k<1. Вероятность же образования связи при n→∞ будет равна 1.
Таким образом, при любой, неравной нулю, вероятности образования какой-либо связи она неизбежно образуется, и это как раз будет наиболее вероятное состояние системы.
Итак, в нашей методологической концепции выявлена конкретная причина образования таких связей – стремление системы к наиболее вероятному состоянию.
Таким образом, можно сделать вывод: предоставленная самой себе система стремится к наиболее вероятному состоянию. Если между элементами системы невозможно образование связей, то наиболее вероятное состояние соответствует термодинамическому равновесию; если же образование связей возможно, то наиболее вероятное состояние соответствует образованию структуры.