Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ПЛАЗМЕННО-ГИДРОДИНАМИЧЕСКАЯ КОНЦЕПЦИЯ СОСТОЯНИЯ ИОНОВ В РАСТВОРАХ ЭЛЕКТРОЛИТОВ В ОЦЕНКЕ НЕКОТОРЫХ СВОЙСТВ

Балданова Д М, Танганов Б Б,

1.2.1. Электропроводность

Электропроводность относится к кинетическим явлениям или явлениям переноса. Одним из теоретических методов исследования явления переноса является кинетический метод Больцмана, раскрывающий зависимость удельной электропроводности  и подвижности носителей тока u от усредненного по энергиям эффективного времени релаксации τ [13]:

,

где  – подвижность носителей тока; n – плотность числа частиц.

Начало исследованиям растворов электролитов характеризуется использованием эмпирических зависимостей электропроводности от концентрации. Первое выражение было предложено Кольраушем [14], который экспериментально установил, что в ряде случаев в разбавленных растворах изменение эквивалентной электропроводности  линейно зависит от квадрата корня концентрации  электролита:

.

Для некоторых разбавленных электролитов лучшее совпадение экспериментальными данными получается, если используется кубический корень из концентраций:

.

Эквивалентная электропроводность раствора электролита при бесконечном разбавлении  равна сумме предельных подвижностей катиона и аниона, т.е. их подвижностей при бесконечном разбавлении раствора.

На основании теории Дебая-Хюккеля Онзагером было предложено эмпирическое выражение [15]:

,

где коэффициенты  и  отражают наличие у ионов экранирующего облака, которое меняет их подвижность в силу двух различных эффектов.

Предельный закон Онзагера соблюдается только для крайне разбавленных растворов. В области высоких концентраций наблюдается отклонение от линейной зависимости.

Позднее Фуосс [16] теоретически получил уравнение, описывающее предельные эквивалентную электропроводность и вязкость раствора:

,

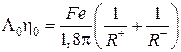где  и  – гидродинамические радиусы катиона и аниона. Эта зависимость подобна правилу Вальдена-Писаржевского:

.

До настоящего времени появляются теоретические и экспери­мен­тальные работы, посвященные определению предельных электропроводностей ионов [17, 18], концентрационной зависимости эквивалентной электропроводности водных растворов сильных электролитов [19], использующих в том или ином виде правило Вальдена-Писаржевского. В то же время наблюдаются существеннее противоречия в оценке ряда авторов выполнимости этого правила.

К другим направлениям усовершенствования теории электропроводности можно причислить работы [20-22]. Задача общей теории электропроводности электролитов заключается в предсказании изменения электропроводности в зависимости от размеров, заряда и других свойств ионов, молекул растворителя, а также условий опыта (температуры, давления и др.) в широком диапазоне изменения концентрации, температуры и сред.

А.А. Силковым с сотрудниками [23] получено линейное регрессионное уравнение, описывающее электропроводность растворов соли слабой кислоты, с помощью которого можно рассчитывать ее транспортные и тер­модинамические характеристики на основании уравнения электропро­водности, предложенного Робинсоном и Стоксом для разбавленных растворов одно-одновалентного электролита, и закона действующих масс.

Уравнения для зависимости эквивалентной электропроводности  от концентрации и частоты электрического поля получены с использованием теории сопряжения мод, которая применяется для описания транспортных свойств вблизи критической точки. Теория сопряжения мод позволяет установить связь между транспортными характеристиками индивидуального иона и коллективными динамическими свойствами электролита, в частности, его ионной атмосферой. Авторы [24] получили уравнение для зависимости  на основе частотной зависимости коэффициента диффузии. Недостатком данной работы является отсутствие корректного учета дисперсии электропроводности самого растворителя, вклад которой в ионное трение считается в данной работе постоянным, и, по мнению авторов, будет влиять при более высоких частотах. В результате наблюдается существенное отклонение от теории при высоких концентрациях и час­тотах. По существу, это численные методы с использованием подгоночных параметров.

Используя уравнение Ли-Уитона [25,26], Калугин и Панченко [27] предложили метод обработки кондуктометрических данных для растворов 1-1 электролитов с учетом образования ионных пар и тройников в средах с низкой диэлектрической проницаемостью. В результате авторам удалось расширить концентрационный диапазон использования уравнения Ли-Уитона вплоть до концентрации 3·10^–2 моль/л.

К сожалению, полученные результаты применимы лишь к элект­ро­литам в растворителях с диэлектрической проницаемостью, не превышающей 10 относительных единиц. Между тем большинство растворителей характерихуется более высокими значениями ДП. Кроме того, к числу ограничений метода можно также отнести необходимость использования значительного количества экспериментальных значений электропроводности (не менее 50).

Вызывают интерес работы, посвященные обнаружению предельной вы­сокочастотной электропроводности, величина которой обуславливается свойствами растворителя, а не электролита. В.И. Ермаковым с сотруд­ни­ками [28-30] предложена гипотеза об электронно-дырочной проводимости растворов электролитов, на основе механизма диэлектрической
релаксации.

Исследование электропроводности водных растворов электролитов в широком температурном диапазоне показало, что при высоких температурах наблюдается максимум на зависимости электропроводности – температура в водных [31-33], в неводных [34, 35] и в смешанных растворителях [36].

Ю.Я. Фиалков с сотрудниками [37,38] предложили уравнение, связывающее удельную электропроводность x с вязкостью , диэлектрической проницаемостью  и концентрацией раствора C:

,

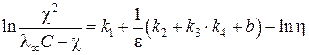где константы  определяются физико-химическими характеристиками растворителя. Использование авторами закона Оствальда для слабых электролитов при описании концентрированных растворов представляется сомнительным. Недостатком данного уравнения является также его применимость лишь для систем электролит – индифферентный растворитель.

В работах Балданова М.М. и других [39, 40] рассматривается состояние ионов в рамках концепции «ионной плазмы». Согласно современной теории плазменных процессов, Дебай и Хюккель ограничились лишь пространственной дисперсией и не придали значения частотной дисперсии, т.е. наличию в растворах электролитов продольных акустических колебаний совокупности ионов с частотой , аппроксимируемых как ионный звук. Балданов М.М с соавторами получили уравнение для расчета электропроводности  в виде:

,

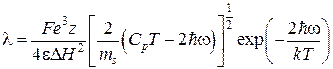здесь 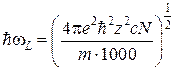 – энергия многочастичных коллективных взаимодействий ионов в растворах.

Предлагаемая трактовка состояния ионов электролитов позволяет с единых позиций объяснить такие факторы, как дисперсия электропровод­ности Дебая-Фалькенгагена, эффект Вина, максимальное значение электропроводности .

Так, при  получается выражение для предельной электропроводности:

.

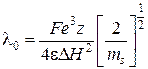Эффект Дебая-Фалькенгагена объясняется исходя из следующих представлений. Согласно функции диэлектрического отклика

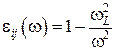
в области частот , где ω – частота внешнего поля, значение  отрицательна, что свидетельствует об эффективном притяжении ионов между собой, поскольку потенциальная энергия получается отрицательной. При  эффективное притяжение между ионами исчезает, что приводит к максимальному значению электропроводности , что и в слу­чае предельного разбавления.

Эффект Вина представлен следующим образом. При наложении внешнего поля E с энергией, равной потенциальной энергии коллективных межионных взаимодействий, являющейся вторым слагаемым в пред­став­ленном выше уравнении, ионы будут вести себя, так же как и в случае предельного разбавления. При этом электропроводность становится равной своему максимальному значению , а соответствующее значение напряженности поля E имеет вид:

.

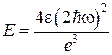Полученное авторами уравнение для теоретической оценки электрической проводимости объясняет λ практически во всем диапазоне концентраций, но только при 298К, поскольку значение энергии водородной связи растворителя в жидкой фазе известна лишь для этой температуры и равна  = 3,4 ккал/моль.

Таким образом, несмотря на определенные успехи в развитии теоретических представлений, проблема теоретического описания электрической проводимости растворов электролитов остается актуальной.