
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Дискретная оптимизация и моделирование в условиях неопределенности данных
Перепелица В. А., Тебуева Ф. Б.,
2.4. Методы типа покоординатного спуска для дискретных экстремальных задач.
В условиях неопределённости данных особого внимания заслуживают методы покоординатного спуска (градиентные алгоритмы) [83] по следующей причине. Если параметры задачи, например, в целевой функции (2.21) коэффициенты ![]()
![]() не являются действительными числами, а, допустим, являются интервалами [11] или нечеткими множествами [76], то эти алгоритмы можно использовать, заменяя операцию «поиск направления с максимальным (по абсолютной величине) числовым приращением целевой функции» на операцию «поиск наиболее предпочтительного направления». Иными словами, алгоритмы покоординатного спуска сохраняют свой принцип пошагового движения в «лучшем направлении» и в условиях неопределённости данных.
не являются действительными числами, а, допустим, являются интервалами [11] или нечеткими множествами [76], то эти алгоритмы можно использовать, заменяя операцию «поиск направления с максимальным (по абсолютной величине) числовым приращением целевой функции» на операцию «поиск наиболее предпочтительного направления». Иными словами, алгоритмы покоординатного спуска сохраняют свой принцип пошагового движения в «лучшем направлении» и в условиях неопределённости данных.
Описанный выше алгоритм решения задачи (2.22)-(2.23) относится к методам типа покоординатного спуска. Алгоритмы этого типа очень просты и малотрудоемки. Поэтому весьма интересно выявить класс задач, в которых искомый оптимум находится методом покоординатного спуска. В настоящем п.2.4 мы выделим один такой класс задач выпуклого (вогнутого) целочисленного программирования и установим признак разрешимости задачи из этого класса посредством алгоритма покоординатного спуска.
Обозначим через ![]() конечное множество целочисленных точек
конечное множество целочисленных точек ![]() , лежащее в положительном октанте
, лежащее в положительном октанте ![]() -мерного пространства
-мерного пространства ![]() и содержащее начало координат
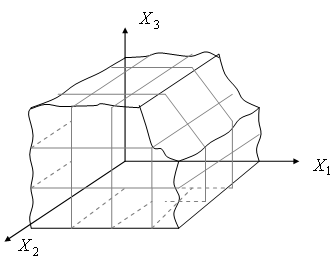
и содержащее начало координат ![]() . В целях наглядности, на рис.2.5 дано геометрическое представление множества P в 3-мерном пространстве
. В целях наглядности, на рис.2.5 дано геометрическое представление множества P в 3-мерном пространстве ![]() .
.
 .
.
Рисунок 2.5. Пример множества P в 3-мерном пространстве ![]() .
.
Рассмотрим следующий класс задач выпуклого целочисленного программирования с максимизирующей целевой функцией
![]() ,(2.24)
,(2.24)
у которой аргумент ![]() – это
– это ![]() -мерный целочисленный вектор и
-мерный целочисленный вектор и
![]() ,(2.25)
,(2.25)
где ![]() – выпуклые вверх (т.е. вогнутые) функции целочисленного аргумента
– выпуклые вверх (т.е. вогнутые) функции целочисленного аргумента ![]() .
.
Нашей целью будет исследование разрешимости задачи (2.24)-(2.25) посредством алгоритма покоординатного спуска (алгоритма ПС). Приведем неформальное описание этого метода.
Алгоритм ПС. Процесс вычислений начинается с точки ![]() .
.
Пусть после некоторого числа шагов мы пришли к точке ![]() . Следующий шаг состоит в переходе к такой точке
. Следующий шаг состоит в переходе к такой точке ![]() , которая:
, которая:
1) непосредственно следует за ![]() , т.е. отличается от
, т.е. отличается от ![]() лишь одной координатой
лишь одной координатой ![]() и
и ![]() ;
;
2) ![]() выбирается так, чтобы приращение
выбирается так, чтобы приращение ![]() было положительное и максимально возможное.
было положительное и максимально возможное.
Если такой точки ![]() не существует, то процесс заканчивается в точке
не существует, то процесс заканчивается в точке ![]() , если же их несколько, то выбирается любая из них. За конечное число шагов процесс заканчивается в некоторой точке
, если же их несколько, то выбирается любая из них. За конечное число шагов процесс заканчивается в некоторой точке ![]() . В этом случае будем говорить, что алгоритм приводит к точке
. В этом случае будем говорить, что алгоритм приводит к точке ![]() или
или ![]() есть результат применения алгоритма ПС на множество
есть результат применения алгоритма ПС на множество ![]() .
.
Вопрос (*): для каких множеств ![]() алгоритм ПС приводит к точке
алгоритм ПС приводит к точке ![]() , являющейся решением задачи (2.24)-(2.25) с целевой функцией
, являющейся решением задачи (2.24)-(2.25) с целевой функцией ![]() вида (2.25)?
вида (2.25)?
Иными словами, мы хотим обосновать критерий, который очертил бы по возможности более широкий круг задач, решаемых посредством алгоритма ПС. Для этого нам понадобятся в дальнейшем следующие обозначения:
1) ![]() –
– ![]() -мерные векторы с неотрицательными целочисленными компонентами;
-мерные векторы с неотрицательными целочисленными компонентами; ![]() означает, что компоненты векторов
означает, что компоненты векторов ![]() и
и ![]() удовлетворяют неравенствам
удовлетворяют неравенствам ![]() ,
, ![]() ;
;
2) ![]() ;
;
3) ![]() – вектор,
– вектор, ![]() -я компонента которого равна 1, а остальные
-я компонента которого равна 1, а остальные ![]() компонент равны нулю;
компонент равны нулю;
4) ![]() – множество допустимых направлений в точке
– множество допустимых направлений в точке ![]() относительно множества
относительно множества ![]() ;
;
5) ![]() – множество максимальных точек множества
– множество максимальных точек множества ![]() ;
;
6) ![]() ;
;
7) 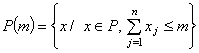 , при
, при ![]() ;
;
8) ![]() ,
, ![]() – множества максимальных точек множеств
– множества максимальных точек множеств ![]() и
и ![]() соответственно.
соответственно.
Рассмотрим значение целевой функции ![]() в точке
в точке ![]() и сравним его со значением в соседней точке
и сравним его со значением в соседней точке ![]() . Полученное приращение обозначим
. Полученное приращение обозначим
![]() .
.
Заметим при этом, что для функции ![]() вида (2.25) при выполнении неравенства
вида (2.25) при выполнении неравенства ![]() имеем
имеем ![]() ,
, ![]() . Согласно определению алгоритма ПС переход из точки
. Согласно определению алгоритма ПС переход из точки ![]() происходит в такую точку
происходит в такую точку ![]() , для которой
, для которой ![]() и
и ![]() .
.
Исчерпывающий ответ на поставленный выше вопрос (*) дает
Теорема 2.5. Для того, чтобы алгоритм ПС приводил к решению задачи (2.24)-(2.25) при любых ![]() вида (2.25), необходимо и достаточно, чтобы множество
вида (2.25), необходимо и достаточно, чтобы множество ![]() обладало двумя свойствами:
обладало двумя свойствами:
(А): если ![]() , то параллелепипед
, то параллелепипед ![]() ;
;
(B): для всякого вектора ![]() существует число
существует число ![]() такое, что из
такое, что из ![]() следует
следует ![]() .
.
Доказательство необходимости. Для того, чтобы доказать необходимость условия (А), предположим противное. Пусть ![]() и
и ![]() . Тогда найдутся точки
. Тогда найдутся точки ![]() и координата
и координата ![]() такие, что
такие, что ![]() ,
, ![]() ,
, ![]() .
.
Определим теперь целевую функцию![]() следующим образом:
следующим образом:
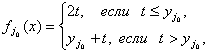 (2.26)
(2.26)
а для всех ![]() положим
положим
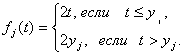 (2.27)
(2.27)
Если к целевой функции ![]() , определяемой соотношениями (2.26) и (2.27), применим алгоритм ПС, то в результате покоординатного спуска придем в точку
, определяемой соотношениями (2.26) и (2.27), применим алгоритм ПС, то в результате покоординатного спуска придем в точку ![]() . В то же время
. В то же время ![]() . Полученное противоречие доказывает необходимость условия (А).
. Полученное противоречие доказывает необходимость условия (А).
Доказательство необходимости условия (В) также проведем рассуждением от противного, т.е. предположим, что условие (В) нарушено следующим образом. Пусть для некоторого ![]() существуют точки
существуют точки ![]() и
и ![]() такие, что
такие, что ![]() и
и ![]() (т.е.
(т.е. ![]() и
и ![]() – максимальные точки из одного и того же множества
– максимальные точки из одного и того же множества ![]() ), но
), но ![]() ,
, ![]() и
и ![]() (т.е. указанного числа
(т.е. указанного числа ![]() , одинакового для всех
, одинакового для всех ![]() , не существует).
, не существует).
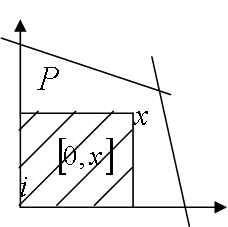
Положим теперь для определенности ![]() ,
, ![]() ,
,
Начиная с точки ![]() , будем искать оптимальное решение согласно определению алгоритма ПС. Согласно определению приращения
, будем искать оптимальное решение согласно определению алгоритма ПС. Согласно определению приращения ![]() вначале, продвигаясь в
вначале, продвигаясь в ![]() -мерном пространстве на каждом шаге на величину
-мерном пространстве на каждом шаге на величину ![]() , каждый раз получаем для
, каждый раз получаем для ![]() приращение
приращение ![]() . Поскольку считается, что наше множество
. Поскольку считается, что наше множество ![]() обладает свойством (А), то через
обладает свойством (А), то через ![]() шагов мы по необходимости придем в точку
шагов мы по необходимости придем в точку ![]() , в которой значение
, в которой значение ![]() . По условию точка
. По условию точка ![]() , т.е.
, т.е. ![]() – максимальная точка. Тогда попав в точку
– максимальная точка. Тогда попав в точку ![]() , мы из нее уже не выйдем. Действительно, если по направлению
, мы из нее уже не выйдем. Действительно, если по направлению ![]() имеем неравенство
имеем неравенство ![]() , то при попытке продвинуться на величину
, то при попытке продвинуться на величину ![]() , мы выйдем из множества
, мы выйдем из множества ![]() в силу максимальности точки
в силу максимальности точки ![]() . Если же
. Если же ![]() , то при попытке продвинуться на величину
, то при попытке продвинуться на величину ![]() мы выйдем из множества
мы выйдем из множества ![]() в силу
в силу ![]() .
.
Итак, в качестве окончательного решения мы придем к точке ![]() . В то же время по условию имеем
. В то же время по условию имеем ![]() , т.е.
, т.е. ![]() . Следовательно, решение
. Следовательно, решение ![]() – не является оптимальным, т.е. приходим к противоречию. Необходимость свойств (А) и (В) доказана.
– не является оптимальным, т.е. приходим к противоречию. Необходимость свойств (А) и (В) доказана.
Прежде, чем переходить к доказательству достаточности условий теоремы 1.5, отметим некоторые очевидные факты и докажем одну лемму.
Последовательность множеств ![]() является монотонно возрастающей и при достаточно больших
является монотонно возрастающей и при достаточно больших ![]() будет выполняться равенство
будет выполняться равенство ![]() .
.
Замечание 2.3. Если всё множество ![]() обладает свойствами (A) и (B), то этими свойствами обладают так же и множества
обладает свойствами (A) и (B), то этими свойствами обладают так же и множества ![]() ,
, ![]() . Кроме того, если
. Кроме того, если ![]() , то множество допустимых направлений
, то множество допустимых направлений ![]() . Следовательно, если
. Следовательно, если ![]() есть результат применения алгоритма ПС на множестве
есть результат применения алгоритма ПС на множестве ![]() , а
, а ![]() – предпоследняя точка на пути из 0 в
– предпоследняя точка на пути из 0 в ![]() , то имеем равенство
, то имеем равенство ![]() в случае
в случае ![]() . В противном случае
. В противном случае ![]() .
.
Лемма 2.1. Если ![]() ,
, ![]() и
и ![]() обладает свойством (В), то найдется индекс
обладает свойством (В), то найдется индекс![]() , для которого значение
, для которого значение ![]() .
.
Доказательство. В силу свойства (В) из условий леммы 2.1 следует неравенство ![]() . Предположим противное, т.е. что неравенство
. Предположим противное, т.е. что неравенство ![]() выполняется при любом индексе
выполняется при любом индексе ![]() . Определим вектор
. Определим вектор ![]() , положив
, положив ![]() ,
, ![]() . Тогда на множестве
. Тогда на множестве ![]() точки
точки ![]() и
и ![]() являются максимальными, что невозможно из-за выполнения свойств (В). Полученное противоречие завершает доказательство леммы 2.1.
являются максимальными, что невозможно из-за выполнения свойств (В). Полученное противоречие завершает доказательство леммы 2.1.
Продолжим доказательство теоремы 2.5.
Достаточность. Доказательство проведем для множеств ![]() методом индукции по
методом индукции по ![]() . При
. При ![]() утверждение тривиально. Предположим, что для множества
утверждение тривиально. Предположим, что для множества ![]() (
(![]() ) алгоритм ПС приводит к решению задачи. Пусть
) алгоритм ПС приводит к решению задачи. Пусть ![]() есть результат применения алгоритма ПС на множестве
есть результат применения алгоритма ПС на множестве ![]() .
.
Возможны два случая:
a) ![]() ;
;
b) ![]() .
.
Рассмотрим случай b). Пусть переход в точку ![]() произошел из точки
произошел из точки ![]() .Тогда эта точка
.Тогда эта точка ![]() является результатом применения алгоритма ПС на множестве
является результатом применения алгоритма ПС на множестве ![]() . По предположению индукции функция
. По предположению индукции функция ![]() достигает в точке
достигает в точке ![]() максимума на
максимума на ![]() . Кроме того, по определению алгоритма ПС приращение на последнем шаге
. Кроме того, по определению алгоритма ПС приращение на последнем шаге ![]() . Последнее означает, в частности, что
. Последнее означает, в частности, что ![]() .
.
Рассмотрим любую точку ![]() . По доказанной выше лемме 2.1 существует индекс
. По доказанной выше лемме 2.1 существует индекс ![]() , для которого выполняется неравенство
, для которого выполняется неравенство ![]() и, следовательно, в силу вогнутости функции
и, следовательно, в силу вогнутости функции ![]() выполняются соотношения
выполняются соотношения ![]() , т.е.
, т.е. ![]() . Отсюда, т.к.
. Отсюда, т.к. ![]() и в силу индукционного предположения в точке
и в силу индукционного предположения в точке ![]() достигается максимум.
достигается максимум.
Таким образом
![]() .
.
Это соотношение в произвольности выбора y означает, что ![]() достигает в
достигает в ![]() максимума на
максимума на ![]() . Теорема 2.5 доказана полностью.
. Теорема 2.5 доказана полностью.
Итак, мы установили необходимые и достаточные условия (А) и (В), при выполнении которых класс задач выпуклого или вогнутого целочисленного программирования можно решать экономным методом ПС. Спрашивается, насколько широк указанный класс? Наглядный ответ на этот вопрос можно дать, если обратиться к конкретному виду ограничений определяющих множество ![]() .
.
Ниже мы исследуем один класс, соответствующий случаю, когда множества ![]() определяются линейными соотношениями. Именно, рассмотрим множества
определяются линейными соотношениями. Именно, рассмотрим множества ![]() , определяемые неравенствами:
, определяемые неравенствами:
![]() ,
, ![]() ,(2.28)
,(2.28)
где ![]() ,
, ![]() и
и ![]() – целые неотрицательные числа. Удовлетворяющий этим условиям пример множества
– целые неотрицательные числа. Удовлетворяющий этим условиям пример множества ![]() для
для ![]() представлен на рис.2.6.
представлен на рис.2.6.
![]() Очевидно, что при любых
Очевидно, что при любых ![]() и
и ![]() множество
множество ![]() , определяемое условиями (2.28), содержит начало координат и обладает свойством (А) (если
, определяемое условиями (2.28), содержит начало координат и обладает свойством (А) (если ![]() , то и параллелепипед
, то и параллелепипед ![]() ).
).
 .
.
Рисунок 2.6. Пример множества P, удовлетворяющего условию (2.28) для ![]() .
.
Если каждая переменная ![]() входит хотя бы в одно ограничение (2.28), это множество
входит хотя бы в одно ограничение (2.28), это множество ![]() будет также и ограниченным, т.е. для любого
будет также и ограниченным, т.е. для любого ![]() существует
существует ![]() такое, что
такое, что ![]() .
.
Что касается свойства (В), то при произвольных ![]() и
и ![]() в (2.28) множество
в (2.28) множество ![]() этим свойством, вообще говоря, не обладает. Однако, можно указать такие дополнительные ограничения, налагаемые на матрицу
этим свойством, вообще говоря, не обладает. Однако, можно указать такие дополнительные ограничения, налагаемые на матрицу ![]() , при выполнении которых множество
, при выполнении которых множество ![]() будет обладать свойством (В) независимо от значений правых частей неравенств (2.28). С практической точки зрения именно этот случай представляет наибольший интерес.
будет обладать свойством (В) независимо от значений правых частей неравенств (2.28). С практической точки зрения именно этот случай представляет наибольший интерес.
Для формулировки указанных ограничений введем в рассмотрение множества ![]() ,
, ![]() , где
, где ![]() есть множество номеров
есть множество номеров ![]() всех переменных
всех переменных ![]() , входящих в
, входящих в ![]() -ое неравенство, т.е.
-ое неравенство, т.е. ![]() . Например, для матрицы
. Например, для матрицы ![]() эти множества имеют вид:
эти множества имеют вид: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Условимся, что в матрицах вида ![]() пустые клетки означают нули. Далее ради краткости будем говорить, что матрица
пустые клетки означают нули. Далее ради краткости будем говорить, что матрица ![]() имеет структуру типа дерева, если любые два множества
имеет структуру типа дерева, если любые два множества ![]() ,
, ![]() ,
, ![]() , таковы что, либо они не имеют общих элементов, либо одно из них включает другое. Например, матрица
, таковы что, либо они не имеют общих элементов, либо одно из них включает другое. Например, матрица ![]() имеет структуру типа дерева, а матрица
имеет структуру типа дерева, а матрица ![]() – не имеет, т.е.
– не имеет, т.е. ![]() ,
, ![]() и
и ![]() .
.
Теперь может быть сформулирована и доказана
Теорема 2.6. Для того, чтобы при фиксированных ![]() и произвольных
и произвольных ![]() определяемые неравенствами (1.28) множества
определяемые неравенствами (1.28) множества ![]() обладали свойством (В), необходимо и достаточно, чтобы матрица
обладали свойством (В), необходимо и достаточно, чтобы матрица ![]() имела структуру типа дерева.
имела структуру типа дерева.
Доказательство необходимости проведем рассуждением от противного. Пусть структура матрицы ![]() отлична от указанной в условиях теоремы. Тогда найдутся два множества, скажем
отлична от указанной в условиях теоремы. Тогда найдутся два множества, скажем ![]() и
и ![]() , такие, что ни одно из них не включает другое и
, такие, что ни одно из них не включает другое и ![]() . Пусть
. Пусть ![]() ,
, ![]() ,
, ![]() . Правые части неравенств (2.28) положим следующими:
. Правые части неравенств (2.28) положим следующими:
![]() и
и ![]() для всех
для всех ![]() (2.29)
(2.29)
и рассмотрим множество ![]() при
при ![]() .
.
Для этого множества максимальными являются следующие две точки: ![]() и
и ![]() , для которых
, для которых ![]() , то есть свойства (В) нарушено. Т.о., при указанных в (2.29) величинах
, то есть свойства (В) нарушено. Т.о., при указанных в (2.29) величинах ![]() множество
множество ![]() не обладает свойством (В).
не обладает свойством (В).
Необходимость доказана.
Достаточность. Пусть матрица ![]() имеет структуру типа дерева и
имеет структуру типа дерева и ![]() . Тогда множество
. Тогда множество ![]() , будучи ограниченным, имеет максимальные точки. Пусть
, будучи ограниченным, имеет максимальные точки. Пусть ![]() - максимальная точка.
- максимальная точка.
Номер ![]() назовем критическим, если
назовем критическим, если ![]() - траекторией ограничение системы (2.28) выполнятся в точке
- траекторией ограничение системы (2.28) выполнятся в точке ![]() как равенство, и для любого
как равенство, и для любого ![]() , такого, что
, такого, что ![]() ,
, ![]() -е ограничение выполняется как строгое неравенство.
-е ограничение выполняется как строгое неравенство.
В силу максимальности точки ![]() , для любого
, для любого ![]() существует критический номер
существует критический номер ![]() такой, что
такой, что ![]() . Пусть
. Пусть ![]() есть множество всех критических номеров
есть множество всех критических номеров ![]() . Тогда семейство множеств
. Тогда семейство множеств ![]() является разбиением множества
является разбиением множества ![]() на непересекающиеся подмножества, и, следовательно,
на непересекающиеся подмножества, и, следовательно, ![]() . Кроме того, для произвольной точки
. Кроме того, для произвольной точки ![]() имеет место неравенство
имеет место неравенство ![]() .
.
В частности, для любой максимальной точки ![]() имеем
имеем
![]() .
.
Поскольку ![]() ,
, ![]() в наших рассуждениях можно поменять местами, то нами доказано равенство
в наших рассуждениях можно поменять местами, то нами доказано равенство ![]() . Таким образом, существует число
. Таким образом, существует число ![]() такое, что для любой максимальной точки
такое, что для любой максимальной точки ![]() множества
множества ![]() имеет место равенство
имеет место равенство ![]() .
.
Рассмотрим теперь некоторое ![]() и к множеству
и к множеству ![]() , определяемому соотношением (2.28), добавим условия
, определяемому соотношением (2.28), добавим условия ![]() ,
, ![]() , в результате чего получим множество
, в результате чего получим множество ![]() . Доказанное утверждение остается справедливым и в этом случае, т.е. получим выполнение свойства
. Доказанное утверждение остается справедливым и в этом случае, т.е. получим выполнение свойства ![]() .
.
Теорема 2.6 доказана полностью.
Алгоритм покоординатного спуска чаще всего используется в качестве приближённых методов дискретной оптимизации.