Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
МЕТОДЫ ФОТОМЕТРИЧЕСКОГО АНАЛИЗА В САНИТАРНО-ГИГИЕНИЧЕСКИХ ИССЛЕДОВАНИЯХ
Дорогова В Б, Игнатьева Л П,
4.2.1. Определение и исключение грубых погрешностей (промахов)
В литературе приведены различные методы оценки и исключения грубых погрешностей. Рассмотрим два наиболее простых для практического использования метода.
Исключение грубых промахов по Q-критерию
При малых выборках с числом измерений п < 10 определение грубых погрешностей лучше оценивать при помощи размаха варьирования по Q-критерию. Для этого составляют отношение:
Q = |х1 – х2|R, (4.11)
|
где х1 – |
подозрительно выделяющийся результат определения (измерения); |
|
х2 – |
результат единичного определения, ближайший по значению к х1; |
|
R – |
размах варьирования, R = хmax –хmin разница между наибольшим и наименьшим значением. |
При малой выборке (n < 10) размах варьирования служит также одной из характеристик рассеяния результатов измерений.
Таблица 4.1
Значения – Q критерия в зависимости от пi и 
|
пi |
Доверительная вероятность |
||
|
0,90 |
0,95 |
0,99 |
|
|
3 |
0,89 |
0,94 |
0,99 |
|
4 |
0,68 |
0,77 |
0,89 |
|
5 |
0,56 |
0,64 |
0,76 |
|
6 |
0,48 |
0,56 |
0,70 |
|
7 |
0,43 |
0,51 |
0,64 |
|
8 |
0,40 |
0,48 |
0,58 |
Вычисленное значение Q сопоставляют с табличным значением Q (, пi) (табл. 4.1). Наличие грубой погрешности доказано, если Q > Q (, пi)
Исключение грубых погрешностей методом вычисления максимального относительного отклонения. Статистический критерий обнаружения грубых погрешностей основан на предположении, что выборка взята из генеральной совокупности, распределенной нормально. Это позволяет использовать распределение наибольшего по абсолютному значению нормированного отклонения:
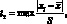(4.12)
где tт – теоретическое значение квантиля распределения статистики.
Для уровней значимости р = >>0,10; 0,05; 0,01 или доверительной вероятности 1 – р = 0,90; 0,95; 0,99 и п ? 25 значения tт приведены в табл. 4.2. Уровень значимости р = (1 – Р) – максимальная вероятность того, что погрешность превзойдет некое предельное (критическое) значение ±?xkj, т.е. такое значение, что появление этой погрешности можно рассматривать как следствие значимой (неслучайной) причины. На практике обычно используют уровень значимости р = 0,05 (результат получается с 95 %-й доверительной вероятностью).
Для того, чтобы в группе из п наблюдений х1 х2, ..., хп отбросить результат хmax (или хmin), надо:
а) вычислить дробь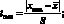 
б) по табл. 4.2 найти теоретическое значение tт в зависимости от п и выбранного уровня значимости р;
в) сравнить рассчитанное по п. «а» значение tmax с tт. Если tmax > tт, то результат tmax следует отбросить как промах.
Таблица 4.2
Значения квантилей распределения максимального отклонения,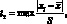
|
n |
Уровни значимости p |
n |
Уровни значимости p |
||||||
|
0,1 |
0,05 |
0,025 |
0,01 |
0,1 |
0,05 |
0,025 |
0,01 |
||
|
3 |
1,41 |
1,41 |
1,41 |
1,41 |
15 |
2,33 |
2,49 |
2,64 |
2,80 |
|
4 |
1,65 |
1,69 |
1,71 |
1,72 |
16 |
2,35 |
2,52 |
2,67 |
2,84 |
|
5 |
1,79 |
1,87 |
1,92 |
1,96 |
17 |
2,38 |
2,55 |
2,70 |
2,87 |
|
6 |
1,89 |
2,00 |
2,07 |
2,13 |
18 |
2,40 |
2,58 |
2,73 |
2,90 |
|
7 |
1,97 |
2,09 |
2,18 |
2,27 |
19 |
2,43 |
2,60 |
2,75 |
2,93 |
|
8 |
2,04 |
2,17 |
2,27 |
2,37 |
20 |
2,45 |
2,62 |
2,78 |
2,96 |
|
9 |
2,10 |
2,24 |
2,35 |
2,46 |
21 |
2,47 |
2,64 |
2,80 |
2;98 |
|
10 |
2,15 |
2,29 |
2,41 |
2,54 |
22 |
2,49 |
2,66 |
2,82 |
3,01 |
|
11 |
2,19 |
2,34 |
2,47 |
2,61 |
23 |
2,50 |
2,68 |
2,84 |
3,03 |
|
12 |
2,23 |
2,39 |
2,52 |
2,66 |
24 |
2,52 |
2,70 |
2,86 |
3,05 |
|
13 |
2,26 |
2,43 |
2,56 |
2,71 |
25 |
2,54 |
2,72 |
2,88 |
3,07 |
|
14 |
2,30 |
2,46 |
2,60 |
2,76 |
|||||
Процедуру исключения промахов можно повторить и для следующего по абсолютному значению максимального относительного отклонения, но предварительно необходимо пересчитать 
и s для выборки нового объема n – 1.