Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

МЕТОДЫ ФОТОМЕТРИЧЕСКОГО АНАЛИЗА В САНИТАРНО-ГИГИЕНИЧЕСКИХ ИССЛЕДОВАНИЯХ

Дорогова В Б, Игнатьева Л П,

4.4.2. Вычисление метрологических характеристик результатов анализа в случае линейной регрессии у = а + bх

4.4.2. Вычисление метрологических характеристик результатов анализа в случае линейной регрессии у = а + bх

Наличие уравнения линейной регрессии с числовыми значениями всех метрологических параметров при измеренных значениях аналитического сигнала анализируемой пробы (уан) позволяет перейти к расчету метрологических характеристик результатов анализа. хан – концентрации (содержанию) определяемого компонента, SXан – стандартного отклонения результата анализа; хан ± ?хан – доверительного интервала результата анализа; s – коэффициента чувствительности; предела обнаружения (в случае необходимости).

Однако при решении этих вопросов мы переходим от одной постановки математической задачи – от прямой линейной регрессии, когда при построении градуировочного графика погрешности х считались незначимыми –, к другой, обратно (сопряженной) линейной регрессии, когда погрешности определениях оказываются значимыми. Действительно, по заданному; значению зависимой случайной величины аналитического сигнала уан мы должны оценить соответствующее значение хан, которое по своей природе также является случайной величиной. При этом задача сводится к построению обратной (сопряженной) линии регрессии

x = c + dy (4.47)

и нахождению соответствующих доверительных границ хан, min и хан, max. Если бы уан не был бы случайной величиной, то уан был бы связан с хан обычной линейной функциональной зависимостью [см. уравнения (4.21)–(4.22)], откуда:

хан = (уан – а)/b (4.48)

или

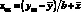(4.49)

и, имея серию хан1…, хан i…, хан n, обычными приемами можно было бы рассчитать основные метрологические характеристики результатов
анализа.

Однако ввиду разных постановок математических задач, которые приводят к двум различным линейным регрессиям[8] коэффициенты с ? а/b и d ? 1/b уравнения (4.22), (4.23) не являются алгебраическими, из которых непосредственно можно было бы найти хан ± ?хан.

4.4.2.1. Значение результата определяемой концентрации хан

Непременным условием дальнейшего применения линейной регрессии в количественном анализе является то, что определяемая концентрация компонента должна находиться в интервале концентраций, для которых рассчитано уравнение. При этих условиях измеряют значение аналитического сигнала уан анализируемого раствора и по преобразованным уравнениям (4.48) или (4.49) рассчитывают значение хан.

Чаще для повышения воспроизводимости результатов проводят m параллельных измерений значений аналитического сигнала или измерения уан1…, уан2…, yан m, для m ? 3 параллельных анализируемых проб.

Тогда

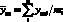(4.50)

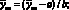(4.51)

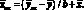(4.52)

4.4.2.2. Варианты расчета стандартного отклонения значения определяемой концентрации SXан

В случае градуировочного графика, выражаемого линейной регрессией у = а + bх, погрешность определения хан состоит из трех частных погрешностей, обусловленных погрешностями определения констант а, b и значения yaн (или 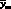). Эти три погрешности суммируются по закону накопления (закону распространения) ошибок, но конкретный вид выражения для расчета SXан зависит от методики построения градуировочного графика и измерения аналитического сигнала анализируемого раствора неизвестной концентрации.

Вариант 1. Градуировочный график строят по n стандартным растворам разной концентрации. Производят однократные измерения аналитического сигнала каждого стандартного раствора и однократное измерение yан. В этом случае для расчета SXан можно воспользоваться уравнением (4.29). Согласно закону накопления ошибок и исходя из уравнения (4.29), можно записать выражение для дисперсии

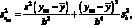(4.53)

где

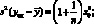
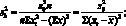
[согласно уравнению (4.37)].

Следовательно:

(4.54)

Вариант 2. Градуировочный график строят по п стандартным растворам разных концентраций, каждый из которых анализируют один раз, а раствор (проба) неизвестной концентрации анализируют из m параллельных определений и для расчета берут среднее значение аналитического сигнала

В этом случае, исходя из уравнения (4.52), в уравнении (4.53) член 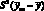будет равен:

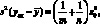(4.55)

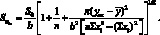
и тогда стандартное отклонение SXан будет рассчитываться из формулы:

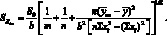(4.56)

Вариант 3. Градуировочный график строят по п стандартным растворам, каждый из которых анализируют m раз, и раствор (проба) неизвестной концентрации анализируют из m параллельных определений.

В этом случае расчет SXан проводят по формуле (4.56)), но вместо п подставляют значение п? = пт и расчеты значений у, x, b, s0 также ведут для п? = пт при и f???? = п’ – 2 = пт – 2.

Формула (4.54) может быть преобразована:

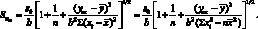(4.57)

Формула (4.56) может быть преобразована к виду:

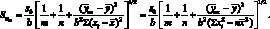(4.58)

Анализ формул (4.54) и (4.56) показывает:

1. Погрешность в определении неизвестной концентрации (значение SXан) зависит: от угла наклона графика (b); значения погрешности, обусловленной рассеянием точек относительно графика (s0); числа стандартных образцов (n), по которым строят график; числа параллельных измерений анализируемой пробы (m); расположения стандартных растворов (образцов) относительно и расположения анализируемой пробы относительно .

2. Стандартное отклонение результата определения SXан тем меньше, чем:

а) круче градуировочный график (чем больше значение коэффициента регрессии b[9];

б) больше число измерений п при построении градуировочного графика. В общем случае п должно быть не менее 5.

3. Для одного и того же градуировочного графика значение SXан различно для проб с разной концентрацией определяемого компонента. При больших разницах 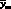(или уан) и  значение SXан возрастает. И наоборот: оно тем меньше, чем меньше эта разница, и минимально при 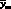(или уан) = . В этом частном случае третий член подкоренного выражения (4.54), (4.56) равен нулю; погрешность определения коэффициента регрессии sb не оказывает влияния на результаты определения хан, и значение SXан соответственно равно:

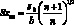(4.59)

или

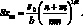(4.60)

4.4.2.3. Доверительный интервал значения определяемой концентрации

Величину ?хан рассчитывают по формуле:

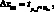(4.61)

где значение SXан вычисляют по одной из приведенных формул (4.54), (4.56). Значение коэффициента Стьюдента tP f, находят из табл. 4.3 при f = n – 2 или f = n’ – 2 в зависимости от варианта построения градуировочного графика и, как пpaвило, при Р = 0,95.

4.4.2.4. Интервальные значения определяемой концентрации

Интервальные значения определяемой концентрации оценивают по общей формуле:

хан ± ?хан. (4.62)[10]

Конкретный вид формулы (4.62) определяется вышерассмотренными вариантами построения и расчета градуировочного графика и измерения концентрации компонента в анализируемом растворе.

Вариант 1. Значение xaн рассчитывают по формулам (4.48) или (4.49); SXан – по формулам SXан (4.54), (4.57). Конечная формула для расчета интервальных значений определяемой концентрации имеет вид:

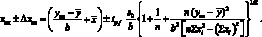(4.63)[11]

Варианты 2 и 3. Значение рассчитывают по формулам (4.51) или (4.52); SXан – по формулам (4.56), (4.58).Конечная формула для расчета интервальных значений определяемой концентрации имеет вид:

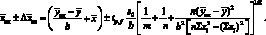(4.64)[12]

В тех практических случаях, когда 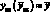, выражение в квадратных скобках значительно упрощается [см. формулы (4.59), (4.60)].

4.4.2.5. Пример расчета

Для определения бензола в этиловом спирте спектрофотометрическим методом анализа измерены оптические плотности семи стандартных растворов в УФ-области, по которым построен градуировочный график. Полученные результаты представлены в табл. 4.5. Далее проанализированы две серии двух растворов неизвестной концентрации бензола в спирте (по три параллельных пробы). По экспериментальным данным первой серии Аан1 = 1,52; Аан2 =  = 1,55; Аан3 = 1,53) рассчитано среднее значение , а для второй серии: . 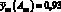Рассчитать значения 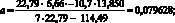и границы доверительного интервала.

Из данных табл. 4.5 получаем:

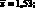
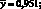(?хi)2 = 114,49; (?yi)2 = 44,36;

[п?хi2 – (?хi)2] = 7•22,79 – 114,49 = 58,9198[13];

?(хi + уi))2 = 22,79 + 2•13,850 + 8,4298 = 58,9198.

Таблица 4.5

Исходные данные и предварительные вспомогательные расчеты
при оценке параметров градуировочного графика

Далее рассчитываем параметры[14] линейного градуировочного графика, их метрологические характеристики и метрологические характеристики результатов анализа.

Параметр градуировочного графика Используемая формула

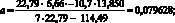(4.65)

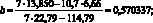(4.66)

SQ = (уi – Yi)2 = 8,429800 – 0,079628•6,66 – 0,570337•13,850 =
= 3,11•10–4; (4.67)

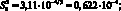(4.67)

(4.68)

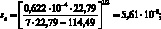(4.69)

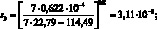(4.70)

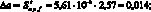
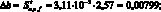
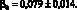(4.71)

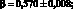(4.72)

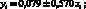(4.1) (4.2)

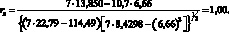(4.73)

Результат определения Используемая формула

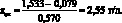(4.74)

При P = 0,95 и f = 5;

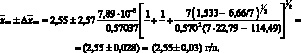(4.75)

Аналогичные расчеты для второй серии растворов с 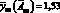 дают значение 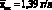. Так как в этом случае 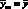, то третий член под корнем уравнения (4.75) становится мал и им можно пренебречь. Абсолютная погрешность определения 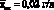будет меньше, чем в первом случае, и при Р = 0,95 границы доверительного интервала будут равны (1,39 ± 0,02) г/л.