Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Основы проектирования гидротехнических сооружений, лесных бирж и рейдов приплава
Седрисев Д Н, Рубинская А В, Аксёнов Н В, Кожевников А К,
7.5. Расчет элементов стальных конструкций по предельным состояниям первой группы
По первой группе предельных состояний рассчитывается несущая способность элементов стальных конструкций, т.е. прочность, устойчивость и выносливость при действии многократно повторяющейся нагрузки.
Строительные стали – это однородные материалы, напряженное состояние которых под нагрузкой хорошо подчиняется закону Гука. Поэтому формулы для их расчета по своей структуре – это формулы сопротивления материалов.
Расчет растянутых элементов. На центральное растяжение работают тяги, подвески, ряд элементов ферм с шарнирными узлами. Растягивающая сила N приложена в центре тяжести поперечного сечения стержня, напряжения равномерно распределены по сечению. Разрушение происходит от разрыва металла по наиболее ослабленному сечению, имеющему отверстия для болтов, заклепок и др.
Расчет прочности центрально растянутого элемента выполняется по формуле
σ = N1/An ≤ ycRy, (7.25)
|
где N1 – |
расчетное продольное усилие в сечении, кН, определяемое с учетом системы коэффициентов по формуле N1 = ynyfylcycaN; |
|
yn, yf, ylc, yca – |
соответственно коэффициенты надежности по назначению конструкции, по нагрузке, коэффициент сочетания нагрузок и дополнительный коэффициент условий работы, принимаемый в зависимости от причины разрушения стальных конструкций равным 0,7–1,0; |
|
Ап = А – Аω – |
площадь поперечного сечения нетто, см2, т. е. полная площадь А за вычетом площади ослабления Aw; |
|
ус – |
коэффициент условий работы, равный 0,7–1,1, учитывающий неблагоприятные влияния внешней среды и другие обстоятельства, не отражаемые в расчетах прямым путем; |
|
Ry – |
расчетное сопротивление стали растяжению по пределу текучести, МПа. |
Наименьшая площадь сечения центрально растянутого элемента, необходимая для обеспечения прочности,
An = N1/усRy, (7.25)
где N1 ус, Ry – то же, что и в формуле (7.25).
Затем по таблицам сортамента стали подбирается профиль, площадь поперечного сечения которого равна или немного больше Ап. Подбор сечения обычно завершается проверкой гибкости элемента.
Если растянутые элементы выполнить очень гибкими, например из
полосовой стали, то они могут иметь большие провисания. Согласно нормам,
гибкость λ = lef/i (отношение расчетной длины элемента к радиусу
инерции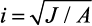 
растянутых элементов ферм, связей, находящихся под воздействием статической нагрузки) не должна превышать 400.
Если при растяжении нормальная сила N приложена с эксцентриситетом е по отношению к центру тяжести сечения, то в стержне, кроме продольной силы N, возникает также изгибающий момент M = Ne. При совместном действии N и М элемент подвергается внецентрениому растяжению и его прочность проверяется из условия:
σ = N1/An + М1/Wn ≤ усRy, (7.27)
|
где N1, An, уc, Ry – |
то же, что и в формуле (7.24); |
|
М1 – |
расчетный изгибающий момент в сечении, кНм, определяемый с учетом системы коэффициентов по формуле М1 = ynyfylc yca М; |
|
Wn – |
момент сопротивления сечения. |
Расчет сжатых элементов. Несущая способность сжатого элемента может быть исчерпана в результате того, что напряжение в конструкции достигло предела текучести (потеря прочности) или при напряжении в конструкции меньшем, чем предел текучести (потеря устойчивости). Для проверки этих двух совершенно различных по своей природе причин потери несущей способности необходимо выполнить расчет прочности и расчет устойчивости сжатого элемента.
Расчет прочности центрально сжатых и внецентренно сжатых элементов производится так же, как и расчет прочности центрально и внецентренно растянутых элементов соответственно по формулам (7.24) и (7.25).
Проверка устойчивости при центральном сжатии осуществляется по формуле
σ = N1/(φA) ≤ ycRy,
где φ – коэффициент продольного изгиба, учитывающий необходимость уменьшения расчетного сопротивления Ry во избежание выпучивания стержня и зависящий от гибкости элемента λ, и расчетного сопротивления стали Ry.
При проверке устойчивости внецентренно сжатых элементов следует учитывать, что потеря устойчивости может произойти в плоскости действия момента и из этой плоскости. Поэтому проверка устойчивости внецентренно сжатого элемента осуществляется по формулам:
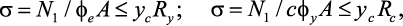(7.28)
|
где Nl, A, ус, Ry – |
то же, что и в формуле (7.25); |
|
φе – |
коэффициент продольного изгиба при внецентренном сжатии; |
|
φу – |
коэффициент центрального продольного изгиба, принимаемый в зависимости от гибкости |
Расчет изгибаемых элементов. Из курса сопротивления материалов известно, что в балке, подверженной изгибу, возникают нормальные σ, касательные τ, главные σmi напряжения. Кроме того, в местах приложения сосредоточенных сил в стенках балок возникают местные сжимающие напряжения σlос. При проектировании стального изгибаемого элемента необходимы проверка прочности по всем видам напряжений, расчет устойчивости, а также проверка жесткости элемента (второе предельное состояние).
Расчет на прочность элементов, изгибаемых в одной из главных плоскостей, выполняется по нормальным а и по касательным напряжениям по формулам:
(7.29)
|
где М1, Q1 – |
расчетные значения соответственно изгибающего момента, кН•м, и поперечной силы, кН; |
|
Wn – |
момент сопротивления сечения нетто, см3; |
|
Ry, Rs – |
расчетные сопротивления стали соответственно изгибу и сдвигу, МПа; |
|
S – |
статический момент полусечения относительно нейтральной оси, см3; |
|
J – |
момент инерции сечения относительно нейтральной оси, см4; |
|
tω – |
толщина стенки, см. |
Прочность стенки балки в местах приложения нагрузки к верхнему поясу, а также в опорных сечениях балки, не укрепленных ребрами жесткости, проверяется по формуле
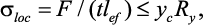(7.30)
|
где F – |
расчетное значение нагрузки (силы), кН; |
|
lef – |
условная длина распределения нагрузки, определяемая в зависимости от условий опирания. |
При совместном действии σ и τ материал балки находится в условиях сложного напряженного состояния. Для стенок балок должно выполняться условие
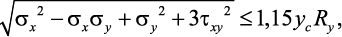(7.31)
|
где σх и σу – |
нормальные напряжения в срединной плоскости стенки, соответственно параллельные и перпендикулярные оси балки, МПа; |
|
τху – |
среднее касательное напряжение, – Q1/(th) МПа. Здесь t и h соответственно толщина и высота стенки, см; |
|
1,15 – |
коэффициент, учитывающий допустимость развития пластических деформаций на части стенки. |