Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Выглаживание: качество, технологии и инструменты

Губанов В Ф,

1.5.3. Спектральный анализ

При спектральном анализе [7], в первую очередь интерес представляют относительные колебания инструмента и заготовки (рис. 1.12). Здесь все сводится к поиску оптимальных (безвибрационных) режимов и условий обработки, обеспечивающих требуемые значения параметров качества и их регулярность при наименьшем износе инструмента. Следует отметить, что, измерив, например, колебания инструмента при обработке, из них необходимо отнять вынужденные колебания инструмента при холостом ходе (в принципе их не должно быть на станках повышенной точности). Таким образом, получим новую случайную функцию (амплитуда-время) как разность двух синхронизированных функций, наблюдаемых на выходе системы, на входе которой измеряется сила выглаживания. Если процесс обработки заготовки занимает «длительное» время, полезно, через определенные промежутки времени, оценивать следующие параметры: пик-фактор, показывающий, во сколько раз максимальное значение превосходит среднеквадратичное отклонение амплитуды; коэффициент вариации, характеризующий степень рассеяния амплитуды относительно ее математического ожидания; коэффициент асимметрии распределения. Значительное изменение указанных характеристик будет свидетельствовать о перераспределении энергии флуктуации амплитуд, т.е. о появлении редких высоких пиков, следовательно, в этом случае, процесс обработки не будет стабильным. По виду изменения указанных характеристик во времени и их значениям можно, например, установить, образуется ли регулярный профиль шероховатости поверхности и т.д.

В общем случае амплитудно-модулированный вибросигнал y(t) в виде квазиполигармонического процесса можно представить известной зависимостью:

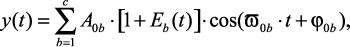(1.28)

где A0, ϖ0, φ0 – амплитуда, частота и фаза несущего вибросигнала; E(t) – шумовая компонента с равномерным спектром, которая обуславливается влиянием нестабильности температуры в зоне выглаживания, вязкостью СОТС, неравномерной твердостью выглаживаемой детали и другими факторами.

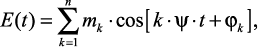(1.29)

где ψ, φ – частота и фаза модулирующего гармонического сигнала, mk – парциальный индекс амплитудной модуляции, m_k = E_k/A₀.

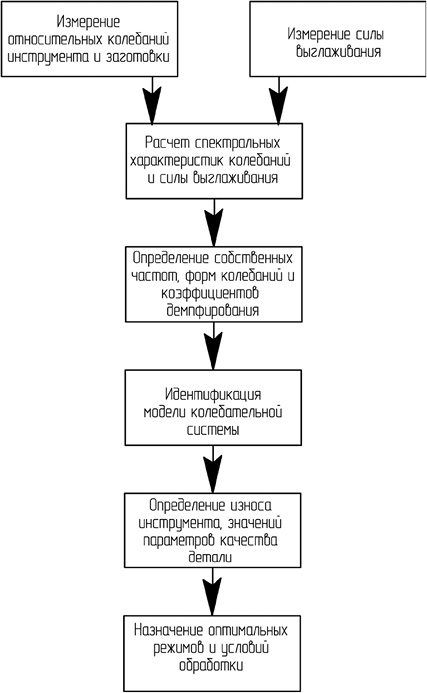
Рис. 1.12. Задачи спектрального анализа при выглаживании деталей

В вибросигналах из зоны выглаживания обычно присутствует три несущих вибросигнала (с = 3), модулируемых шумовой компонентой. Именно эти несущие вибросигналы (их амплитуды, частоты и фазы) представляют наибольший интерес для вибродиагностики параметров качества деталей в ходе процесса выглаживания [18, 24].

Следует отметить, что износ индентора, дефекты на поверхности заготовки, нарушающие стабильность процесса выглаживания, приводят к увеличению глубины модуляции. Обычно мощность (амплитуда) несущей частоты (собственной резонансной частоты процесса) больше чем мощность периодического (модулирующего) вибросигнала и ее обнаружение (выделение) не представляет затруднений. Из сказанного выше очевидно, что несущий вибросигнал представляет собой следствие процессов, формирующих стационарные значения параметров качества выглаженной поверхности детали, а модулирующий сигнал – следствие процессов, накладывающих «случайную» компоненту на стационарные параметры качества. По выделенному модулирующему сигналу таким образом можно судить о «дефектах» (износ индентора, неравномерность свойств выглаживаемой заготовки) процесса выглаживания.

Следовательно, все стандартизованные значения параметров качества деталей (например, микротвердость) формируемые в процессе выглаживания, которые, в большинстве случаев, являются средними значениями, с достаточной точностью могут быть описаны параметрами несущего вибросигнала (вибросигналов).