Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Теоретическое моделирование магнитоэлектрического эффекта в магнитострикционно-пьезоэлектрических наноструктурах

Бичурин М И, Петров В М,

1.2. Низкочастотный магнитоэлектрический эффект в двухслойных наноструктурах на подложке

Этот раздел работы посвящен моделированию МЭ эффекта в феррит-пьезоэлектрической двухслойной наноструктуре на подложке.

Мы выбрали в качестве модели структуру ФН-ЦТС. Известно, что пьезомагнитная связь, которая важна для получения сильного МЭ взаимодействия, является результатом магнитострикции с учетом наличия подмагничивающего поля и определяется постоянной магнитострикции и магнитной проницаемостью. Хотя ФН обладает слабой магнитострикцией по сравнении с ферритом кобальта, эта структура имеет более сильный пьезомагнитный эффект вследствие высокой магнитной проницаемости.

Таким же образом ЦТС обладает более сильным пьезоэлектрическим эффектом, чем титанат бария. Мы рассматриваем наноструктуры, выращенные на подложках из MgO. Этот материал больше всего подходит экспериментально, так как он химически инертен, и его кристаллическая решетка соответствует решетке сегнетоэлектрических и ферромагнитных компонент. МЭ коэффициент по напряжению α_E измеряется для ориентации полей, соответствующих минимальным размагничивающим полям и максимальному значению α_E. Влияние зажатия подложки описывается с помощью зависимости αE от размеров подложки и образца или их объемных долей [23, 25–26]. В случае двухслойных структур αE экспоненциально снижается по мере увеличения объемной доли MgO. Для столбчатой наноструктуры из ФН в матрице ЦТС влияние закрепления подложки тем меньше, чем больше соотношение длины стержней к их радиусам.

Для оценки αE принято, что пьезоэлектрическая фаза электрически поляризована в постоянном электрическом поле Е, а к композиту прикладывается подмагничивающее Н и переменное магнитное поле δН, вызывая при этом пьезомагнитные деформации. Затем мы решаем уравнения магнитостатики и эластостатики для ФН, и уравнения электростатики и эластостатики для ЦТС с учетом соответствующих граничных условий. Для определения МЭ восприимчивости нанокомпозит рассматривается как гомогенная среда, обладающая эффективными материальными параметрами, которые связывают напряжения, деформации, электрическое, магнитное поля и индукции. Затем рассчитывается МЭ коэффициент по напряжению как отношение МЭ восприимчивости к диэлектрической проницаемости. Модель можно использовать для оценки МЭ коэффициентов через известные материальные параметры (пьезоэлектрические коэффициенты, коэффициенты магнитострикции, жесткость и др.) или для определения параметров композита по данным измерений.

Для поляризованной пьезоэлектрической фазы с симметрией ¥m, магнитострикционной фазы с кубической симметрией и подложки могут быть записаны следующие выражения для деформации, электрического и магнитного смещения:

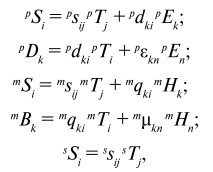  (9)

где Si и Tj – компоненты тензоров деформации и напряжения, Ek, Dk, Hk и Bk – компоненты вектора электрического поля, электрического смещения, магнитного поля и магнитной индукции, sij, dki, и qki – эффективная податливость, пьезоэлектрический и пьезомагнитный коэффициенты, а εkn и μkn – матрицы диэлектрической проницаемости и магнитной проницаемости. Индексы p, m и s соответствуют пьезоэлектрической, магнитострикционной фазам и подложке.

Следующим этапом является рассмотрение нанокомпозита в качестве гомогенной среды. При этом средние значения Si, Tj, Ek, Hk, Dk, и Bk определяются как:

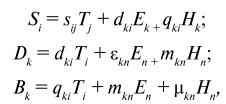(10)

где sij, dki, и qki – эффективные податливость, пьезоэлектрический и пьезомагнитный коэффициенты, а εkn, μkn и mkn – эффективная диэлектрическая проницаемость, магнитная проницаемость и МЭ коэффициент. Уравнения (10) с учетом уравнений (9), позволяют определить все эффективные параметры, фигурирующие в уравнениях (10).

Моделирование МЭ эффекта в слоистых системах феррит-ЦТС показало, что αE должен иметь максимальное значение в случае продольных «в плоскости» полей, т.е. постоянное магнитное поле и переменные электрическое и магнитное поля прикладываются параллельно друг другу в плоскости образца [23]. Для продольной и поперечной ориентаций полей ожидается, что αE будет иметь меньшие значения вследствие более слабых пьезомагнитного и пьезоэлектрического эффектов, а также размагничивающих полей. Эти результаты моделирования полностью соответствуют экспериментальным данным. Таким образом, оценки αE для двухслойной структуры ФН-ЦТС на подложке из MgO ограничены использованием продольных«в плоскости» полей. Примем следующую координатную систему, в которой образец находится в плоскости (1,2).

Пьезоэлектрическая фаза поляризована в электрическом поле E, направленного вдоль оси 1, при этом постоянное магнитное H1 и переменное магнитное δH1 поля прикладывается вдоль оси 1. Результирующее переменное электрическое поле измеряется вдоль этого направления для определения МЭ коэффициента по напряжению αE,11 = δE1/δH1. Для решения систем уравнений (9) и (10) воспользуемся следующими граничными условиями:

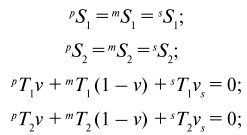  (11)

где v = pv/(pv + mv), vs = sv/(pv + mv), а pv, mv и sv – объемные доли пьезоэлектрической, магнитострикционной фаз и подложки, соответственно.

МЭ коэффициент по напряжению численно рассчитывается из уравнений (9)–(11) при использовании условия разомкнутой цепи D1 = 0. На рис. 3 показана зависимость МЭ коэффициента по напряжению от объемной доли ЦТС для структуры ФН-ЦТС на MgO, которая построена для материальных параметров из табл. 1. Для свободно опертой двухслойной наноструктуры αE,11 увеличивается по мере увеличения объемной доли ЦТС, достигает максимального значения в 1,6 В/см Э при v = 0,11 и затем быстро снижается при дальнейшем увеличении v. Следует отметить, что наблюдается уменьшение αE,11 на два порядка, если поместить пленку на тонкую подложку MgO с объемной долей равной 50 % от объемной доли пленки. Как видно из рис. 3, дальнейшее увеличение vs приводит к существенному уменьшению αE,11, а МЭ эффект практически исчезает, если пленка будет на подложке из MgO с объемной долей 10 и более. На рис. 4 показана зависимость максимального значения ME коэффициента по напряжению αE,11max и соответствующей объемной доли ЦТС vmax от объемной доли подложки vs. Увеличение объемной доли ЦТС, соответствующей максимальному МЭ эффекту, обусловлено изменением эффективной податливости образца с возрастанием толщины подложки.  

Рис. 3. Расчетная зависимость продольного в плоскости MЭ коэффициента по напряжению αE,11 = δE1/δH1 для двухслойной структуры ФН-ЦТС
от объемной доли ЦТС для серии объемных долей vs подложки из MgO

Таблица 1

Материальные параметры ЦТС, феррит кобальта (ФК),
титаната бария (ТБ), феррита никеля (ФН), MgO и SrTiO3, используемых для теоретических оценок

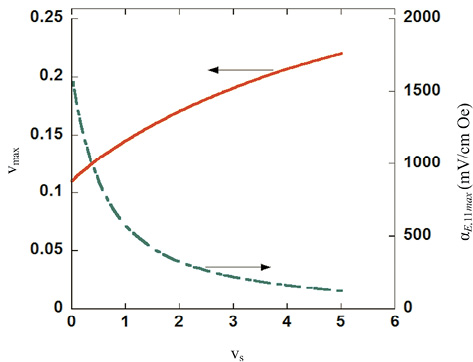
Рис. 4. Зависимость максимального значения ME коэффициента
по напряжению αE,11max и соответствующей объемной
доли ЦТС vmax от объемной доли подложки vs