
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.4. Эффект несоответствия кристаллических решеток наноструктуры и подложки
Известно, что несоответствие кристаллических решеток подложки и пьезоэлектрического слоя приводит к изменению пьезоэлектрического коэффициента и диэлектрической проницаемости. Эти изменения могут быть найдены, используя феноменологическую термодинамическую теорию Ландау-Гинзбурга-Девоншира [30]. Согласно этому методу, термодинамический потенциал G′ для тонкой пленки по толщине подложки определяется как
G´ = G + Ss1Ts1 + Ss2Ts2 + Ss6 Ts6, (15)
где G является функцией Гиббса для ЦТС слоя без подложки, SS1, SS2 и SS6 – компоненты деформации на границе раздела между пленкой и подложкой, возникающие из несоответствия кристаллических решеток; Ts1, Ts2 и Ts6 – компоненты остаточных напряжений. В случае (001) для сегнетоэлектрических тонких пленок, выращенных в кубической параэлектрической фазе на кубической (001) подложке, выражение для G выглядит следующим образом:
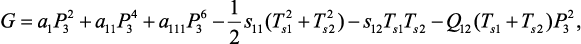 (16)
(16)
где a1, a11 и a111 – сегнетоэлектрические жесткости, Q12 – константа электрострикции.
Компоненты напряжений могут быть найдены с помощью соотношений: ∂G/∂Ts1 = –Ss1 и ∂G/∂Ts2 = –Ss2. Принимая во внимание, что S6 = 0 и S1 = S2 = Sm, спонтанную деформацию можно вычислить через параметр решетки подложки b и эквивалентную постоянную кубической решетки a0 свободной пленки: Sm = (b - a0)/b. Для пленки ЦТС на подложке SrTiO3 a0 = 0,397 нм и b = 0,393 нм. С помощью этих уравнений с параметрами [31] для функции Гиббса можно определить диэлектрическую проницаемость и пьезоэлектрический коэффициент ЦТС: pε11/ε0 = 51, pd31 = -18 pm/V. Аналогичным образом, пьезомагнитные параметры пленки ФН должны быть меньше, по сравнению с объемным ФН. Тем не менее, в структуре ФН – ЦТС – SrTiO3 нижний слой ЦТС действует как буферный слой и эффективно снижает зажатие со стороны подложки, в результате сжимающие деформация в слое ФН становятся пренебрежимо малыми [31]. В дальнейшем мы пренебрегаем вкладом остаточных деформаций в слое ФН, возникающие от несоответствия кристаллических решеток.
Подставляя соответствующие значения свойств материала и размеров структуры в уравнение (14), можно найти МЭ коэффициент по напряжению для двухслойных структур на подложке.
Согласно нашей модели наблюдается уменьшение МЭ коэффициента по напряжению для свободной двухслойной структуры по сравнению со случаем, когда не учитываются изгибные деформации, что связано с искривлением образца и уменьшением продольных деформаций пьезоэлектрического слоя. Размещение двухслойной структуры на подложке приводит к увеличению ME коэффициента с ростом толщины двухслойной структуры из-за вклада изгибных деформаций в общую деформацию ЦТС по сравнению со свободной двухслойной структурой. Дальнейшее увеличение vs приводит к существенному уменьшению ME коэффициента, как показано на рис. 6. Тем не менее, скорость изменения αE,31 оказывается значительно ниже, чем в случае, когда не учитываются изгибные деформации. Это может быть объяснено меньшей силой, которая необходима для изгибных деформаций структуры на подложке, чем для продольных деформаций.
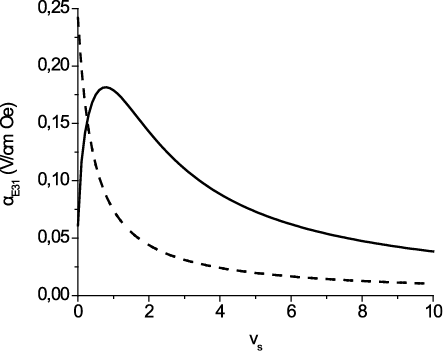
Рис. 6. Зависимость МЭ коэффициента по напряжению aE,31 для
структуры ФН-ЦТС на подложке из SrTiO3 от отношения толщины подложки
к толщине двухслойной структуры vs для v = 0,6, рассчитанная по
формуле (14)
(сплошная линия) и с использованием модели продольных
деформаций (прерывистая линия)
Следует отметить, что экспериментально измеренный ME эффект в двухслойной наноструктуре ФН – BaTiO3 на подложке из SrTiO3 [31] превышает теоретическое значение. Природа этого явления нуждается в уточнении.
