
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.1. Влияние постоянного электрического поля на магнитную восприимчивость
Данный раздел посвящен влиянию постоянного электрического поля на магнитную восприимчивость. Теория предсказывает резонансную зависимость магнитной восприимчивости от электрического поля. Далее рассматривается методика вычисления МЭ коэффициентов с учетом влияния подложки и изгибных деформаций образца.
Изучение высокочастотной восприимчивости композита имеет важное значение для практического использования МЭ эффекта. Взаимодействие электрической и магнитной подсистем в композите может быть описано путем введения MЭ восприимчивости. В общем случае, МЭ восприимчивость определяется следующими соотношениями [43, 45].
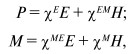 (29)
(29)
где Р – электрическая поляризация; М – намагниченность;
Е
и Н – напряженности внешних электрического и магнитного полей, cE и cM –
электрическая и магнитная восприимчивости, а cEM и cME – МЭ
восприимчивости, причем 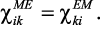 Р, М, Е и Н в (29), как правило, содержат переменную и постоянную составляющие. Например,
P = P0 + p exp(iωt).
Р, М, Е и Н в (29), как правило, содержат переменную и постоянную составляющие. Например,
P = P0 + p exp(iωt).
Для СВЧ диапазона МЭ восприимчивость определяется выражениями:
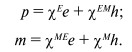 (30)
(30)
В уравнении (30) восприимчивости зависят от постоянных полей. Рассмотрим тензор магнитной восприимчивости композита, в который вносит вклад MЭ взаимодействие [41, 42, 43]. Образец подвергается влиянию постоянных электрического и магнитного полей и переменного магнитного поля. Плотность термодинамического потенциала можно записать в виде:
W = W0 + WМE, (31)
где W0 – плотность термодинамического потенциала при Е = 0, а
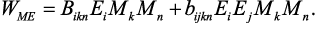 (32)
(32)
где Bikn и bijkn– линейная и билинейная MЭ константы, соответственно. Число независимых составляющих определяется структурой материала. Для поляризованных композитов основной вклад в WМE вносит линейная MЭ константа Bikn. Если композит не поляризован, то билинейная MЭ константа является доминирующей. Обе MЭ константы (линейная и билинейная) важны, если композит поляризован частично [45]. Воспользуемся методом эффективных размагничивающих факторов [45], чтобы решить линейное уравнение движения намагниченности и получить следующее выражение для магнитной восприимчивости:
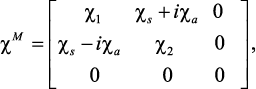 (33)
(33)
где
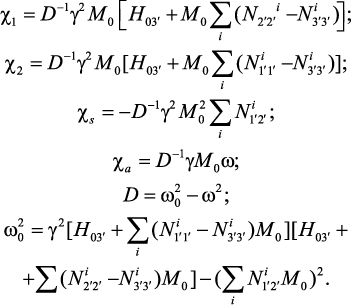
Здесь γ – магнитомеханическое отношение; ω – угловая частота;
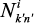 –размагничивающие факторы, описывающие эффективные поля магнитной
анизотропии, 1′, 2′, 3′ является системой координат, в которой ось 3′
направлена вдоль равновесной намагниченности. В уравнении (33)
суммирование ведется по всем видам магнитной анизотропии. MЭ
взаимодействие соответствует дополнительному слагаемому (i = Е) [49,
50].
–размагничивающие факторы, описывающие эффективные поля магнитной
анизотропии, 1′, 2′, 3′ является системой координат, в которой ось 3′
направлена вдоль равновесной намагниченности. В уравнении (33)
суммирование ведется по всем видам магнитной анизотропии. MЭ
взаимодействие соответствует дополнительному слагаемому (i = Е) [49,
50].
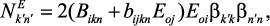 (34)
(34)
где β является матрицей направляющих косинусов осей (1′, 2′, 3′) по отношению к кристаллографической системе координат (1, 2, 3).
Следует отметить, что в уравнении (33) , поскольку предполагается,
что образец намагничен постоянным полем до насыщения (до образования
одного домена). Используя уравнение (33), легко заметить, что сдвиг
резонансной линии при приложении электрического поля можно выразить
в линейном приближении по 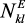 :
:
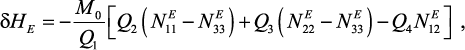 (35)
(35)
где
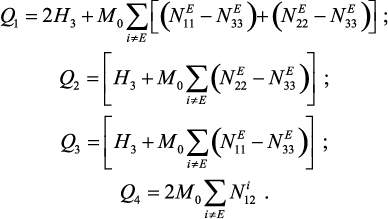
Уравнение (35) позволяет определить МЭ константы композита и, следовательно, интерпретировать полученные данные о резонансном ME эффекте. Далее находим общее выражение для тензора магнитной восприимчивости феррит-пьезоэлектрического композита, рассматривая структуру с симметрией 3m или 4mm. В этом случае уравнение (32) имеет вид:
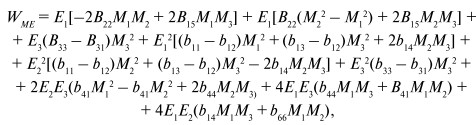 (36)
(36)
где b66 = (b11 – b12)/2 для точечной группы симметрии 3m и B22 = b14 = b41 = 0 для 4mm. Будем считать, что матрица направляющих косинусов имеет вид
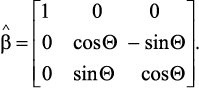 (37)
(37)
где Θ – угол между равновесной намагниченностью и осью симметрии кристалла. Рассмотрим образец в форме диска в базисной плоскости с одноосной магнитной анизотропией. В этом случае получаем из уравнений (34), (35) и (36):
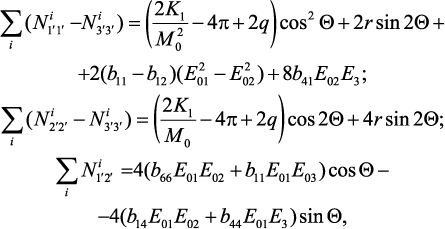 (38)
(38)
где

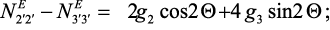
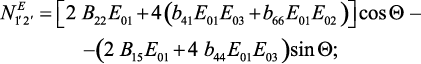
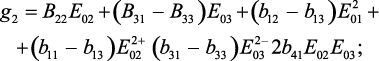
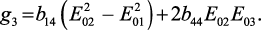
Подставляя выражение (37) в уравнение (34) можно получить выражение для компонентов тензора магнитной восприимчивости.
Рассмотрим
частный случай электрического поля, направленного вдоль оси симметрии
структуры, т. е. Е01 = 0 = Е02, Е03 = E0 и получим
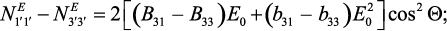
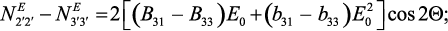 (39)
(39)
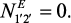
Для дискового образца, намагниченного вдоль оси симметрии, уравнения (5) и (39) запишутся в виде
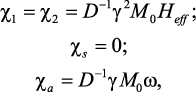 (40)
(40)
где
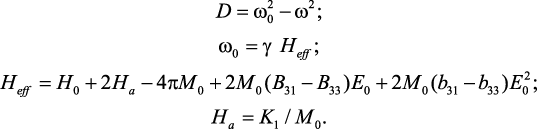
Положим, что потери энергии в уравнении движения намагниченности записываются как iwa(M0•m)/M0, где a – параметр диссипации. Тогда компоненты тензора магнитной восприимчивости являются комплексными величинами:
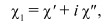
где
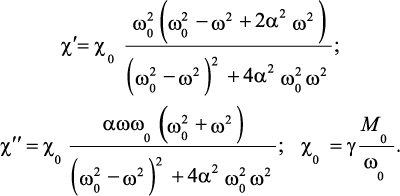 (41)
(41)
Как следует из формул (33) и (40), зависимость магнитной восприимчивости от внешнего постоянного электрического поля имеет резонансный характер. Характер этой зависимости можно объяснить тем, что посредством MЭ взаимодействия внешнее электрическое поле приводит к изменению эффективного магнитного поля Heff в уравнении (40)
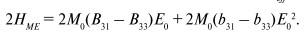
Изменение возникает благодаря механической связи пьезоэлектрической и магнитострикционной фаз, и феноменологически описано MЭ константами Bikn и bijkn в формулах (3) и (4). Таким образом, изменение внешнего постоянного электрического поля действует так же, как изменение магнитного поля и приводит к резонансной зависимости. Выражения для компонентов восприимчивости могут быть получены с помощью размагничивающих факторов, в соответствии с уравнением (33).
Теперь рассмотрим конкретные композиты и оценим магнитную восприимчивость и ее изменение во внешнем электрическом поле. Три композита: феррит лития (ФЛ)-ЦТС, феррит никеля (ФН)-ЦТС, железоиттриевый гранат (ЖИГ)-ЦТС – имеют важное значение для возможного практического использования. Рассмотрим простую двухслойную структуру, состоящую из монокристаллического феррита и ЦТС. Для получения выражения для магнитной восприимчивости требуется знание MЭ констант и параметра потерь α. МЭ константы могут быть оценены с помощью коэффициентов жесткости, константы пьезоэлектрической связи, магнитострикции и намагниченности для двух фаз, как описано в нашей предыдущей работе [50]. Предположим, что оси пьезоэлектрической фазы совпадает с осью [100] магнитострикционной фазы и ¦λ100¦ = 1,4•10–6, 23•10–6 и 46•10–6 для ЖИГ-ЦТС, ФЛ-ЦТС и ФН-ЦТС соответственно. Тогда получим 2M0(B31 – B33) = 0,1; 0,6 и 1,4 Э•см/кВ для этих трех образцов. Коэффициенты жесткости и намагниченности насыщения для ЖИГ-ЦТС и НФ-ЦТС, используемые в расчетах, имеют такое же значение, как и в [40]. Для ФЛ используются следующие параметры: mc11 = 24,47•1010 Н/м2; mc12 = 13,71•1010 Н/м2; mc44 = 9,36•1010 Н/м2; 4pMs = 3600 Гс. Параметры потерь для ЖИГ-ЦТС, ФЛ-ЦТС и ФН-ЦТС полагаются равными α = 0,025; 0,05 и 0,075 соответственно.
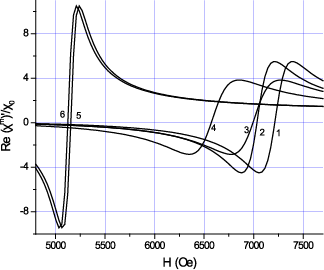
Рис. 17 показывает зависимость действительных и мнимых частей
магнитной восприимчивости от статического магнитного поля для слоистых
образцов ФЛ-ЦТС, ФН-ЦТС и ЖИГ-ЦТС. Результаты указаны для двухслойного
диска на частоте 9,3 ГГц для перпендикулярно направленных полей Н и Е.
Диапазон статического поля выбирается так, чтобы включить в него ФМР
в феррите. При приложении E = 300 кВ/см
наблюдается сдвиг
резонансного магнитного поля в сторону меньших значений. Величина сдвига
определяется МЭ константами, которые в свою очередь, сильно зависят от
констант магнитострикции. Большая
магнитострикция ФН приводит
к относительно сильному сдвигу резонансного поля, индуцированному
электрическим полем, в структуре ФН-ЦТС по сравнению с ЖИГ-ЦТС. Сдвиг
также связан с шириной резонансной линии. Это может быть объясняется
тем, что ширина резонансной линии зависит от эффективного поля
анизотропии, которое зависит от магнитострикции.
a б
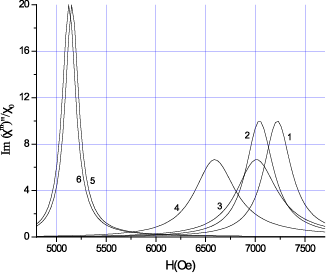
Рис. 17. Теоретическая зависимость действительной (а) и мнимой(б)
частей магнитной восприимчивости от подмагничивающего поля для
двухслойных структур ФЛ-ЦТС (кривые 1 и 2), ФН– ЦТС (кривые 3 и 4)
и ЖИГ– ЦТС (кривые 5 и 6) для частоты 9,3 GHz.
Кривые 1, 3 получены при E = 0, кривые 2, 4 – для E = 300 kV/cm.
Рис. 18 показывает расчетные действительную и мнимую части магнитной восприимчивости как функции приложенного электрического поля на частоте 9,3 ГГц. Постоянное магнитное поле устанавливается равным резонансному полю. Таким образом, рис. 18 иллюстрирует резонансную зависимость компонентов магнитной восприимчивости от постоянного электрического поля. Ширина резонанса измеряется в единицах электрического поля и обратно пропорциональна параметру 2M0(B31 – B33). Как следует из уравнения (40), узкий резонанс свидетельствует о сильном МЭ эффекте в композиционных материалах. В частности, двухслойная структура ФН-ЦТС показывает более узкую резонансную линию, чем структура ЖИГ-ЦТС. Рис. 17 и 18 представляют собой магнитные спектры композитов, полученные при использовании соответственно магнитной и электрической разверток.
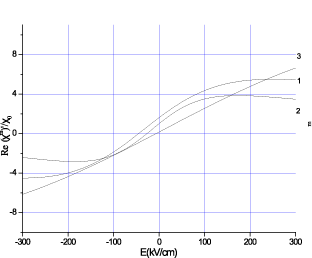

а б
Рис. 18. Теоретическая зависимость действительной (а) и мнимой(б) частей магнитной восприимчивости от постоянного электрического поля для двухслойных структур ФЛ-ЦТС (кривые 1 и 2), ФН– ЦТС (кривые 3 и 4) и ЖИГ– ЦТС (кривые 5 и 6) для частоты 9,3 GHz. Кривые 1, 3 получены при E = 0, кривые 2, 4 – для E = 300 kV/cm
