Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Бичурин М И, Петров В М,
4.2. Расчет магнитоэлектрических коэффициентов
В качестве примера рассмотрим простую модель, например, двухслойную, состоящую из феррита с кубической (m3m) симметрией и поляризованного слоя ЦТС с симметрией ∞m относительно оси поляризации. Влияние электрического поля на пьезоэлектрическую фазу может быть описано следующим образом:
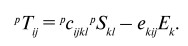. (42)
где Ek – электрическое поле; pTij, pSkl, ekij, и pcijkl – напряжение, деформация, пьезоэлектрический коэффициент и тензор жесткости для пьезоэлектрической фазы.
Если предположить, что электрическое поле направлено вдоль оси поляризации, т.е. E3 = E, E1 = E2 = 0, то получим:
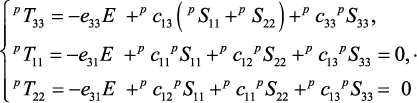(43)
Предположим, что ось поляризации пьезоэлектрической фазы совпадает с осью [111] магнитострикционной фазы. В этом случае получим выражение для магнитострикционной фазы:
(44)
где mTij и mSkl – тензоры напряжения и деформации магнитострикционной фазы.
Далее, следуя [24], мы рассмотрим структуру, состоящую из механически закрепленных магнитострикционных-пьезоэлектрических дисков без трения на границе раздела:
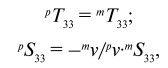(45)
где mv и pv – объемные доля магнитострикционной и пьезоэлектрической фаз, соответственно.
Решение (42), (44), (45) приводит к соотношению:
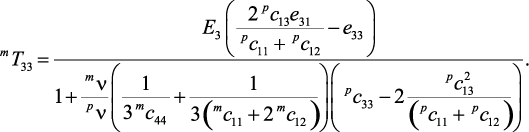(46)
Известно, что внешние механические напряжения приводят к сдвигу резонансного магнитного поля для ферритовой фазы [50]. Ограничимся случаем, когда магнитное и электрическое поля направлены вдоль оси поляризации пьезоэлектрического слоя в направлении [111] магнитострикционного слоя. Тогда можно получить:
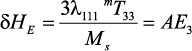(47)
где А – магнитоэлектрическая константа; Ms – намагниченность насыщения магнитострикционного слоя.
Отличительной особенностью резонансного МЭ эффекта является тот факт, что численное значение сдвига резонансного поля монотонно увеличивается от нулевого значения при увеличении объемной доли пьезоэлектрической фазы. Однако на низких частотах гигантский MЭ эффект наблюдается приблизительно для равных объемных долей компонент [11, 13]. Таким образом, можно сделать вывод, что объемная доля пьезоэлектрической фазы должна быть достаточно высокой, а также необходимо использовать пьезоэлектрический компонент с большим пьезоэлектрическим коэффициентом, а магнитострикционный компонент с малой намагниченностью насыщения и высокой магнитострикцией. При этом следует учитывать, что интенсивность линии магнитного резонанса будет ослабевать, если концентрация магнитострикционной фазы будет слишком низкой.
Таким образом, расчет резонансного МЭ эффекта для рассмотренной модели композита следует проводить в следующей последовательности:
1. Определить деформацию mS33 в зависимости от напряжения mT33.
2. Определить напряжение pT33 как функцию деформации pS33.
3. Определить напряжение mT33, используя граничные условия для границы раздела.
4. Определить сдвиг резонансной линии, используя известные соотношения для зависимости резонансного магнитного поля от механического напряжения.
Следовательно, задача сводится к решению уравнения упругих колебаний при определенных граничных условиях.
Для расчетов будем использовать следующие материальные параметры исходных компонентов:
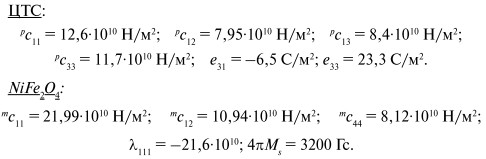
Согласно уравнениям (46) и (47) сдвиг резонансной линии в результате приложения электрического поля равен:
δH = A•E, при A » 2 Э•см/кВ,
где δH измеряется в Э, E – в кВ/см.
Для упрощения расчетов принято m v/p v = 1.
С точки зрения МЭ свойств, композиты в макроскопическом масштабе можно считать однородным материалом, т.е. МЭ композит можно рассматривать как реальный «материал» с МЭ эффектом, который отсутствует в исходных фазах [50]. В этом случае влияние внешнего постоянного электрического поля Е на спектр магнитного резонанса может быть описано с помощью дополнительного слагаемого в термодинамическом потенциале:
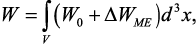(48)
где W0 – плотность термодинамического потенциала при Е = 0, а
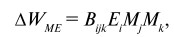, (49)
где Bijk – МЭ коэффициент. DWME может быть найдено с помощью
подхода, описанного в [20, 21], с учетом упругих, магнитоупругих,
магнитострикционных, пьезоэлектрических и электрострикционных свойств на
основании заданных граничных условий. В качестве практического примера
рассмотрим описанный выше случай, когда используется магнитострикционная
фаза с кубической симметрией, намагниченность которой лежит в плоскости
(110) и направлена под углом q относительно кубической оси [001]. Для
упрощения вычислений примем, что направление намагниченности совпадает
с одноосным напряжением mT33. Для M0//[111]
получим дополнительное слагаемое в плотности энергии в виде:
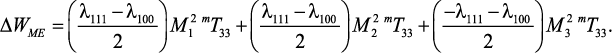(50)
Условие магнитного резонанса записывается в известной форме:
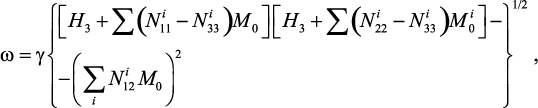(51)
где H3 – проекция внешнего магнитного поля на направление равновесной намагниченности M0;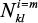 
– геометрические факторы размагничивания; 
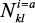– эффективные размагничивающие факторы магнитной кристаллической анизотропии; 
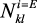– эффективные размагничивающие факторы вследствие МЭ взаимодействия.
Далее ограничимся рассмотрением одноосной структуры с симметрией 3m. В этом случае выражение (39) для плотности термодинамического потенциала может быть переписано в виде:
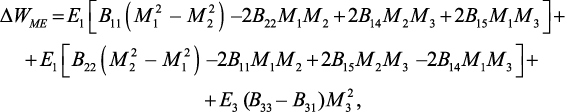(52)
где вводятся обычные двухиндексные обозначения: Bijk = Bil (l = 1,
2, 3, 4, 5, 6 соответствует j = 1 и k = 1, j = 2 и k = 2, j = 3
и k = 3, j = 2 и k = 3, j = 1 и k = 3, j = 1 и k = 2 соответственно);
bijk = blm (ij ⇔ l = 1...6,
kl ⇔ m = 1...6).
Согласно методу размагничивающих факторов эффективное магнитное поле вычисляется следующим образом:
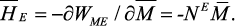(53)
Уравнение (53) должно быть записано в системе координат (1’, 2’,
3’), для которой ось 3’ совпадает с направлением равновесия
намагниченности M0. Компоненты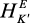 
задаются как:
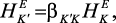(54)
где матрица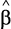 
может иметь вид
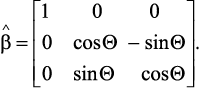(55)
Очевидно, что
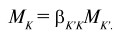. (56)
Подставляя (55) в (56) и принимая во внимание результаты
(47)–(48), получим:
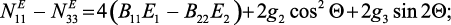
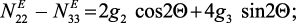(57)
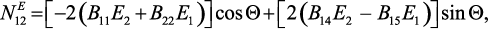
где g2 = –B11E1 + B22E2 + (B31 – B33)E3; g3 = –B14E1.
Следует отметить, что в выражении (29) опущены штрихи. Индексы в правой части уравнения (29) соответствуют кристаллографической системе координат. Далее рассмотрим случай, когда электрическое поле направлено вдоль оси симметрии структуры, т.е.:
Е1 = Е2 = 0, Е3 = E.
Таким образом, получим:
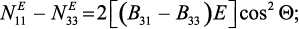
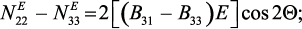(58)
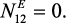
Для магнитострикционного слоя, расположенного в плоскости (111), при E//H// [111] с учетом кубической магнитной кристаллографической анизотропии и с учетом анизотропии формы [49, 50] получим выражение:
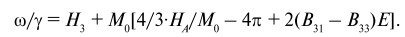(59)
Сдвиг резонансной линии в результате приложения электрического поля равен:
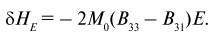(60)
Отметим, что в формуле (60) M0 – намагниченность слоистого композита как целого. Сравнение уравнения (60) с (47) дает
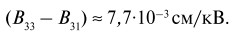(61)
Таким образом, МЭ константы могут быть найдены из экспериментальных данных по резонансному MЭ эффекту с помощью уравнения (60). Следовательно, можно описать поведение многослойных структур в приложенном электрическом поле и получить дополнительную информацию о характере MЭ взаимодействия. Для получения выражения для всех MЭ констант нужно провести анализ, аналогичный вышеприведенному, при соответствующей ориентации Е и Н.
Итак, уравнение (60) позволяет найти МЭ коэффициенты по данным измерений сдвига линии магнитного резонанса во внешнем электрическом поле. Описанный подход может быть использован для любого МЭ материала, который может быть монокристаллом или композитом. Кроме того, уравнения (46), (47) определяют внутреннюю структуру MЭ коэффициентов для композита, принимая во внимание, что MЭ эффект в феррит-пьезоэлектрической двухслойной структуре обусловлен механическими деформациями вследствие пьезоэлектрического и магнитострикционного взаимодействий.