Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Бичурин М И, Петров В М,
4.4. Магнитоэлектрическая восприимчивость феррит-пьезоэлектрического композита
Теперь рассмотрим композит, который подвергается воздействию
постоянных и переменных магнитного и электрического полей. Согласно
уравнению (2) необходимо рассмотреть взаимосвязь между переменной
намагниченностью и переменным электрическим полем для
нахождения тензора MЭ восприимчивости. Линеаризованное уравнение движения для намагниченности в данном случае может быть
записано в виде:
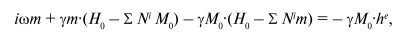(66)
где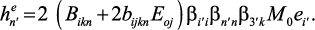 
Магнитная восприимчивость по отношению к эффективному магнитному полю he определяется формулой (30), т.е.:
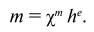(67)
На основании уравнения (30), принимая во внимание формулы (66) и (67), можно записать выражение для компонент MЭ восприимчивости [52]:
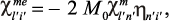(68)
где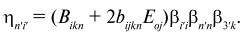 
Как видно из формулы (68), частотная зависимость магнитной и MЭ восприимчивости идентичны, а значение MЭ чувствительности определяется в основном MЭ константами и постоянным электрическим полем. Принимая во внимание внутреннюю структуру тензора магнитной восприимчивости, общее выражение для MЭ восприимчивости запишется в следующем виде:
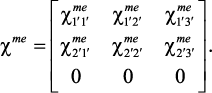(69)
Как видно из уравнения (69), третья строка тензора без учета магнитных потерь остается равной нулю. В отличие от тензора магнитной восприимчивости cme является асимметричным. Для практического использования полученных выражений рассмотрим тензор MЭ восприимчивости для групп симметрии 3 m и 4 mm. Все другие группы симметрии с одноосной структурой могут быть получены аналогично. Как следует из уравнения (67), тензор МЭ восприимчивости может быть получен путем умножения тензора магнитной восприимчивости из уравнения (30) на тензор η, определяемый формулой (68).
Примем, что направление равновесной намагниченности совпадает с осью симметрии структуры. В этом случае в уравнении (68) следует положить Q = 0 и Н0 = Н03. Для компонент тензора MЭ восприимчивости получим:
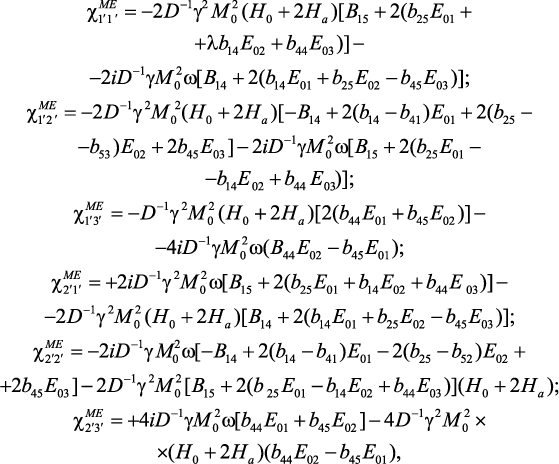(70)
где
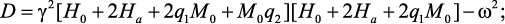
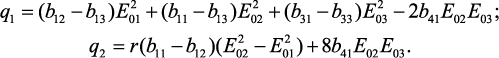
Рассмотрим образец в форме диска, вырезанный в базовой плоскости, во внешних электрическом и магнитном полях, направленных перпендикулярно плоскости диска (M0//E0//3). Тогда из уравнения (70) получаем:
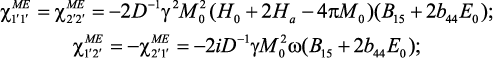(71)
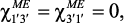
где
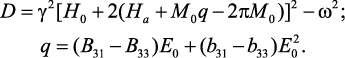
Из уравнения (71) видно, что в этом случае тензор МЭ
восприимчивости антисимметричен и может быть диагонализован. Для этой
цели мы используем циклические переменные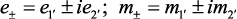 
Таким образом, мы получим:
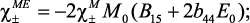(72)
где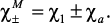 
Уравнение (72) позволяет получить оценку отношения магнитоэлектрической и магнитной восприимчивости. В качестве примера рассмотрим объемную композицию ЖИГ и ЦТС. Используя экспериментальные данные о линейном и билинейном МЭ эффекте [45] и принимая во внимание, что B15 ≈ B33 – B31, получим 2B15 M0 = 0,3 (Э•см)/кВ = 9•10–2 в гауссовых единицах. Пренебрегая квадратичным МЭ коэффициентом и подставляя значения B15 в формулу (72), получаем:
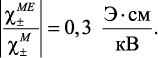
Если линейный МЭ коэффициент пренебрежимо мал, как это имеет место в случае неполяризованных образцов ЖИГ-ЦТС, а билинейная MЭ константа 4b44M0 = 0,7·10–2 Э•(см/кВ)2 и Е0 = 1 кВ•см, то можно найти:
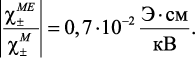
Для линейного и билинейного МЭ эффекта соотношение магнитных моментов mME/mM, индуцированных переменными электрическим и магнитным полями, прямо пропорционально отношению магнитоэлектрической и магнитной восприимчивости, приведенному выше. Предполагается, что моменты индуцированы одинаковой СВЧ мощностью.
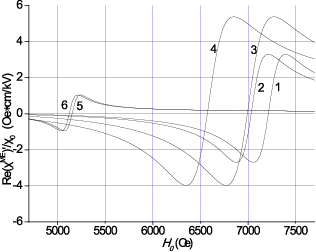
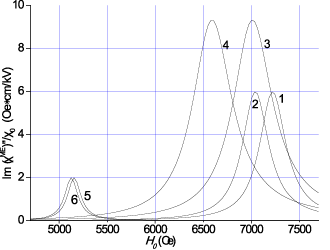
Зависимость МЭ восприимчивости от магнитного и электрического поля может быть получена из уравнения (72). В качестве примера рассмотрим двухслойные структуры ФЛ-ЦТС, ФН-ЦТС и ЖИГ-ЦТС. В отличие от [37], где была получена частотная зависимость MЭ восприимчивости во внутреннем поле для антиферромагнетика BaMnF4, на рис. 22 приведены расчетные зависимости действительной и мнимой частей MЭ восприимчивости в постоянном магнитном поле при наличии постоянного электрического поля. Результаты были получены, как и на рис. 17 и 18, для частоты 9,3 ГГц, при Е = 0 и 300 кВ/см.
Стоит отметить, что на рис. 22 представлено свойство МЭ композита, которое может быть определено как МЭ спектр композита. Значения резонансного поля, ширины и сдвига резонансной линии для двухслойной структуры такие же, как на рис. 17 и 18. Однако амплитуда резонансных линий определяется MЭ константами, как показано в уравнении (72). Поэтому мы получаем большую амплитуду для ФН-ЦТС, чем для ЖИГ-ЦТС.
а б
Рис. 22. Теоретическая зависимость действительной (а) и мнимой(б)
частей МЭ восприимчивости от подмагничивающего поля для двухслойных структур ФЛ-ЦТС (кривые 1 и 2), ФН– ЦТС (кривые 3 и 4)
и ЖИГ– ЦТС (кривые 5 и 6) для частоты 9.3 GHz. Кривые 1, 3 получены
при E = 0, кривые 2, 4 – для E = 300 kV/cm
Многослойные композиты ФЛ-ЦТС были приготовлены на основе пленок
толщиной 15 микрометров. Образцы, содержащие 16 чередующихся слоев ФЛ
и 15 слоев ЦТС, были изготовлены методом спекания при 1450 К.
Исследования ферромагнитного резонанса на частоте 9,3 ГГц проводили при
комнатной температуре на дискообразных образцах диаметром 4 мм
и толщиной 0,5 мм. Статическое магнитное поле было приложено
перпендикулярно плоскости образца, а поглощение мощности было измерено
как функция от H. Линия ФМР имела ширину 300 Э. Образцы были подвергнуты
воздействию постоянного электрического поля, перпендикулярного его
плоскости, при этом было получено резонансное поглощение при изменении
статического магнитного поля для ряда электрических полей. Рис. 23
показывает изменение сдвига резонансного магнитного поля dHE как функцию
от Е. Зависимость сдвига резонансного поля в электрическом поле
является линейной, что указывает на отсутствие
билинейных МЭ эффектов.
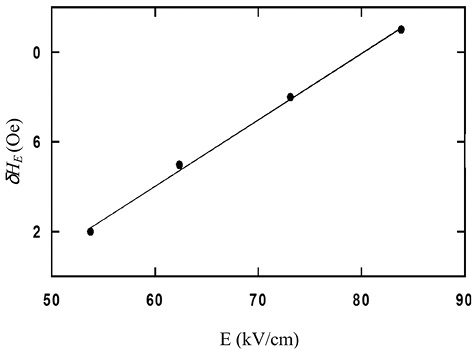
Рис. 23. Зависимость сдвига резонансного магнитного поля от постоянного электрического поля на частоте 9,3 ГГц для структуры ФЛ-ЦТС
По данным рис. 23 получаем для линейного MЭ коэффициента 2Mo(B31 – B33) = 0,4 (Э•см)/кВ. Из уравнения (72), получим отношение МЭ и магнитной восприимчивостей для многослойного композита состава ФЛ-ЦТС:
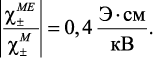
Используя теоретические данные, можно получить этот параметр для двухслойного композита равный 0,6 (Э•см)/кВ. Аналогичные данные, но для других комбинаций ориентации Е и Н, могут быть использованы для определения других МЭ констант.
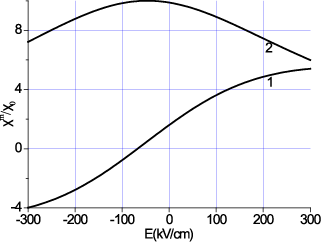
MЭ константы, полученные таким образом, могут быть использованы для расчета восприимчивости композита ФЛ-ЦТС. На рис. 24 показаны расчетные зависимости действительной и мнимой частей магнитной восприимчивости как функции H и E на частоте 9,3 ГГц. Другие параметры материала, используемого в расчете, следующие: H0 + 2Ha – 4pM0 = 3300 Э, a = 0,03. Эти оценки выполнены для образца в виде диска, намагниченного вдоль оси симметрии. Для того чтобы явно показать резонанс в электрическом поле, постоянное магнитное поле устанавливается равным полю ФМР. На рис. 25 показаны расчетные зависимости МЭ восприимчивости от постоянного магнитного поля при различных величинах постоянного электрического поля.
а б
Рис. 24. Зависимость магнитной восприимчивости от
подмагничивающего (а) и внешнего электрического (б) полей для слоистой
структуры ФЛ-ЦТС:
1 и 3 – Е = 0; 2 и 4 – Е = 300 kV/cm
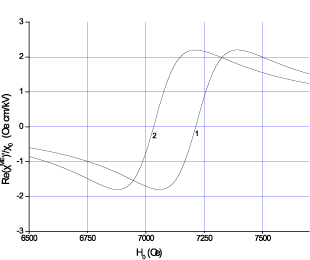
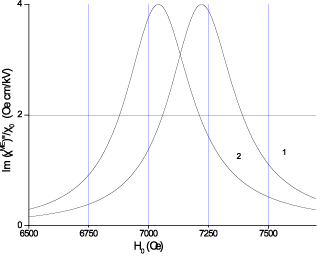
a б
Рис. 25. Зависимость действительной (а) и мнимой (б) частей МЭ восприимчивости от подмагничивающего поля для слоистой
структуры ФЛ-ЦТС: 1 – Е = 0; 2 – Е = 300 kV/cm
Как отмечалось выше, изменение внешнего постоянного электрического поля влияет в той же степени на магнитную и МЭ восприимчивости, как и изменение магнитного поля и обнаруживает резонансное поведение. Рис. 24 и 25 содержат важную информацию о высокочастотных магнитной и MЭ восприимчивостях для ФЛ-ЦТС композитов. Полученные результаты позволяют провести сравнение характеристик MЭ свойств многослойных и двухслойных композитов состава ФЛ-ЦТС, ФН-ЦТС и ЖИГ-ЦТС, приведенных на рис. 24–25. Влияние электрического поля на магнитную восприимчивость в ФЛ-ЦТС сильнее, чем в ЖИГ-ЦТС, но слабее по сравнению с ФН-ЦТС. Ширина E-резонанса острее, чем для ЖИГ-ЦТС. В целом, система ФЛ-ЦТС показывает сильный высокочастотный MЭ эффект и имеет большое значение для потенциального использования материала для электрически управляемых устройств СВЧ.
Следует подчеркнуть, что МЭ устройства, основанные на сдвиге резонансного магнитного поля во внешнем постоянном электрическом поле, представляют интерес для микроволновой области электромагнитного спектра. Сдвиг резонансного поля в таких материалах должен по крайней мере быть равным ширине резонансной линии [51]. Как видно из рис. 17, 18 и 21, все композиты, рассмотренные здесь, удовлетворяют ключевым требованиям, так как величина сдвига линии определяется внешним электрическим полем. Результаты на рис. 17 указывают на пригодность использования ФН-ЦТС композитов для устройств, таких как фазовращатели и аттенюаторы, поскольку сдвиг линии ФМР равен 450 Э в поле E = 300 кВ/см при ширине резонансной линии 450 Э. Результаты МЭ восприимчивости, представленные на рис. 24 и 25, свидетельствует о потенциальных возможностях применения композитов для других типов устройств, таких как устройства на связанных волнах, параметрические генераторы и трансформаторы. Ключевым параметром для таких устройств является коэффициент пропускания, определяемый поглощенной мощностью и амплитудой резонансной линии, которая максимальна для структуры ФН-ЦТС. Таким образом, приведенная теория позволяет определить MЭ характеристики композитов состава феррит-ЦТС в микроволновом диапазоне и возможности их практического применения.