
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.5.3. Влияние обменного взаимодействия на магнитоэлектрический эффект
Известно, что влияние обменного взаимодействия на магнитоупругие волны усиливается с частотой. В данном разделе анализируется влияние магнитного обменного взаимодействия на MЭ эффект в области МАР в феррит-пьезоэлектрических двухслойных наноструктурах [56–57].
Предполагается, что пьезоэлектрическая фаза толщиной L1
поляризована электрическим полем E0, приложенным вдоль направления х,
а микроволновое электрическое поле лежит в плоскости образца
и направлено вдоль z. Считается, что подмагничивающее поле Н0 приложено
вдоль z, а переменное магнитное поле h – вдоль оси у (в плоскости
двухслойной структуры). Сначала следует найти решение уравнения движения
намагниченности феррита и уравнения движения среды для
пьезоэлектрика и феррита. Система уравнений движения намагниченности и движения среды для ферритовой фазы имеет вид:
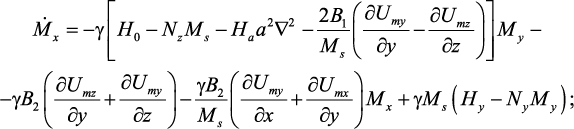
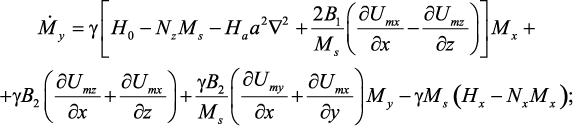 (86)
(86)
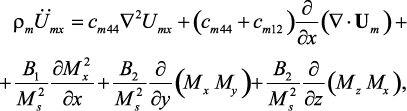
где Ha – обменное поле, a – постоянная решетки для ЖИГ. Затем мы приняли Mz = Ms и hx = 0, поскольку переменное магнитное поле приложено вдоль оси y. Кроме того, для данной ориентации композита имеем Nx = 4p, Ny = Nz = 0.
Решение уравнений движения намагниченности и движения среды позволяет найти смещение слоев и индуцированного напряжения в пьезоэлектрическом слое при условии разомкнутой цепи. Для MЭ коэффициента по напряжению получим следующее выражение:
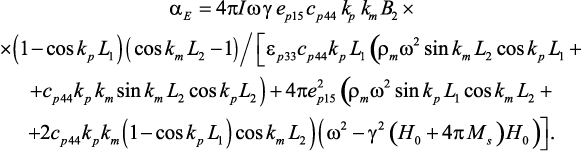 (87)
(87)
где L1 и L2 – толщины пьезоэлектрической и ферритовой фаз,
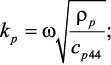
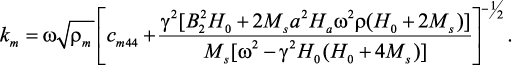
Разработанная в работе теория применяется к двухслойной структуре ЖИГ-ЦТС. Толщины слоев ЖИГ и ЦТС предполагаются равными 100 и 195 нм соответственно, чтобы толщинная мода имела такую же частоту, что и ФМР в ЖИГ. На рис. 30 показана частотная зависимость aE. Результаты приводятся для подмагничивающего поля H0 = 1140 Э при совпадении ФМР и фундаментальной моды ЭМР, а также для H0 = 2850 Э при совпадении ФМР и второй гармоники ЭMР. Рассмотрим результаты для подмагничивающего поля 1140 Э. Симметричная кривая с пиком aE, равном 65 В/см•Э, наблюдается, когда обменный параметр Ha = 0. Влияние обменного взаимодействия состоит в заострении резонансной кривой и увеличении пика aE на 30 % при уменьшении резонансной частоты. Мы получаем «обменное усиление» MЭ эффекта. Ожидается, что аналогичные эффекты будут наблюдаться на частоте 10 ГГц при увеличении подмагничивающего поля до 2850 Э. Если рассматривать влияние обменного взаимодействия, то на рис. 30 можно обнаружить увеличение пика aE на 60 % и широкий выступ на резонансной кривой вследствие возбуждений магнитоакустических мод.
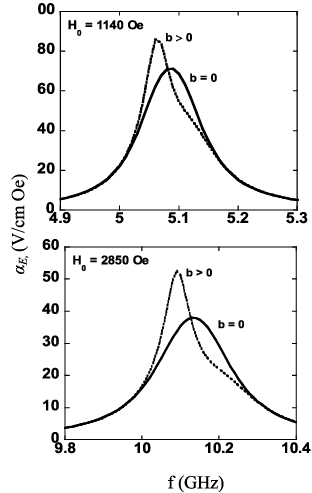
Рис. 30. Частотная зависимость aE для H0 = 1140 Э и H0 = 2850 Э с учетом
и без учета обменного взаимодействия
На рис. 31 показано влияние толщин ЦТС и ЖИГ на МЭ эффект. При отношении толщин 0,74 рис. 31 показывает уширенную резонансную кривую малой интенсивности. Если толщина ЦТС уменьшается так, что отношение становится равным 0,32, то можно заметить острый магнитоакустический резонанс. При дальнейшем уменьшении толщины ЦТС происходит снижение пика aE и смещение частот спин-акустических волн в сторону больших значений.
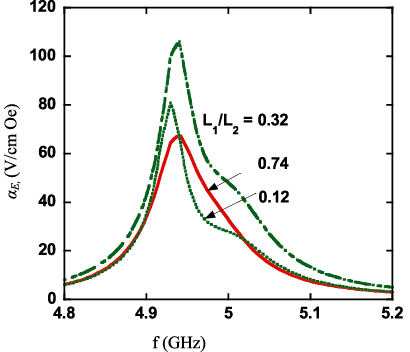
Рис. 31. Влияние толщин ЦТС и ЖИГ на МЭ эффект
Зависимости максимального значения aE от отношения толщин пьезоэлектрического и магнитного слоев приведены на рис. 32. Для малых толщин ЦТС aE остается малым и увеличивается при увеличении толщины. Поскольку ЭМР в ЦТС способствует максимальной передаче высокочастотной энергии в магнитную систему, ожидается увеличение aE с ростом толщины ЦТС. Но для отношения толщин равного 0,32, наблюдается падение МЭ коэффициента. Таким образом, максимум МЭ эффекта ожидается, когда толщина слоя ЖИГ в три раза больше по сравнению с ЦТС.
Обсуждаемая теория и оценки для двухслойных структур ЖИГ-ЦТС могут быть использованы при проведении экспериментов по магнитно-акустическому резонансу и изучению влияния магнитного обменного взаимодействия. MЭ взаимодействие в таких двухслойных структурах может быть использовано для создания таких устройств, как резонаторы или фазовращатели на основе магнитоакустических волн.

Рис. 32. Зависимость максимального значения aE от отношения толщин пьезоэлектрического и магнитного слоев L1/L2 для H0 = 1100 Oe
