
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.2. Математическое моделирование процессов массопереноса при синтезе УВНМ
Рассмотрим элемент реакционной зоны, включающий в себя движущийся
вдоль оси x, в ламинарном режиме, со скоростью ω (ω = ωx) газовый поток
и подложку с распределенным на ней катализатором (см. рис. 3.2). Система
находится в стационарном
режиме.
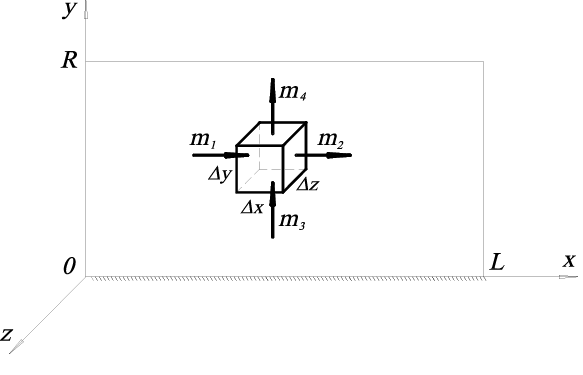
Рис. 3.2. Элемент реакционной зоны (к выводу дифференциального уравнения массопереноса)
В элементе реакционной зоны выделим бесконечно малый объем размеров Δx, Δy, Δz (рис. 4.2). Составим материальный баланс для бесконечно малого объема, рассматриваемого в момент времени Δτ:
m1 – m2 + m3 – m4 = 0. (3.3)
Входящие в уравнение (3.3) компоненты есть массы вещества, поступающие и покидающие элементарный объем за счет явления конвективного массопереноса (m1, m2) и молекулярной диффузии (m3, m4):
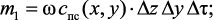 (3.4)
(3.4)
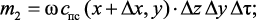 (3.5)
(3.5)
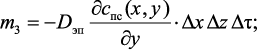 (3.6)
(3.6)
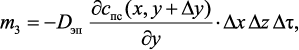 (3.7)
(3.7)
где x, y – пространственные координаты; ω – линейная скорость газового потока; cпс(x, y) – стационарное поле концентрации химически связанного углерода в газовом потоке; Dэп – коэффициент эффективной молекулярной диффузии углеводорода газовом потоке.
Подставив выражения (3.4)–(3.7) в уравнение (3.3) получим
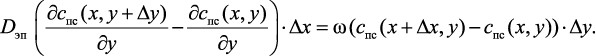 (3.8)
(3.8)
Поделим левую и правую часть уравнения (3.8) на ΔxΔy и выполнив предельный переход, получаем дифференциальное уравнение стационарного массопереноса к слою катализатора от газового потока, движущегося в ламинарном режиме:
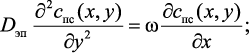
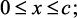
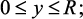 (3.9)
(3.9)
условия однозначности:
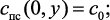 (3.10)
(3.10)
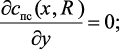 (3.11)
(3.11)
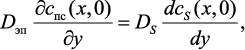 (3.12)
(3.12)
где с – длина подложки с нанесенным на нее катализатором; R – высота над подложкой с катализатором; с0 – начальная концентрация химически связанного углерода в потоке на входе в реакционную зону; DS – коэффициент эффективной диффузии углерода в частице катализатора.
Решения задачи (3.9)–(3.12) выполняем метод конечных интегральных преобразований [240].
С цель упрощения записи решения сделаем замену:
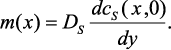 (3.13)
(3.13)
Для исключения координаты y используем интегральное преобразование вида:
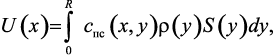 (3.14)
(3.14)
причем весовая функция r(y) = 1, а ядро интегрального преобразования S(y) является решением вспомогательной задачи с однородными граничными условиями:
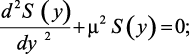 (3.15)
(3.15)
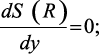 (3.16)
(3.16)
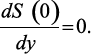 (3.17)
(3.17)
Решение ищется с точностью до постоянного множителя в виде [241]:
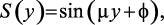 (3.18)
(3.18)
причем числа μ и φ определяются из граничных условий (3.16), (3.17):
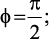 (3.19)
(3.19)
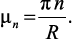 (3.20)
(3.20)
Тогда
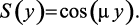 (3.21)
(3.21)
Обратный переход выполняется по формальной формуле:
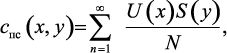 (3.22)
(3.22)
где
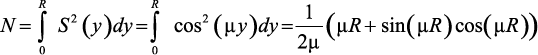 . (3.23)
. (3.23)
Суммирование в (3.22) ведется по значениям mn.
Переходим к изображениям задачи (3.9)–(3.12).
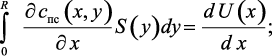 (3.24)
(3.24)
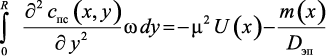 , (3.25)
, (3.25)
тогда
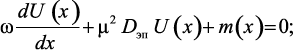 (3.26)
(3.26)
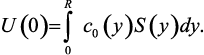 (3.27)
(3.27)
Решением задачи (3.26)–(3.27) является функция [241]:
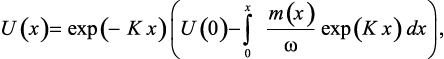 (3.28)
(3.28)
где
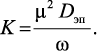 (3.29)
(3.29)
Коэффициент эффективной диффузии углерода в частице катализатора DS есть количественная мера активности катализатора.
Использования полученного решения в практических расчетах требует информации о значениях коэффициентов эффективной диффузии: углерода в потоке (Dэп) (как химически связанного в виде углеводородов); атомарного углерода в объеме каталитической частицы (DS). На практике, не представляется возможным оценить аддитивный вклад каждого коэффициента эффективной диффузии в процесс массопереноса, поэтому для практических расчетов целесообразно исключить из рассмотрения градиент концентрации, перпендикулярный газовому потоку (вдоль координаты y), а коэффициент эффективной диффузии заменить коэффициентом массоотдачи, определяемым экспериментальным путем.
Выделим элементарную область длиной Δх по направлению движения потока (рис. 3.3).
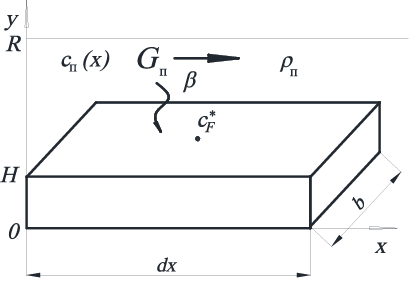
Рис. 3.3. Эскиз элементарной области для задачи стационарного переноса массы газовым потоком
Масса углеводных радикалов, привносимая потоком газа за время Δτ:
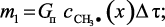 (3.30)
(3.30)
масса углеводородных радикалов, уносимая потоком газа за время Δτ
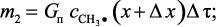 (3.31)
(3.31)
масса углеводородных радикалов, отдаваемая элементарной области поверхностью
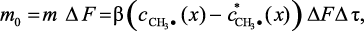 (3.32)
(3.32)
где 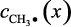 –
поле концентрации углеводородных радикалов в потоке; Gп – массовый
расход газа; m – удельный массовый поток через поверхность катализатора;
ΔF – площадь поверхности катализатора в элементарной области; β –
коэффициент массоотдачи от потока к поверхности катализатора;
–
поле концентрации углеводородных радикалов в потоке; Gп – массовый
расход газа; m – удельный массовый поток через поверхность катализатора;
ΔF – площадь поверхности катализатора в элементарной области; β –
коэффициент массоотдачи от потока к поверхности катализатора; 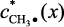 – равновесная концентрация на поверхности катализатора;
– равновесная концентрация на поверхности катализатора;
Площадь поверхности катализатора в элементарной области находится из следующего соотношения:
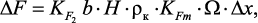 (3.33)
(3.33)
где 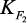 –
удельная поверхность катализатора, м2кг–1; b – ширина подложки
с катализатором; H – высота слоя катализатора; ρк – насыпная плотность
катализатора; KFm – коэффициент активности поверхности катализатора; Ω –
доля восстановленной поверхности катализатора.
–
удельная поверхность катализатора, м2кг–1; b – ширина подложки
с катализатором; H – высота слоя катализатора; ρк – насыпная плотность
катализатора; KFm – коэффициент активности поверхности катализатора; Ω –
доля восстановленной поверхности катализатора.
Составляющие элементарного материального баланса можно записать через приращения независимых переменных:
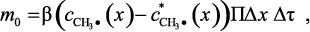 (3.34)
(3.34)
где 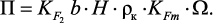
Материальный баланс элементарной области в стационарном режиме:
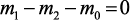 (3.35)
(3.35)
или
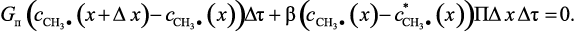 (3.36)
(3.36)
Разделив левую и правую часть уравнения на произведение ΔхΔτ, и выполнив предельный переход, получим:
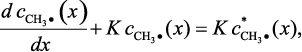 (3.37)
(3.37)
где 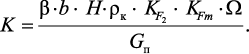
При начальном условии 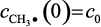 уравнение (3.37) имеет решение [241]:
уравнение (3.37) имеет решение [241]:
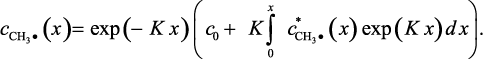 (3.38)
(3.38)
