Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.3. Математическое моделирование процессов теплопереноса при синтезе УВНМ
Рассмотрим элемент реакционной зоны, включающий в себя движущийся вдоль оси x с массовым расходом (Gп) газовый поток и подложку с распределенным на ней катализатором находящийся в стационарном теплообменном режиме.
Выделим элементарную область длиной Δх по направлению движения потока (рис. 3.4).
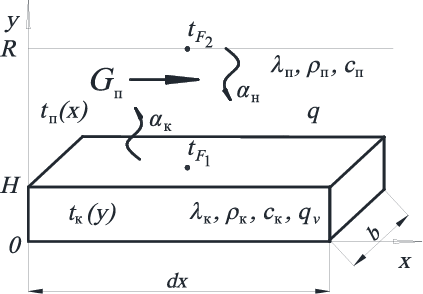
Рис. 3.4. Эскиз элементарной области для задачи
стационарного теплопереноса
Тепловой баланс элементарной области в стационарном режиме
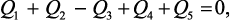(3.39)
где тепло, привносимое потоком газа за время Δτ:
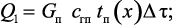(3.40)
тепло, отдаваемое элементарной области поверхностью раздела фаз (газовый поток – катализатор):
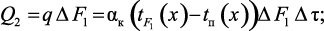(3.41)
тепло, уносимое потоком газа за время Δτ
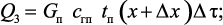(3.42)
тепло, отдаваемое элементарной области поверхностью раздела фаз (газовый поток – обогревающая поверхность):
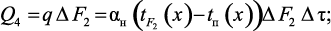(3.43)
тепловой эффект объемных гомогенных химических реакций за время Δτ:
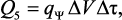(3.44)
где tп(x) – текущая температура газового потока; сгп – теплоемкость газового потока; q – плотность теплового потока через границу раздела фаз; ΔF1 – площадь поверхности теплообмена со слоем катализатора и УВНМ; ΔF2 – площадь поверхности теплообмена с обогревающей поверхностью; αк – коэффициент конвективной теплоотдачи от слоя катализатора и УВНМ к газовому потоку; αн – коэффициент конвективной теплоотдачи от обогревающей поверхности к газовому потоку; tF1(x) – температура поверхности катализатора; tF2(x) – температура обогревающей поверхности; qψ – распределенный тепловой эффект объемной гомогенной химической реакции, Вт/м3.
Площади раздела фаз в элементарной области, образованная поверхностями частиц катализатора и образующегося углеродного наноматериала и обогревающей поверхности находится из следующего соотношения:
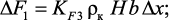(3.45)
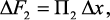(3.46)
где H – средняя высота слоя твердой фазы; b – средняя ширина слоя твердой фазы; ρк – насыпная плотность твердой фазы; KF1 – удельная поверхность твердой фазы, м2·кг–1; П2 – периметр обогревающей поверхности.
Составляющие элементарного теплового баланса (3.41), (3.43) и (3.44) можно записать через приращения независимых переменных:
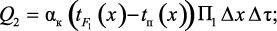(3.47)
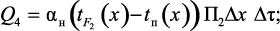(3.48)
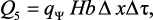(3.49)
где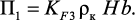 
Поставив выражения (3.40), (3.42), и (3.47)–(3.49) в уравнение (3.39):
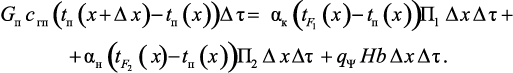(3.50)
Разделив левую и правую часть уравнения (3.50) на произведение ΔхΔτ и выполнив предельный переход, получаем:
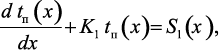(3.51)
где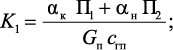 
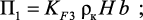
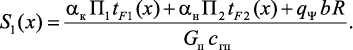
При начальном условии вида tп(0) = t0 уравнение (3.51) имеет решение [241]:
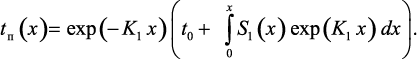(3.52)
При условии, tF1(x) = const = tF1 и tF2(x) = const = tF2 решение уравнения (3.51) имеет вид:
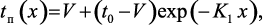(3.53)
где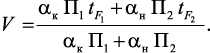 
Средняя температура газового потока на участке длиной Δх:
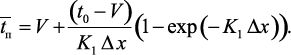(3.54)
Значение температуры поверхности раздела фаз для условия tF1(x) = const = tF является решением стационарной задачи теплопроводности слоя твердой фазы:
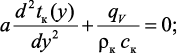
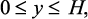(3.55)
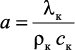– температуропроводность твердой фазы;
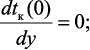(3.56)
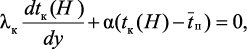(3.57)
где tк(y) – поле температуры в твердой фазе; qV – распределенный источник мощности тепловыделения (тепловой эффект дегидрирования углеводородных радикалов, формирования УВНМ и выделение тепла при использование радиационных методов нагрева слоя катализатора), Вт/м3; λк – теплопроводность твердой фазы; cк – теплоемкость твердой фазы.
Решение уравнения (3.55) с учетом граничных условий (3.56)–(3.57) имеет вид:
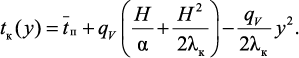(3.58)
Средняя температура слоя твердой фазы толщиной H:
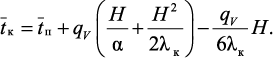(3.59)