Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.5. Математическое моделирование процесса восстановления катализатора при синтезе УВНМ
В соответствии с макрокинетическим подходом синтеза УВНМ, рассмотренном во второй главе, процесс восстановления катализатора лимитируется стадией внешней массоотдачи.
Выделим элементарную область длиной Δх по направлению движения газового потока.
Масса атомарного водорода, привносимая потоком газа за время Δτ:
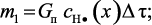(3.96)
масса атомарного водорода, уносимая потоком газа за время Δτ
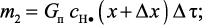(3.97)
масса атомарного водорода, отдаваемая из элементарной области поверхности
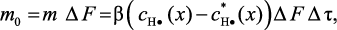(3.98)
где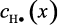 
–
поле концентрации атомарного водорода в потоке; Gп – массовый расход
газа; m – удельный массовый поток через поверхность катализатора; ΔF –
площадь поверхности не восстановленного катализатора в элементарной
области; β – коэффициент массоотдачи от потока к поверхности
катализатора; 
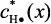– равновесная концентрация на поверхности катализатора;
Площадь поверхности не восстановленного катализатора в элементарной области находится из следующего соотношения:
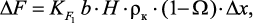(3.99)
где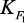 
–
удельная поверхность катализатора, м2кг–1; b – ширина подложки
с катализатором; H – высота слоя катализатора; ρк – насыпная плотность
катализатора; Ω – доля восстановленной поверхности катализатора.
Составляющие элементарного материального баланса можно записать через приращения независимых переменных:
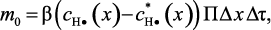(3.100)
где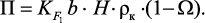 
Материальный баланс элементарной области в стационарном режиме:
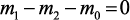(3.101)
или
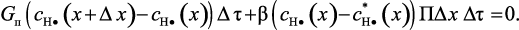(3.102)
Поделив левую и правую часть уравнения на произведение ΔxΔτ, и выполнив предельный переход, получим:
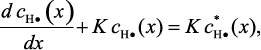(3.103)
где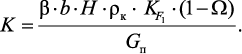 
При начальном условии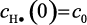 
уравнение (3.103) имеет решение [241]:
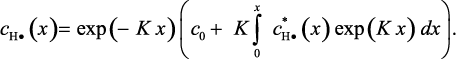(3.104)
Таким образом, изменение доли восстановленного катализатора за время прохождения газовым потоком отрезка Δх будет пропорциональна количеству атомарного водорода транспортированного к его поверхности:
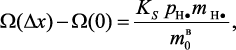(3.105)
где KS – стехиометрический коэффициент, определяющий количество
необходимого количества атомарного водорода для восстановления единицы
массы конкретного катализатора;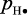 
– стерический фактор; 
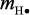– масса атомарного водорода транспортированного к поверхности катализатора; 
–
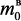начальная масса катализатора в перерасчете на восстановленное состояние
(без учета массы кислорода в оксиде активного компонента).
Масса атомарного водорода транспортированного к поверхности катализатора может быть выражена через изменение его концентрации в потоке в следствии массоотдачи к катализатору:
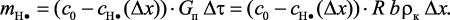(3.106)
Подставив уравнение (3.106) в (3.105), поделив левую и праву часть на Δx и сделав предельный переход, получим:
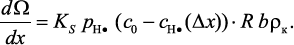(3.107)
Подставив уравнение (3.104) в (3.107) и выполнив упрощение, получим:
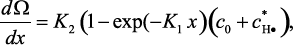(3.108)
где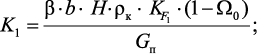 
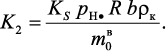
При начальном условии Ω(0) = Ω0 уравнение (3.108) имеет решение:
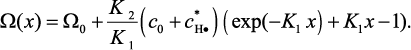(3.109)