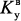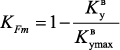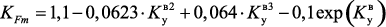Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Процессы и реакционное оборудование производства углеродных наноматериалов

Рухов А В,

4.4.1. Реализация математической модели переноса массы и энергии при синтезе УВНМ

Современная методика расчета основного реакционного оборудования синтеза углеродных наноструктур может быть реализована на основе математического моделирования квазистационарных полей определяющих параметров процесса (концентрации, температуры и др.). Данная методика может быть использована, как для выполнения технологических расчетов [например, определение времени цикла (для варианта периодической реализации процесса) при заданных конструктивных и режимных параметрах], так и для решения локальной задачи оптимизации (например, определение конструктивных и режимных параметров необходимых для обеспечения максимальной производительности или минимальной себестоимости продукта).

Концентрационные и температурные поля аппарата представляются в виде концентрационных и температурных полей локальных областей, моделируемых взаимосвязанными решениями задач тепло- и массопереноса, а их параметры являются функциями текущих концентраций и температур, расчет концентрационных и температурных полей каждой последующей локальной области выполняется по итеративной методике, предусматривающей многократное последовательное решение всех этих задач с текущим уточнением кинетических, физических и физико-химических характеристик рассматриваемых процессов. Локальная область включает в себя реакционный объем и конструктивные элементы аппарата. Такой подход позволяет при рациональном выборе размера локальной области с минимальным значением погрешности привести дифференциальные уравнения, описывающие данные процессы к линейной форме с целью получения их аналитических решений.

Блок-схема алгоритма расчета концентрационного и температурных полей в объеме основного оборудования синтеза УВНМ представлена на рис. 4.4.

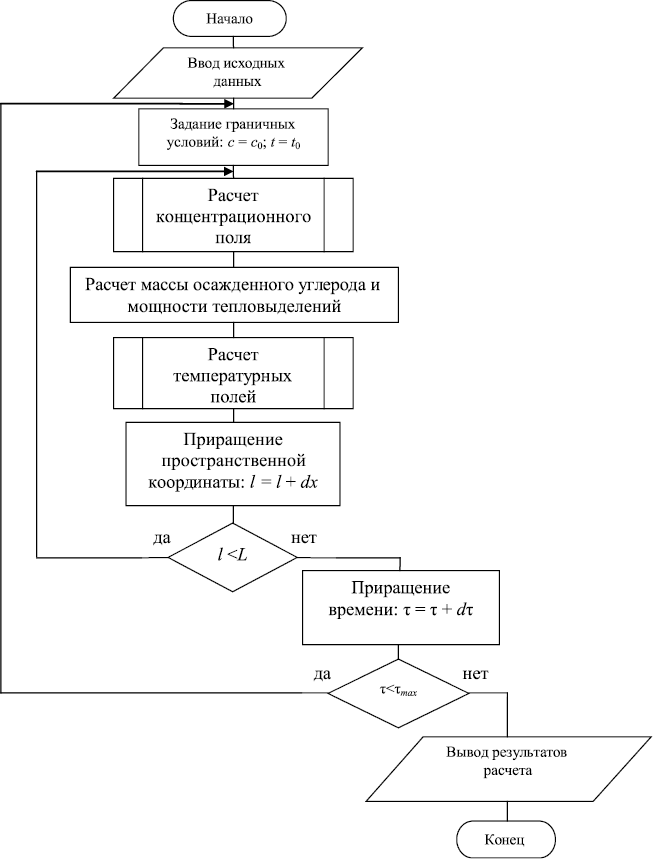
Рис. 4.4. Блок-схема алгоритма расчета концентрационного
и температурных полей в объеме основного
оборудования синтеза УВНМ

Для учета нестационарности величины активной поверхности катализатора, являющейся параметром рассматриваемого процесса в расчетный алгоритм вводится дискретизация по времени.

Развитие вычислительной техники наряду с использованием аналитических решений уравнений математической модели позволяет создать быстродействующие расчетные алгоритмы.

При последовательном расчете концентрационных и температурных полей локальной области начальная концентрация и температура каждой последующей области является конечной концентрацией и температурой предыдущей при фиксированном времени. А начальная масса структурированного углерода в виде твердой фазы являются массой углерода, осажденного за предыдущий период временной дискретизации dτ. Значения массы осажденного углерода используются для расчета коэффициента активности поверхности катализатора.

Методика расчета реализован на алгоритмическом языке программирования FreePascal (Copyright © 1998–2005 by BBrczi Gabor, Pierre Mullerand Peter Vreman) и представляет собой законченный программный продукт.

Основой алгоритма являются два вложенных цикла: один по времени с шагом dτ равным выбранному времени дискретизации, и второй цикл по длине подложки с дискретностью, равной длине локальной области dx.

Рассмотрим работу алгоритма. По значению начальной концентрации углеводорода и температуре потока с учетом явления взаимного растворения газов вычисляется скорость потока:

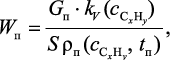(4.16)

где G – массовый расход газовой смеси; S – площадь сечения реакционной зоны; kV – коэффициент взаимного растворения компонентов газовой смеси, (отношение объема газовой смеси к сумме отдельно взятых объемов ее компонентов), при заданной концентрациях, ρп – плотность газового потока.

Из анализа экспериментальных данных исследования кинетики процесса получения УВНМ, представленных в пятой главе, известно, что скорость процесса со временем уменьшается пропорционально удельной массе осаженного на его поверхности углерода. Используя массу уже структурированного углерода рассчитывается значение активности поверхности катализатора:

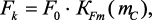(4.17)

где F0 – начальная поверхность катализатора (τ = 0); КFm – коэффициент активности поверхности катализатора.

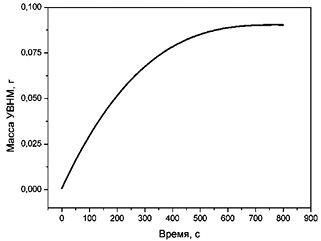
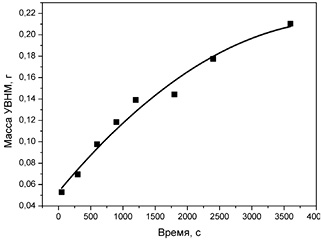
Численное значение коэффициента активной поверхности катализатора может быть получено при обработке экспериментальной зависимости массы синтезированного УВНМ от времени представленные на рис. 4.5:

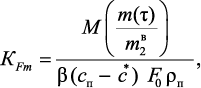(4.18)

где M –массовый расход извлекаемого углеводорода из потока, кг·с–1;
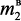 – масса восстановленного катализатора, кг; β – коэффициент массоотдачи от газового потока к поверхности катализатора, м·с–1); сп – концентрация углеводорода в потоке, кг/кгсм; с* – равновесная концентрация углеводорода на поверхности катализатора, кг/кгсм; F0 –активная поверхность катализатора в начале процесса; ρп – плотность газового потока, кг/м3.

Из источника [222] известно, что в одном грамме катализатора содержится порядка 1,8·1015 каталитических центров. Приняв допущение, что каталитические центры имеют сферическую форму со средний радиусом порядка 2·10–8 м (для катализатора NiO–MgO [258]) удельную поверхность катализатора можно рассчитать как произведение количества активных центров на половину их поверхности (вторая половина занята формирующейся наноструктурой):

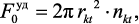(4.19)

где rkt – радиус каталитического центра, м; nkt = 1,8·1015– количество активных центров в одном грамме катализатора.

а б

а б

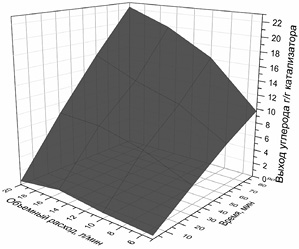
Рис. 4.5. Кинетика процесса синтеза УВНМ.
Углеродсодержащие вещество/катализатор/температура:
а – пропан-бутановая смесь/NiO–MgO/700 °С;
б – этанол/NiO–MgO/700 °С;
в – пропан-бутановая смесь/NiO–MgO/630 °С;
г – пропан- бутановая смесь/NiO–MgO/660 °С

Активная поверхность катализатора в начале процесса тогда рассчитывается:

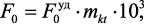(4.20)

где mkt – масса катализатора, г.

Массовый поток к поверхности катализатора (рис. 4.6) определяется как первая производная изменения массы во времени для зависимости представленной на рис. 4.5 а).

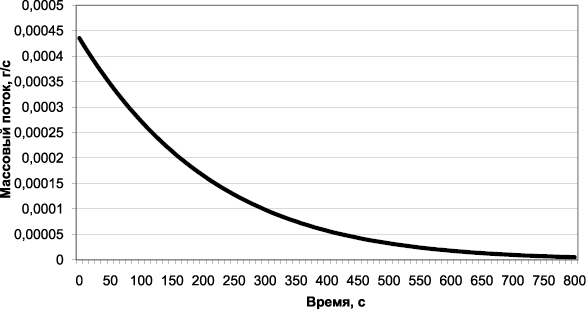
Рис. 4.6. Массовый поток углеводорода через поверхность катализатора

Обработка экспериментальных данных позволяет рассчитать максимальное и среднее значение коэффициента массоотдачи.

Максимальное значение коэффициента массоотдачи определяется:

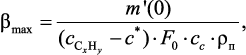(4.21)

где m′(0)– массовый поток в момент времени τ = 0, кг·с–1; сс – массовая доля углерода в углеводороде.

Среднее значение коэффициента массоотдачи определяется как:

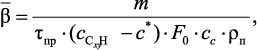(4.22)

где m – масса полученного УВНМ за время τпр, кг; τпр – время процесса синтеза, с.

При расчете коэффициента активности поверхности катализатора используется максимальное значение коэффициента массоотдачи, т.е. считается, что β = βmax = const, а уменьшение массового потока происходит за счет уменьшения поверхности контакта.

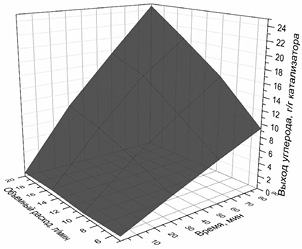
Зависимость значения коэффициента активности поверхности катализатора от удельного выхода наноструктурированного углерода по катализатору при пиролизе пропан- бутановой смеси и этанола представлена на рис. 4.7, катализатор NiO–MgO.

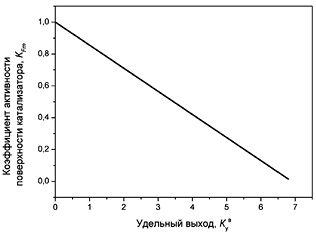
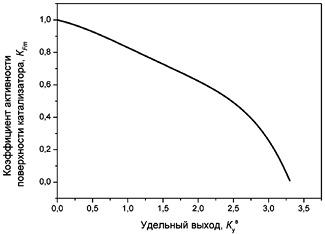
а б

Рис. 4.7. Зависимость коэффициента активности поверхности катализатора NiO-MgO от удельного выхода углерода по катализатору, при пиролизе:
а – пропан- бутановой смеси; б – этанола

Значения коэффициентов эффективной массоотдачи и зависимость активности поверхности катализатора от удельного выхода для процессов получения УВНМ на катализаторе NiO–MgO при пиролизе пропан- бутановой смеси и этанола представлены в табл. 4.1.

Таблица 4.1

Значения кинетических коэффициентов процесса получения УВНМ

где 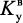,  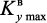– текущее и максимальное значение удельного выхода наноуглерода по катализатору, соответственно.

Далее рассчитывается поле концентрации и вычисляется концентрация углеводорода на границе элементарной области (на выходе из нее), а по разности начальной и конечной концентраций определяется масса углеводорода разложившегося на поверхности катализатора в элементарной области за время dτ. По значению расхода углеводорода, покинувшего поток, рассчитывается мощность теплового эффекта химической реакции пиролиза. Значение мощности теплового эффекта определяет значение удельной тепловой мощности, подводимой к веществу, расположенному на подложке в реакционной зоне:

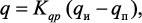(4.23)

где qи – удельная тепловая мощность, подводимая к реакционному объему, Вт/м3; qп – мощность теплового эффект, пиролиза углеводорода, отнесенная к объему твердого вещества, Вт/м3; Kqp – коэффициент мощности.

Удельная тепловая мощность, подводимая к реакционной зоне, определяется с использованием принципа суперпозиции:

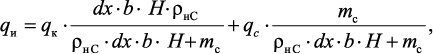(4.24)

где qи и qc – удельная тепловая мощность, подводимая к катализатору и полученному наноуглероду, соответственно, Вт/м3; dx – длина элементарной области, м; b – ширина подложки с катализатором, м; H – высота слоя катализатора; ρнС – насыпная плотность УВНМ.

Удельная тепловая мощность, расходуемая на процесс пиролиза:

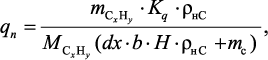(4.25)

где 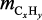 – расход углеводорода, подвергшегося пиролизу, кг·с–1; Kq – тепловой эффект реакции пиролиза, Дж/моль;  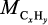– молекулярная масса углеводорода, кг/моль.

Для обеспечения постоянства качественных параметров наноструктур синтез реализуют при постоянной температуре катализатора, что исключает влияние факторов, вызванных неизотермичностью процесса. Такой режим работы реакционного оборудования обеспечивается реализацией автоматической системы регулирования температуры с принципом управления «по отклонению». Учет реальных условий проведения процесса в расчетной методике осуществляется введением коэффициента мощности (Kqp) являющимся решением нелинейного уравнения:

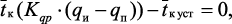(4.26)

где 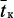, 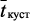– текущая и установленнаясредняя температура катализатора, соответственно, °С.

Решение уравнения (4.26) получено методом дихотомии [257]. Значение коэффициента мощности и динамика его изменения может быть использована при проектировании систем автоматического регулирования температуры катализатора.

Следующим этапом рассчитывается коэффициент теплоотдачи от газового потока к поверхности твердого вещества, расположенного на подложке.

В неподвижном слое зернистого материала коэффициент теплоотдачи между потоком и поверхностью частицы [259] можно определить из выражения:

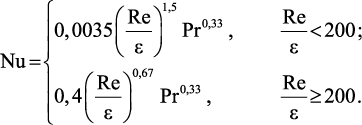(4.27)

Здесь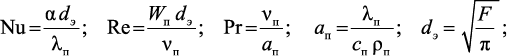  

Wп – скорость газового потока; F – площадь поверхности теплообмена; e – порозность зернистого слоя; λп, сп, ρп, νп – соответственно теплопроводность, теплоемкость, плотность и кинематическая вязкость газового потока при текущей температуре и концентрации углеводорода.

Коэффициент теплоотдачи излучением от частиц газу [239]:

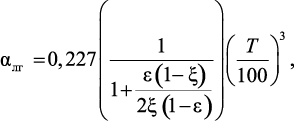(4.28)

где ξ – степень черноты поверхности частицы; T – абсолютная температура поверхности частиц.

Коэффициент теплоотдачи излучением между частицами [239]:

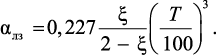(4.29)

Далее рассчитываются температурные поля поверхности теплообмена и газового потока в итеративном режиме с уточнением значения коэффициента теплоотдачи.

После уточнения концентрационного поля потока рассчитывается масса углерода, осажденного в виде наноструктуры за временя дискретизации. Значение массы наноуглерода сохраняется для использования в качестве начального условия в следующий момент времени.

Расчет последовательно проводится для всех локальных областей во временном интервале от 0 до 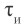с дискретизацией .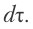