Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Архитектура и схемотехника управляемых усилителей и смесителей сигналов

Прокопенко Н Н, Будяков П С,

Глава 14. АРХИТЕКТУРЫ АНАЛОГОВЫХ КВАДРАТОРОВ НА ОСНОВЕ ДИФФЕРЕНЦИАЛЬНЫХ КАСКАДОВ С НЕЛИНЕЙНОЙ КОРРЕКЦИЕЙ

Анализ свойств дифференциальных каскадов (ДК) с нелинейной коррекцией проходной характеристики (ПХ) показывает, что при исключении линеаризующих ПХ резисторов на их основе возможен синтез аналоговых квадраторов (АК) напряжения. Данная концепция построения АК, несколько отличающаяся от ранее рассмотренной [67], позволяет реализовать широкую гамму АК с набором различных свойств по усилению, энергопотреблению, подавлению нежелательных спектральных составляющих, требованиями к симметрии входных сигналов и входным фазорасщепителям.

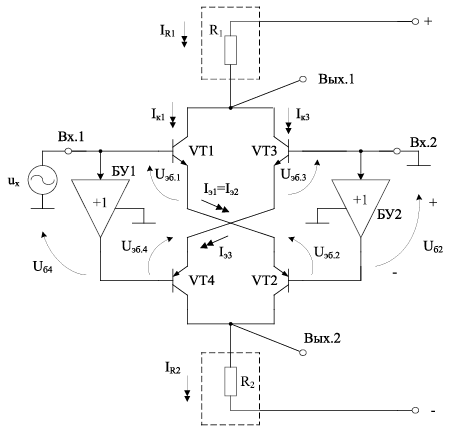
Базовая архитектура квадраторов предлагаемого подкласса приведена на рис. 14.1.

На основании второго закона Кирхгофа при ux = 0 можно записать следующие уравнения для входных цепей АК рис. 14.1a:

U_б4 = U _эб.4 + U _эб.3; (14.1)

U_б2 = U _эб.2 + U _эб.1, (14.2)

где Uб4, Uб2 – статические напряжения на базах транзисторов VT4 и VT2; Uэб.i – напряжение эмиттер-база i-го транзистора.

В статическом режиме (ux = 0) при идентичных p-n переходах транзисторов за счет схемотехники повторителей напряжения БУ1 и БУ2 обеспечивается равенство

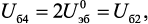(14.3)

где 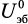 – напряжение эмиттер-база транзисторов при Iэ = Iэ.р, Iэ.р – статический ток эмиттера транзисторов.

При произвольном токе эмиттера Iэi = Iэ.р напряжение на эмиттерном переходе i-го транзистора отличается от 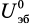в статистическом режиме:

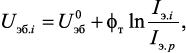(14.4)

где φт ≈ 26 мВ – температурный потенциал.

 

а

 

б

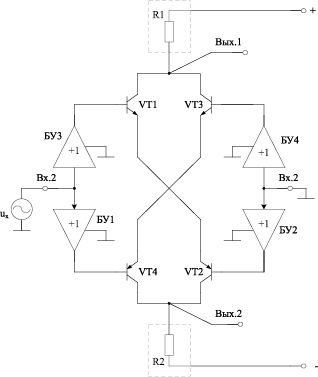
Рис. 14.1. Функциональные схемы аналоговых квадраторов на базе ДК с нелинейной коррекцией при несимметричном (а) и симметричном (б) управлении транзисторами VT1-VT4

Если на вход Вх.1 подается небольшое напряжение ux < φт, то из уравнений (14.1), (14.2), (14.3), (14.4) можно получить следующие зависимости

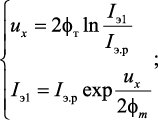(14.5)

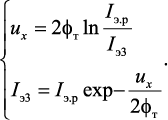(14.6)

Таким образом, при ux > 0 ток коллектора транзистора VT1 возрастает по экспоненте, а ток коллектора транзистора VT5 уменьшается по экспоненте относительно статического значения Iэ.р. В результате ток в цепи нагрузки R1 является суммой двух экспонент:

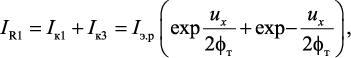(14.7)

где Iк1 – коллекторный ток транзистора VT1; Iк3 – коллекторный ток транзистора VT3.

Функцию (3.7) можно представить в виде нормированной зависимости:

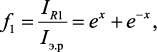(14.8)

где 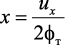 – относительный переменный параметр.

Сумма двух экспонент ex и e–x может быть представлена в виде ряда

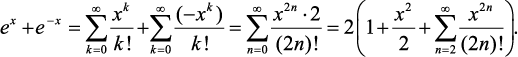(14.9)

Найдем в общем виде разницу между суммой экспонент ex + e–x и простейшей аппроксимирующей квадратичной функцией f2 = (2 + х2), рис. 14.2:

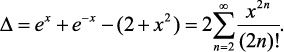(14.10)

 

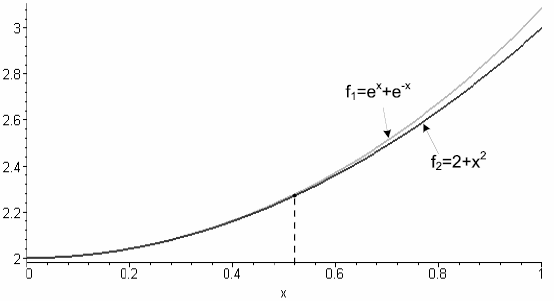
Рис. 14.2. График функций f1 и ее аппроксимации f2

При 0 ≤ x ≤ 1 получим, что абсолютная разница функций f1 и f2, рис. 14.3

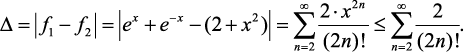(14.11)

 

 

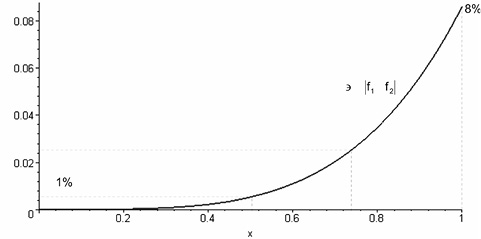
Рис. 14.3. Абсолютная погрешность квадрирования при разных Х

Определим предельное значение суммы (14.3):

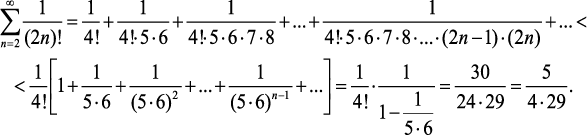(14.12)

Таким образом, абсолютная погрешность возведения в квадрат при 0 ≤ x ≤ 1 не превышает величины 0,0862 (или 8,62 %):

 

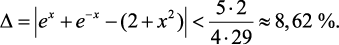
Если 0 ≤ x ≤ 0,5, то ошибка квадрирования не более 1 % (рис. 14.3).

Таким образом, если x ≤ 0,5 (ux ≤ 13 мВ), то погрешность возведения в квадрат, которую обеспечивает схема рис. 1а, Δ < 0,01 (или 1 %).

Более точное соответствие функций f1 и 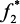 может быть получено, если обеспечить аппроксимацию суммы экспонент f1 более сложной функцией вида 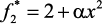(рис. 14.4), где α – постоянный множитель при x2.

 

 

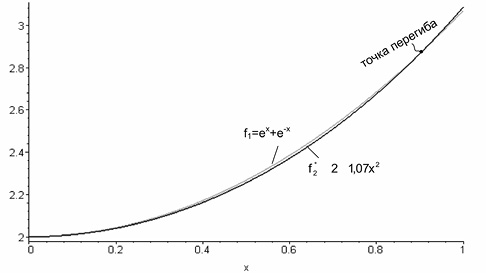
Рис. 14.4. Графики функции f1 и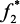 

При этом погрешности квадрирования, например при α = 1,07, оказываются несколько меньше, чем для аппроксимирующей функции вида (2 + x2) рис. 14.3.

 

 

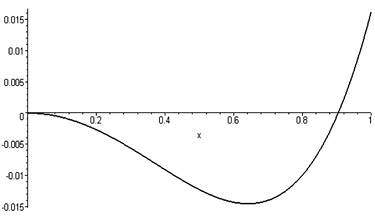
Рис. 14.5. Погрешность квадрирования при введении коэффициента α = 1,07 в модифицированную аппроксимирующую функцию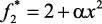

При 0 ≤ x ≤ 1 ошибка не превышает 1,5 % (рис. 14.5).

Таким образом, ток в цепях нагрузки R1 и R2 АК рис. 14.1а содержит составляющую, пропорциональную квадрату входного напряжения ux. Следовательно, схема рис. 14.1а выполняет функцию преобразования ux в выходное напряжение, пропорциональное 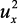. Это позволяет использовать АК в качестве удвоителя частоты ωx = 2πfx. Действительно, при синусоидальном входном сигнале ux = Uxsinωx переменный выходной сигнал uвых не содержит (в идеальном случае) первой гармоники ux и имеет удвоенную частоту 2ωx:

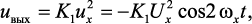(14.13)

где K1 – коэффициент пропорциональности.

При выполнении АК по схеме рис. 14.6 увеличивается коэффициент пропорциональности K1 в формуле (14.13).  

 

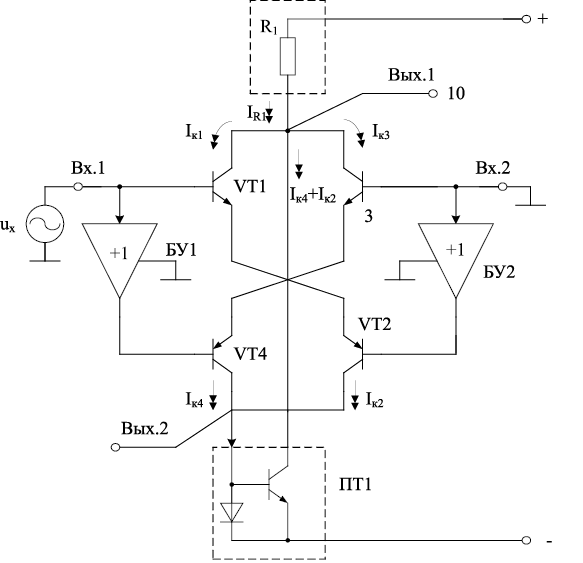
Рис. 14.6. Архитектура аналогового квадратора с повышенной крутизной

Схемотехническое решение рис. 14.7 позволяет получить напряжение в нагрузке (Rн), «привязанной» к общей шине источников питания. Это создает существенное преимущество схемы рис. 14.7 по сравнению с рис. 14.1а и 14.6.  

 

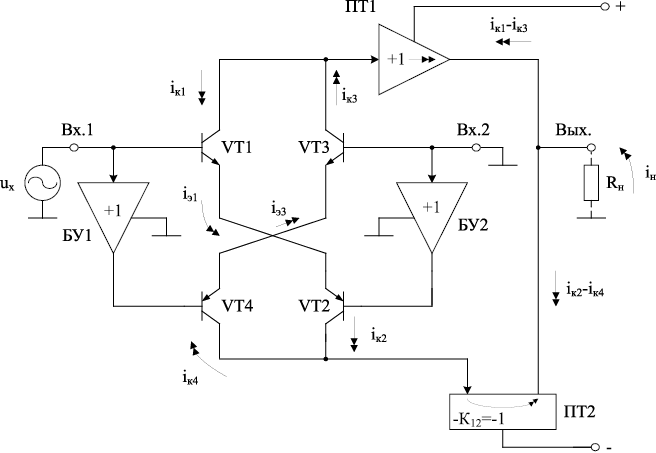
Рис. 14.7. Аналоговый квадратор с «привязанной»
к общей шинесопротивления нагрузки Rн

Таким образом, схема рис. 14.1а и ее модификации рис. 14.1б, рис. 14.6, 14.7 выполняют функцию квадратора входных сигналов и могут использоваться в структуре удвоителей частоты. На рис. 14.8–14.20 результаты моделирования.

Рассмотренные выше схемы квадраторов реализованы на базе несимметричной структуры рис. 14.1а. В этой связи представляет интерес исследование симметричных практических схем квадраторов и умножителей частоты (рис. 14.1б).

Практическая схема квадратора, соответствующая обобщенной схеме рис. 14.1б, приведена на рис. 14.21.

 

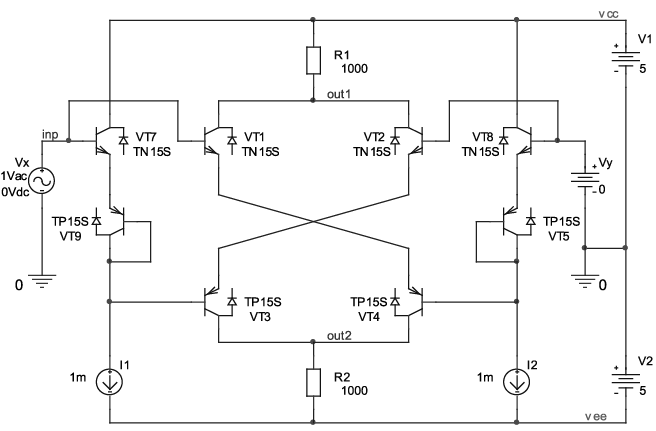
Рис. 14.8. Компьютерная модель АК рис. 14.1а в среде PSpice на основе интегральных транзисторов ФГУП НПП «Пульсар»

 

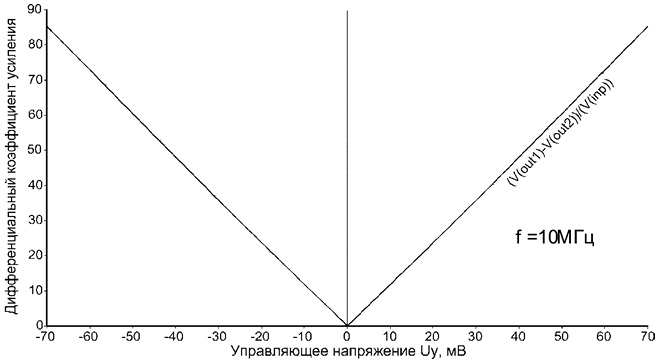
Рис. 14.9. Зависимость модуля коэффициента усиления квадратора рис. 14.8
от управляющего напряжения Uy

 

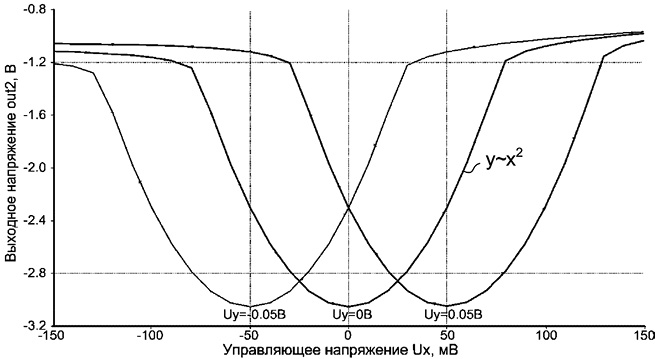
Рис. 14.10. Зависимость входного напряжения квадратора рис. 14.8 от Ux  

 

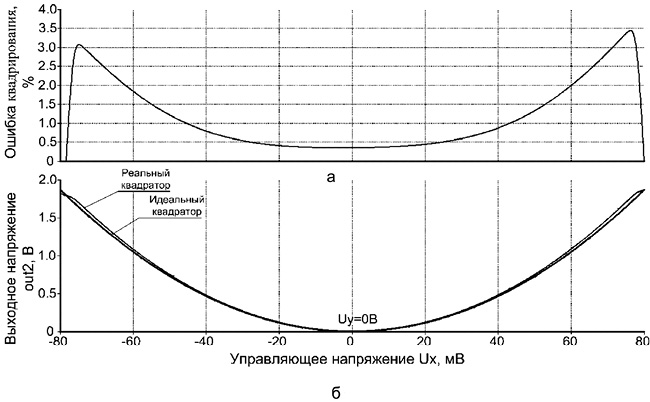
Рис. 14.11. Ошибки квадрирования АК рис. 14.8: относительная (а) и абсолютная (б)

 

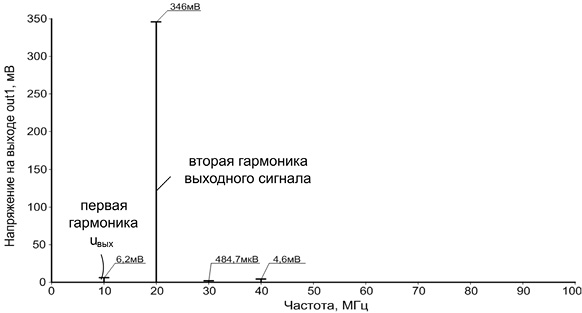
Рис. 14.12. Спектр выходных сигналов АК рис. 14.1a в режиме удвоителя частоты fx = 10 МГц при Ux = 50 мВ, Uy = 0

 

 

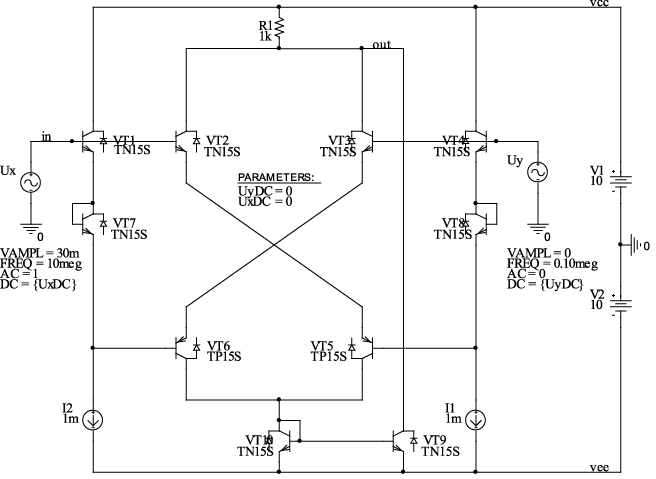
Рис. 14.13. Схем аквадратора рис. 14.6 в среде PSpice на моделях интегральных транзисторов ФГУП НПП «Пульсар»

 

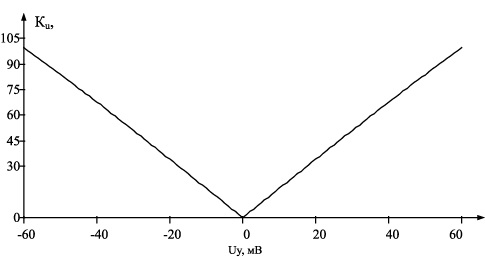
Рис. 14.14. Зависимость модуля коэффициента усиления АК рис. 14.13 от Uy

 

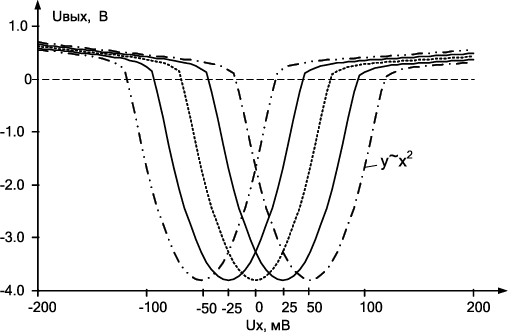
Рис. 14.15. Зависимость выходного напряжения АК рис. 14.13 от Ux

 

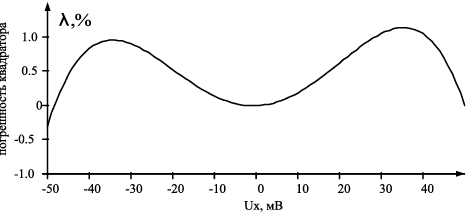
Риc. 14.16. Погрешности квадрирования Ux схемы рис. 14.13

 

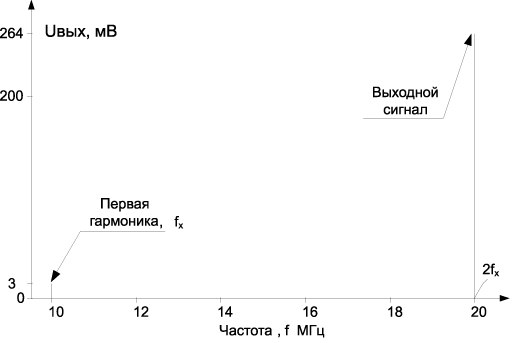
Рис. 14.17. Спектр выходного напряжения схемы АК рис. 14.13 в режиме удвоителя частоты или fx = 10 МГц Ux = 30 мВ

 

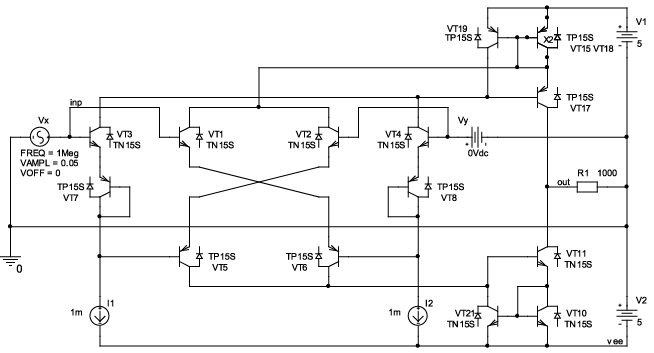
Рис. 14.18. Схема АК рис. 14.7 в среде PSpice на моделях интегральных транзисторов ФГУП НПП «Пульсар»

Соответствующая компьютерная модель показана на рис. 14.22. Здесь приняты дополнительные меры по исключению динамической перегрузки входных эмиттерных повторителей большим входным сигналом – предусмотрены корректирующие конденсаторы С1 = С2.

 

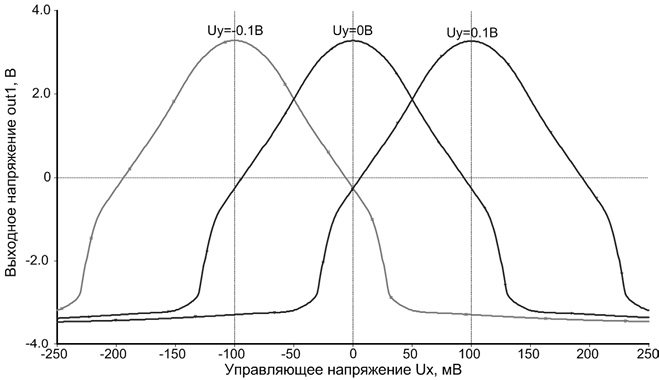
Рис. 14.19. Зависимость выходного напряжения АК рис. 14.18 от Ux

 

 

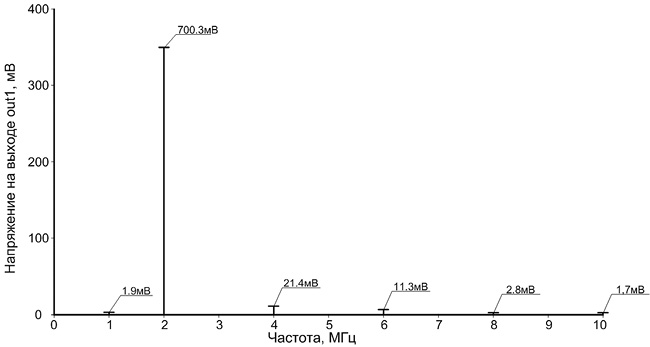
Рис. 14.20. Спектр выходного напряжения квадратора рис. 14.18 в режиме удвоителя частоты при f = 1 МГц, Ux = 0,05 В

 

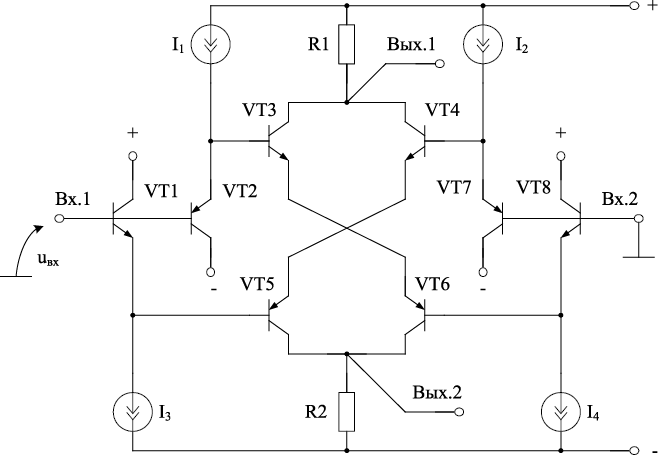
Рис. 14.21. Симметричный квадратор  

 

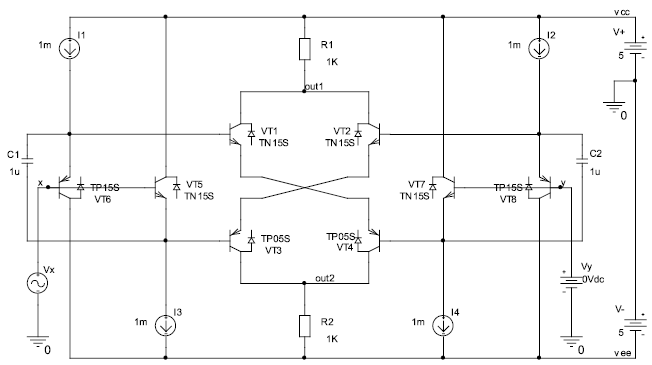
Рис. 14.22. Схема устройства

Зависимость дифференциального коэффициента усиления квадратора рис. 14.22 в режиме управляемого усилителя приведена на рис. 14.23 и  14.24.

Основная характеристика квадратора показана на рис. 14.25.

 

 

Рис. 14.23. Дифференциальный коэффициент усиления (дБ) от частоты (Гц) при разных значениях напряжения Uy от –0,1 В до 0,1 В с шагом 0,01 В

 

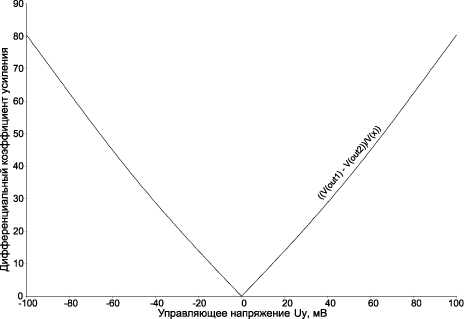
Рис. 14.24. Зависимость дифференциального коэффициента усиления от управляющего Uy от –0,1 В до 0,1 В с шагом 0,001 В на частоте 10 МГц

 

Рис. 14.25. Напряжение на выходе от напряжения Ux при разном напряжении Uy

Погрешности квадрирования приведены на рис. 14.26.

 

 

Рис. 14.26. Проходная характеристика квадратора – реального и идеального (внизу), относительная ошибка квадрирования (вверху) при Uy = 0 В, C1 = C2 ≠ 0, Uпит = ±5 В

Особенности работы симметричного квадратора в режиме удвоителя частоты характеризуют рис. 14.27–14.30.  

 

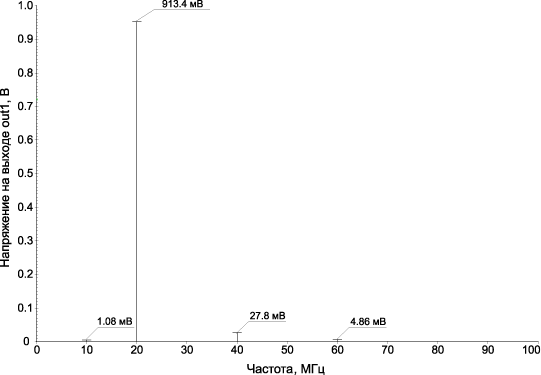
Рис. 14.27. Спектр выходного сигнала устройства в режиме удвоителя частоты при Ux = 10 МГц с амплитудой  100 мВ и управляющем напряжении Uy = 0 (C1 = C2 = 0, Uпит = ±5 В)

 

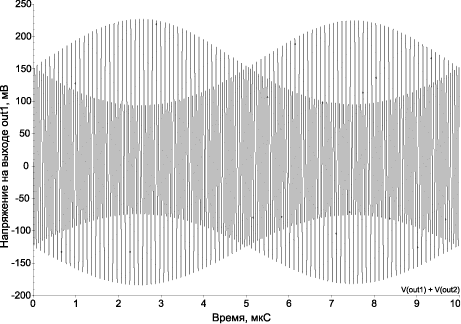
Рис. 14.28. Сумма выходных сигналов out1, out2 устройства в режиме смесителя сигналов при Ux = 10 МГц с амплитудой 100 мВ и fy = 0,1 МГц с амплитудой 25 мВ (емкости C1 = C2 ≠ 0, Uпит = ±10 В)

 

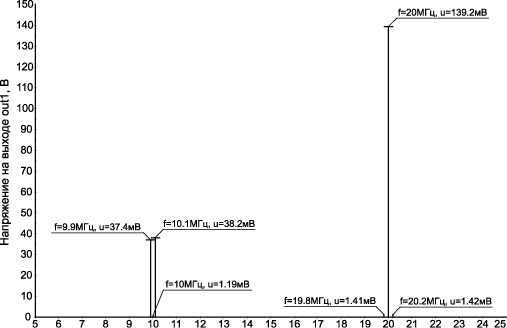
Рис. 14.29. Спектр выходных сигналов устройства в режиме смесителя сигналов при Ux = 10 МГц с амплитудой 100 мВ и fy = 0,1 МГц с амплитудой 25 мВ (C1 = C2 ≠ 0, Uпит = ±10 В)

 

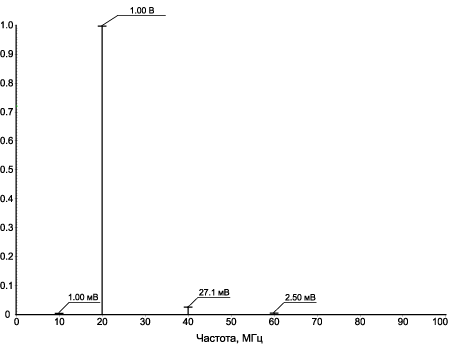
Рис. 14.30. Спектр выходного сигнала устройства в режиме удвоителя частоты при Ux = 10 МГц с амплитудой  100 мВ (Uy = 0 В; C1 = C2 ≠ 0, Uпит = ±10 В)

Таким образом, разработанные схемотехнические решения квадраторов на основе дифференциальных каскадов с нелинейной коррекцией, как показывают результаты компьютерного моделирования, обеспечивают достаточно эффективное нелинейное преобразование сигналов.