Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.5. Расчет коэффициента теплопроводности в зависимости от температуры с учетом анизотропии
Для оценки напряженно-деформированного состояния элементов турбины из эвтектических композитов и монокристаллических жаропрочных сплавов необходимо знать их теплофизические характеристики. В частности, значения коэффициента теплопроводности являются исходными данными для расчета теплового состояния лопаток газовых турбин.
В настоящее время коэффициент теплопроводности определяется различными методами. Как правило, это стационарные и нестационарные методы измерения.
Кроме того, определение коэффициента теплопроводности кристаллических тел основано на формуле, заимствованной из кинетической теории газов [48] с привлечением методов тензорного исчисления
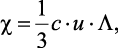
где c – теплоемкость; u – средняя скорость частиц; Λ – средняя длина свободного пробега фононов, определяемая фонон-фононным взаимодействием (по Дебаю).
Для расчета этим методом, в частности, необходимо знать среднюю длину свободного пробега фононов, что представляет сложность для инженерных расчетов.
Краткий обзор существующих методов показывает, что в настоящее время расчет коэффициента теплопроводности проводится эмпирическими или полуэмпирическими методами. Поэтому актуальным является применение теоретического метода расчета коэффициента теплопроводности для монокристаллов – составляющих материалов лопаток турбин авиационных ГТД.
Задача решается на основе формул, приведённых в разделе 1.2 и 1.4.
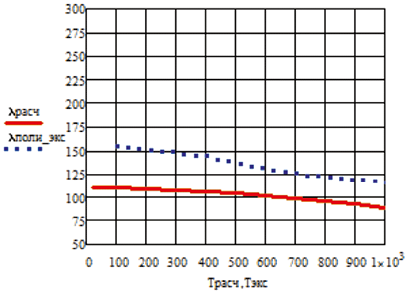
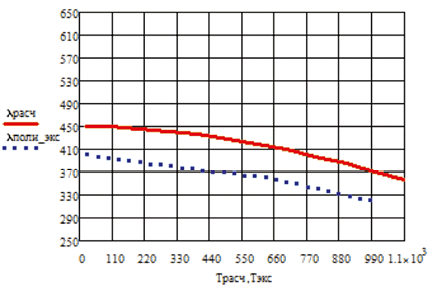
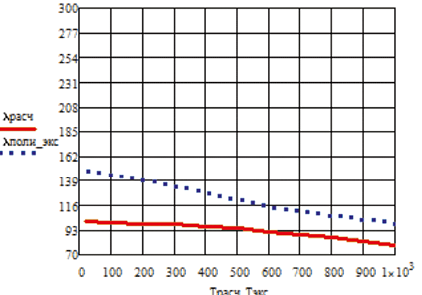
Изменение коэффициента теплопроводности расчетного и экспериментального значения в зависимости от температуры приведены на рис. 1.25 на примере Ag, Al, Cr, W, Cu, Ir.
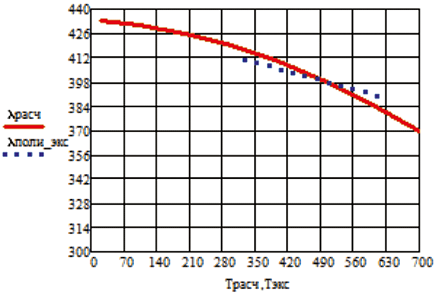
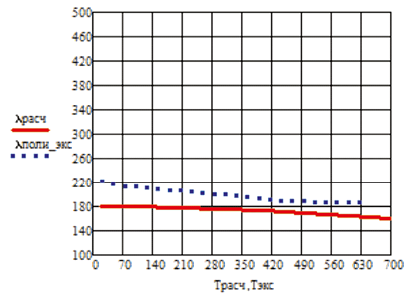
а б
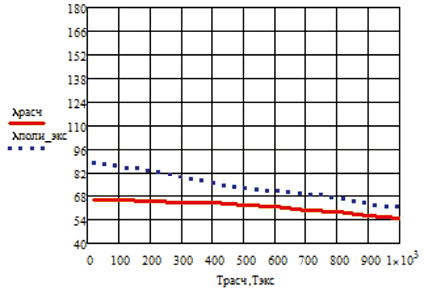
в г
д е
Рис. 1.25. Изменение коэффициента теплопроводности в зависимости от температуры:
а – Ag; б – Al; в – Cr, г – W; д – Cu; е – Ir
Приведенные на рисунке зависимости коэффициента теплопроводности от температуры подтверждают адекватность модели.
Значения коэффициентов теплопроводности волокон NbC и Ni3Al композиционных материалов NbC–Ni и Ni3Al–Ni определяется по формуле (1.17) для плотноупакованных плоскостей (100), (110), (111) и в соответствующих кристаллографических направлениях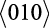 
, 
, 
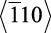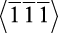. Кристаллическая структура волокна NbC представлена на рис. 1.26. Кристаллическая структура волокна Ni3Al представлена на рис. 1.27.
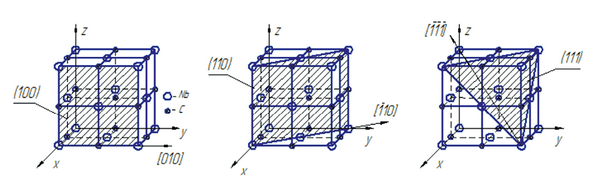
Рис. 1.26. Кристаллическая структура NbC
Рис. 1.27. Кристаллическая структура Ni3Al
При расположении волокон параллельно потоку теплоты эффективная теплопроводность λ1 для одноосно-армированных композиций определяется по формуле [35]:
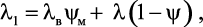
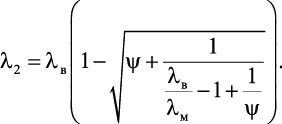
где λв и λм – теплопроводность волокон и матрицы; ψ – объемная доля волокон.
Если волокна расположены перпендикулярно потоку теплоты, то теплопроводность λ2 определяется по формуле [35] (поперек волокон):
Результаты расчета коэффициентов теплопроводности композитов
NbC–Ni и Ni3Al–Ni от объемной доли волокон приведены в табл. 1.29 и 1.30.
Таблица 1.29
Зависимость коэффициентов теплопроводности λ1 и λ2 композиционного материала NbC–Ni от объемной доли волокон
|
№ п/п |
Расчетное значение λ1, |
Расчетное значение λ2, |
Объемная доля волокон y, ٪ |
|
1 |
56,5 |
11,8 |
10 |
|
2 |
52,7 |
7,5 |
20 |
|
3 |
48,8 |
3,9 |
30 |
|
4 |
44,9 |
0,7 |
40 |
Таблица 1.30
Зависимость коэффициентов теплопроводности λ1 и λ2 композиционного материала Ni3Al–Ni от объемной доли волокон
|
№ п/п |
Расчетное значение λ1, |
Расчетное значение λ2, |
Объемная доля волокон y, ٪ |
|
1 |
59,8 |
30 |
10 |
|
2 |
59,2 |
19,8 |
20 |
|
3 |
58,6 |
12 |
30 |
|
4 |
58,04 |
5,2 |
40 |
Из таблиц видно, что значение λ2 сильно зависит от объемной доли волокон. При y больше 40 % коэффициент теплопроводности поперек волокон значительно уменьшается, что ведет к росту термических напряжений в лопатке.
Таким образом, увеличение объемной доли армирующей фазы в эвтектическом композите, с одной стороны, ведет к увеличению прочности, а с другой стороны – приводит к росту термических напряжений.
Результаты расчета коэффициента теплопроводности монокристаллов при 20 °C и температурные зависимости коэффициента теплопроводности монокристаллов имеют удовлетворительную сходимость с экспериментами других авторов. Теоретический расчет коэффициента теплопроводности монокристаллов – составляющих материалов лопаток турбин авиационных ГТД – позволяет значительно сократить объем трудоемких и дорогостоящих экспериментов.
Выводы по главе
Разработанный теоретический метод расчета и математическая модель диаграммы «напряжение – деформация» монокристаллов значительно снижают объем дорогостоящих экспериментов, в том числе на уникальном оборудовании. На основе разработанной модели выведены системы расчетных зависимостей упругих, теплофизических и прочностных характеристик материалов: модуль упругости с учетом анизотропии; коэффициент Пуассона; предел упругости, предел текучести с учетом анизотропии; коэффициент теплопроводности; коэффициент теплового расширения; модуль упругости и коэффициент теплового расширения в зависимости от температуры; плотность. Это позволило заложить основу для конструирования материалов, в том числе с использованием нанотехнологий.
Получены результаты расчета упругих и прочностных характеристик для: матриц эвтектических композитов на основе Ni, Fe, V, Nb, Ta, Cr, Mo, W; армирующих фаз типа TaC, NbC, соответствующих результатам экспериментов других авторов. Эти результаты являются начальным этапом оценки напряженно-деформированного состояния рабочей лопатки турбины. Исходные расчетные данные формируются в условиях существенного сокращения дорогостоящих экспериментов, что значительно снижает экономические и временные затраты в процессе проектирования, в частности, лопаток газовых турбин.