Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Курмангазиева Л. Т., Оразбаев Б. Б.,
1.3. Формализация и постановка задач оптимизации производства, проблемы и подходы их решения
1.3. Формализация и постановка задач оптимизации производства, проблемы и подходы их решения
Задачи математического моделирования с целью принятия решения по выбору оптимального режима работы технологических объектов современного нефтеперерабатывающего производства обычно являются многокритериальными. К основным критериям при принятия решения и управлении можно отнести повышение производительности, обеспечение желаемых качеств вырабатываемых продуктов, снижение их себестоимости, экономия материалов и ресурсов, обеспечение стабильности и улучшения экологического состояния производства, охрана окружающей среды и здоровья персонала и т.д., причем часто они бывают противоречивыми.
В зависимости от экономических (количество и качество продукции, издержки производства и другие), производственных (планы производства продуктов, график ремонта агрегатов и другие), технологических (режимные параметры процесса) и экологических (вопросы охраны окружающей среды) и других факторов эти критерии имеют разные важности, причем с изменением указанных факторов взаимная важность критериев также меняется. В данной работе основными критериями оптимизации объектов нефтепереработки являются группы экономических, технологических и экологических показателей производства.
Таким образом, задачи принятия оптимального решения при управлении технологическими объектами нефтеперерабатывающего производства, характеризующиеся многокритериальностью, сводятся к решению задач векторной оптимизации, которые позволяют найти область эффективных решений. А окончательный выбор и принятие решений может осуществлять ЛПР (лицо, принимающее решение – в нашем случае начальник цеха или установки, технолог и старшие операторы) на основе своего предпочтения, ситуаций на производстве и рынке, а также информации, полученной в диалоге с компьютерной системой поддержки принятия решений.
Для формализации и решения задач оптимизации и управления многокритериальными объектами, каким является комплекс технологических агрегатов нефтепереработки, необходимо [82, 105, 106]:
1) выявить условия работы агрегатов и их связи с другими объектами;
2) выбрать локальные критерии объекта, т.е. показатели режимов работы агрегатов и системы, которые надо оптимизировать;
3) определить управляющие параметры, изменяя которые можно добиться оптимальных значений критериев;
4) сформулировать задачу принятия решений по выбору оптимальных режимов работы технологического объекта;
5) разработать систему математических моделей технологических агрегатов, описывающих связь управляющих воздействий со значениями локальных критериев качества:
● 5.1 сбор доступных данных (теоретические, экспериментально-статистические, экспертные и нечеткие);
● 5.2 на основе собранных данных выявить типы моделей, которые могут быть построены для каждого технологического агрегата;
● 5.3 анализ и выбор типа моделей агрегатов (на основе критериев сравнения и выбора);
● 5.4 построение отдельных моделей агрегатов и их объединение в систему;
1) корректировка постановок задач ПР и управления;
2) выбор, модификация или разработка алгоритмов решения задач ПР по выбору оптимального режима работы технологических объектов;
3) разработка программного обеспечения системы поддержки принятия решений и управления технологическим комплексом.
Подпункты 5.1–5.4, этапа – разработка математических моделей агрегатов – отражают сущность предлагаемой в работе [105] методики построения математических моделей комплекса взаимосвязанных агрегатов. В данной Работе на основе этой методики будет разработана система математических моделей технологических агрегатов блока риформинга установки ЛГ Атырауского НПЗ.
Рассмотрим формальную постановку задач принятия решений по выбору оптимального режима работы комплекса технологических агрегатов. Пусть имеются связанные математические модели агрегатов технологической установки, т.е. оператор, приводящий в соответствие векторам управляющих воздействий x = (x1, …, xn) вектор выходных параметров y = (y1, …, ym)
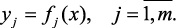(1.6)
Модели агрегатов (1.6), в зависимости от цели моделирования и от доступной информации, могут быть построены различными способами, которые описаны выше, и должны быть учтены требования, определяющие простоту объединения отдельных моделей в систему.
Критерии локальной оптимальности или частные целевые функции:
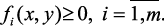(1.7)
объединяются в векторную функцию (если критерий управления единственный, то в скалярную функцию, i = 1) векторных аргументов x,y, которая выражает заинтересованность ЛПР в том или ином режиме работы объекта в зависимости от сложившейся производственной ситуации. Например, при управлении технологической установкой, вырабатывающей несколько продуктов, может быть поставлена задача увеличения выхода одних продуктов, придерживая выход остальных на определенном уровне, или повышения качества целевого продукта за счет снижения
других показателей.
При заданных х, у функции fi принимают определенные значения. Одной из задач является выбор таких векторов х,у, которые выделяют область Парето-множество, где улучшение любого из критериев fj ∈ f, j ∈ K возможно только за счет ухудшения других – f1 = f, 1 ∈ K, 1 ≠ q,
K – множество индексов.
Так как согласно (1.6), вектор у сам определяется заданием вектора х, то можно считать, что целевые функции являются функциями только от управляющих воздействий fi(x). Тогда задача принятия решения по выбору оптимального режима работы технологического комплекса ставится в виде многокритериальной задачи оптимизации режимов работы объектов управления: необходимо найти вектор управлений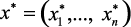 
,
обеспечивающий наилучшее приближение к желаемым значениям локальных критериев качества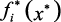 
, при выполнении ограничений, наложенных на управления и критерии.
Подходы к выбору решения в многокритериальных задачах на основе предпочтений ЛПР рассматриваются в теории принятия решений
[50, 56, 64, 69, 107–111].
Основная трудность решения проблем многоцелевого управления связана с заданием принципа оптимальности. В задачах векторной оптимизации существует много различных принципов (принципы равенства, абсолютной и относительной уступки, лексикографический принцип, принцип выделения главного критерия), каждый из которых приводит к получению различных решений. Это предъявляет серьезные требования к выбору принципа оптимальности, дающего ответ на главный вопрос – в каком смысле выбираемое решение оптимальное, т.е. лучше всех других решений.
Рассмотрим основные проблемы, связанные с решением многокритериальных задачи ПР, возникающие при выборе оптимального режима работы технологических агрегатов.
1. Проблема определения области компромисса. В задачах векторной оптимизации имеется противоречие между некоторыми из критериев. В силу этого область ΩА допустимых решений распадается на две непересекающие части: область согласия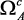 
, где противоречия между критериями отсутствуют, и область компромиссов 
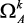, совпадающую с множеством Парето, т.е. имеются противоречивые критерии, и улучшение качества решения по одним критериям ухудшает качества решения по другим. Ясно, что рациональный режим работы установки (оптимальное решение) может принадлежать только в области компромисса, т.е. 
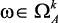, т.к. в области согласия решение может быть улучшено по нескольким критериям без ухудшения по остальным. Следовательно, поиск рациональных режимов результата этого этапа – сужение области возможных решений до множества Парето.
2. Проблема выбора схемы компромисса, позволяющей построить свертки критериев управления. Поиск рациональных режимов работы установки в области компромисса может быть осуществлен только на основе некоторой схемы компромисса. Так как число возможных схем компромисса велико, выбор конкретной схемы является сложной проблемой и обычно решается на основе предпочтений ЛПР. Выбор схемы компромисса соответствует раскрытию смысла оператора оптимизации opt в выражении:
opt f(A) = max φ(f(A)), A ∈ ΩА,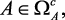 
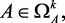(1.8)
где символами A и f обозначены значение альтернативы (А) и соответствующее ей значение вектора критериев f, φ(f) – некоторая скалярная функция от вектора критериев f, (функция свертки локальных критериев).
Таким образом, выбор того или иного принципа оптимальности сводит векторную задачу к эквивалентной скалярной задаче оптимизации.
3. Нормализация критериев. Эта проблема возникает, если, локальные критерии имеют различные единицы измерения. Необходимо нормализовать критерии, т.е. привести их к одинаковым единицам или безразмерному масштабу. К настоящему времени известно несколько различных схем нормализации [112].
4. Проблема учета приоритета критериев. Учет приоритетов критериев производится в большинстве методов свертывания путем задания вектора коэффициентов важности (весов) критериев λ = (λ1, λ2, …, λk) где λi – вес критерия fi. В результате нормализации и учета приоритетов вместо исходной векторной оценки f(A) альтернативы А, образуется новая векторная оценка:
φ(f(A)) = λ1f1(А), λ2f2(А), …, λmfm(А)), (1.9)
где fi(A),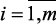 
– нормированные значения критериев.
При решении этих и других проблем, возникающих при решении многокритериальных задач ПР и разработке систем управления промышленными объектами, необходимо применение различного рода эвристических процедур, в которых существенная роль принадлежит экспертам, предпочтениям ЛПР.
Предметом исследования в данной исследовательской работе является разработка методов моделирования и принятия оптимальных решений с применением последних достижений математических методов и компьютерной технологии.
В данной работе автором предложен подход, который позволяет
формализовать и решать исходную нечеткую задачу без преобразования, сохраняя нечеткость и многокритериальность проблемы на основе модификации различных компромиссных схем приня-
тия решений.
Рассмотрим общие подходы (идею) к формализации и решению многокритериальных задач ПР по выбору оптимального режима работы объектов нефтегазового производства по эколого-экономическим критериям при наличии рассмотренных выше проблем нечеткости исходной информации.
Пусть f1(x), …, fm(x) – локальные критерии экономико-экологического характера, по которым оцениваются и выбирается оптимальный режим работы исследуемого производственного объекта – технологического комплекса переработки нефти. Каждый из этих критериев зависит от вектора n параметров (входных воздействий) х = (х1, …, хn) и может различаться своими коэффициентами относительной важности (весами) g1, …, gm.
Каждый локальный критерий fi(x) связан со значением входных воздействий, эту зависимость описывают модели исследуемого объекта.
В общем виде задачу ПР производственных объектов нефтепереработки, которая характеризуется многокритериальностью и нечеткостью исходной информации, можно формализовать в виде многокритериальных задач нечеткого математического программирования (НМП).
Пусть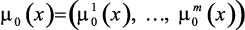 
– нормализованный вектор критериев: m0(х) = j(fi(x)), оценивающий режим работы технологического комплекса нефтепереработки с учетом экономических показателей и природоохранных мероприятий. Предположим, что функции принадлежности выполнения ограничений mq(x) для каждого ограничения fq(x) > bq, 
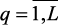построены в результате диалога с ЛПР, специалистами-экспертами. Тогда общую многокритериальную задачу ПР в нечеткой среде можно записать в следующем виде:
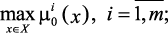(1.10)
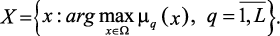(1.11)
На основе различных компромиссных схем принятия решений, принципов оптимальности можно получить семейство постановок многокритериальных задач ПР (в виде задач НМП) и предложить конкретные алгоритмы их решения. Конкретные постановки многокритериальных задач ПР в нечеткой среде, а также используемые, модифицированные и разработанные алгоритмы их решения будут приведены в последующих разделах данной монографии.