Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

РАЗРАБОТКА МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ И ОПТИМИЗАЦИЯ ХИМИКО-ТЕХНОЛОГИЧЕСКИХ СИСТЕМ ПРИ НЕЧЕТКОСТИ ИСХОДНОЙ ИНФОРМАЦИИ

Курмангазиева Л. Т., Оразбаев Б. Б.,

2.3. Разработка алгоритма синтеза моделей технологического комплекса нефтепереработки на основе лингвистической информации

В данном подразделе работы исследован комплекс технологических агрегатов блока каталитического риформинга как объект моделирования и оптимизации. Предложен алгоритм синтеза математических моделей исследуемого комплекса в нечеткой среде.

Технологический комплекс каталитического риформинга и задачи моделирования режимов его работы характеризуются сложностью. Сложность объекта исследования проявляется в значительном числе и многообразии параметров, определяющих течение процессов, в большом числе внутренних связей между параметрами, в их взаимном влиянии, в неформализуемом действии человека, участвующего в контуре управления. Кроме того, при формализации и решении задач оптимизации процесса риформинга возникает ряд проблем, связанных со множеством критериев, определяющих качество объекта.

Многокритериальность исследуемых систем затрудняет разработку математического описания процессов на основе которых осуществляется процедура оптимизации. Из-за ненадежности, недостатков или отсутствия необходимых средств сбора и обработки статистических данных, собранная информация для описания исследуемого комплекса может оказаться в значительной степени неполной, достаточно неопределенной. Проведение специальных экспериментов для сбора недостающей информации, даже при возможности их проведения, часто оказывается экономически нецелесообразным. Основным источником информации в этих ситуациях является человек (специалист-эксперт, ЛПР: технолог, оператор), который дает нечеткое описание проблемы, т.е. возникает проблема неопределенности, связанная с нечеткостью исходной информации.

В данной работе предложены и используются новые подходы и методы разработки математических моделей технологического комплекса, при наличии рассмотренных выше проблем многокритериальности и нечеткости исходной информации.

Как известно, при моделировании и оптимизации сложных систем в условиях неопределенности используется вероятностный подход, основанный на методах теории вероятностей и математической статистики. Однако, на практике не всегда при наличии неопределенностей выполняются аксиомы теории вероятностей, что показывает неправомерность применения этих методов. Более того, в случаях, когда есть основания считать, что процессы или системы ведут себя по вероятностным законам, дефицит информации, невозможность или дороговизна получения достоверной статистической информации толкают на иные пути описания реальных процессов в производственных системах, на разработку нестатистических, например, нечетких методов моделирования объектов. Один из перспективных путей в этом направлении опирается на методы теории нечетких множеств [86, 94, 120–122, 148, 149].
Таким образом, проблему неопределенности можно решить созданием математического аппарата для описания и исследования нечетко
определенных объектов.

Можно выделить следующие подходы к моделированию объектов, удовлетворяющие этим требованиям, которые основаны на методах теории нечетких множеств [36, 150, 151]:

1. Подход, основанный на построении статистических моделей объектов с нечеткими коэффициентами на основе модификации методов регрессионного анализа. Модели, полученные на основе такого подхода, успешно используются при моделировании и управлении рядом технологических объектов нефтеперерабатывающей промышленности.

Предположим, что в результате наблюдения объекта или проведенного эксперимента получено Lxi (xil, 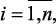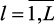) значения входных параметров, а соответствующие нечеткие значения выходных параметров 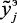(yil, 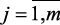, 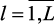) оценены экспертами, т.е. входные параметры системы измеримы и доступны их количественные значения, а выходные параметры нечеткие, т.е. оцениваются (измеряются) специалис-
тами-экспертами.

Для построения математической модели этого объекта необходимо решить следующие два этапа задачи идентификации:

а) выбрать структуру функции (структурная идентификация)

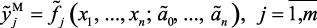(2.1)

аппроксимирующую функцию .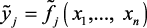

На этом этапе определяющее значение имеет качественный анализ объекта, в результате которого выявляются основные параметры, влияющие на функционирование, их взаимосвязи и выбирается метод для идентификации структуры модели;

б) Определить оценки параметров выбранной функции (2.1) (параметрическая идентификация), например значений нечетких коэффициентов 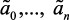. Для подобной оценки можно воспользоваться критерием минимизации отклонения нечетких значений выходного параметра 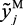, полученных по модели (2.1), от его выборочных нечетких значений, полученных на основе экспертной оценки .

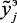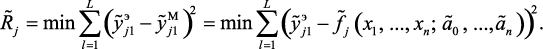(2.2)

На втором этапе основным вопросом является выбор способа оценивания неизвестных параметров, обеспечивающего необходимые свойства исследуемого объекта.

В этом подходе математические модели, полученные с учетом нечеткости исходной информации, имеют следующий общий вид:

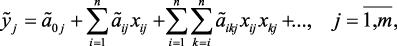(2.3)

где 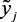– нечеткие выходные параметры системы (локальные критерии); xij, xkj – входные измеряемые параметры моделируемой системы (управляющие воздействия); 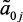, , 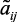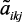– оцениваемые нечеткие коэффициенты.

Использование понятия множество уровня a позволяет свести нечеткие уравнения регрессии к системе обычных уравнений регрессии. Такой подход дает возможность применения классических методов регрессии для решения рассмотренных выше задач.

2. Подход, основанный на использовании логических правил условного вывода, например, в следующем виде:

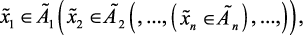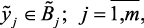if then (2.4)

где 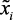, , 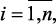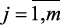– соответственно, входные и выходные лингвистические переменные объекта, влияющие на технико-экономические и экологические показатели объекта, 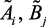– нечеткие подмножества, характеризующие .

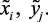Здесь и входные и выходные параметры системы 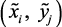характеризуются нечеткостью, т.е могут быть лингвистическими переменными. Преимуществом такого подхода является возможность его использования при моделировании объектов, для которых сбор статистической информации (xi, yj) стоит очень дорого, затруднен или невозможен. В этом случае полученные нечеткие модели являются результатом обработки экспертного опроса специалистов-экспертов (технологи, операторы, ЛПР), оперирующих, как правило, информацией качественного характера (опыт, знания). Такая информация, при условии достаточной компетентности специалистов-экспертов, позволяет в полученных моделях учесть всю гамму сложных внутренних взаимосвязей параметров объекта.

К достоинствам методов построения нечетких моделей можно отнести: следующее они позволяют получить эффективные модели объекта в условиях неопределенности, когда традиционные подходы не дают существенных результатов; в моделях, полученных на основе этих подходов, учитываются внутренние, содержательные связи основных параметров системы, которые не подлежат формализации. Однако при построении нечетких моделей возникают свои специфические проблемы, например, связанные с проведением экспертного опроса, построением функции принадлежности нечетких параметров, определением структуры условного логического вывода и т.д.

3. При построении моделей системы, представляющей собой комплекс взаимосвязанных агрегатов различного типа (технологические установки) с различной исходной информацией, приходится использовать комбинированную информацию. В этом случае модели отдельных объектов в системе могут быть построены разными методами, причем должна быть учтена возможность объединения этих моделей в пакет для моделирования работы системы в целом. На практике, при исследовании некоторого объекта, статистические данные для оценки одних
параметров могут быть достаточны, а для других параметров – недостаточны или вообще отсутствовать. Параметры таких объектов оцениваются методами, основанными на использовании информации различного характера и объединяющими вышеописанные методы и традиционные подходы к анализу систем.

Рассмотрим вопросы алгоритмизации разработки моделей количественно трудноописываемых объектов с учетом нечеткой информации. Авторами работы [119] предложен алгоритм синтеза математических моделей с учетом нечеткости выходных параметров объекта. На основе данного алгоритма структура модели идентифицируются в виде нечетких уравнений множественной регрессии с нечеткими коэффициентами. В указанной работе предложена методика параметрической идентификации нечетких коэффициентов регрессии и предложенный алгоритм и методика апробированы при разработке математических моделей станций подогрева нефти узла Атырау магистрального нефтепровода Узень-Атырау-Самара.

В результате анализа и обобщения возможных подходов моделирования сложных объектов при нечеткости исходной информации в данной работе разработан алгоритм синтеза моделей технологического комплекса при нечетких входных и выходных параметров, который использует логические правила условного вывода и реализует второй подход нечеткого моделирования и позволяет построить лингвистические модели в нечеткой среде. Приведем основные этапы предложенного алгоритма.

Алгоритм ЛМ

В этом алгоритме учитываются нечеткость и входных – 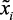, , 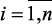и выходных 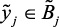, 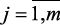параметров.

1. Выбрать необходимые для построения модели входные 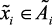, 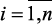и выходные 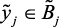, 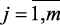параметры объекта, которые являются лингвистическими переменными (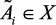 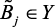– нечеткие подмножества).

2. На основе экспертных процедур произвести оценку значений параметров 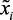, 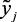и построить терм-множество .

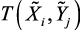3. Построить функции принадлежности нечетких параметров
, .

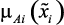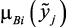4. Построить лингвистическую модель системы и формализовать нечеткие отображения, определяющие связь между 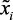и 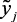– Rij.

5. Определить нечеткие значения выходных параметров объекта и выбрать их числовые значения из нечеткого множества решений.

6. Проверить условие адекватности модели. Если условие выполняется, то модель рекомендуется для использования при оптимизации и управления объектом, в противном случае определить и вернуться к предыдущим пунктам для уточнения модели.

Дадим некоторые пояснения к основным пунктам предложенного алгоритма.

В первом пункте, в зависимости от требуемой точности, выбираются наиболее информативные переменные, которые характеризуют качество работы исследуемого объекта. Для удобства диапазоны изменения нечетко описываемых параметров задаются в виде отрезков, с указанием минимального (хmin, ymin) и максимального (хmax, ymax) значения. Эти отрезки, в зависимости от суждений специалистов – экспертов, разбиваются на несколько интервалов дискретизации (кванты):

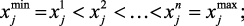
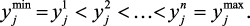
Для построения терм-множества (пункт 2) состояний каждый квант выбранных параметров словесно характеризуется соответствующими нечеткими терминами. Например, если 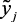– степень загрязнения окружающей среды, то его можно описать через термы:

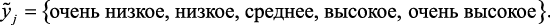
Принятое терм-множество является совокупностью значений лингвистических переменных, описывающих работу исследуемого объекта. Каждый интервал дискретизации, получаемый в первом пункте, характеризуется определенным термом. Этому терму соответствует нечеткое множество, которое описывается функцией принадлежности на соответствующем ей уровне градации.

Построение функции принадлежности нечетких множеств – параметров (пункт 3) является одним из основных этапов при моделировании сложных объектов с применением методов теории нечетких множеств. Основным способом восстановления аналитического вида этой функции является графическое построение кривой степени принадлежности того или иного параметра соответствующему нечеткому множеству. На основе полученного графика подбирается такой вид функции, который наилучшим образом аппроксимирует его. После этого идентифицируются параметры выбранной функции.

Лингвистическая (качественная) модель объекта строится по результатам обработки экспертной информации (пункт 4). Для удобства ее можно оформить в виде таблицы, где словесно (нечетко) указаны различные значения входных параметров 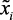и соответствующие этим
вариантам значения выходных параметров – 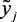. Таблица должна заполняться с использование выбранного терм-множества. На основе модели, полученной таким образом, формализуются нечеткие отображения Rij, определяющие связь между выходными и выходными параметрами.

Нечеткие отображения для кванта р можно определить следующим образом: 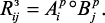Для удобства применения нечеткого отображения Rij. в расчетах нужно построить матрицы нечетких отношений – 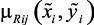, например, в общем случае для выделенных квантов:

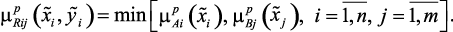(2.5а)

Пятый пункт данного алгоритма синтеза нечетких моделей заключается в применении композиционного правила вывода:

Bj = Ai°Rij.

С помощью этого правила можно осуществлять расчет выходных переменных, например, на основе максиминного произведения:

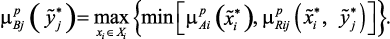(2.5б)

Пусть 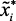– измеренные (оцененные экспертами) значения входных переменных, тогда искомое множество, которому принадлежат текущие измеряемые значения входных переменных, определяется как множество для которого измеряемые значения имеют наивысшую (максимальную) степень принадлежности:

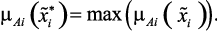(2.5в)

Прогнозируемые значения выходных переменных (нечеткие значения) определяются в виде соответствующих функций принадлежностей.

Конкретные числовые значения выходных параметров 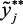из нечеткого множества решений определяются из следующего соотношения:

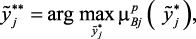
т.е. выбираются те значения входных параметров, для которых достигается максимум функции принадлежности.

Задачей заключительного этапа алгоритма (пункт 6) является проверка соответствия модели объекту. Модель считается адекватной моделируемому объекту, если найденные с ее помощью на ЭВМ характеристики объекта совпадают с заданной степенью точности, реальными данными, полученными экспериментально на самом объекте.

Как правило, в качестве критерия адекватности, являющегося мерой соответствия модели объекту, используется величина рассогласования расчетных (модельных) yM и реальных (экспериментальных) – yэ данных: R = |yM – yэ|. Кроме того, выбирается величина допустимого уровня рассогласования – RД. Модель считается адекватной, если R = |yM – yэ| ≤ RД.

В случае неадекватности математическая модель дорабатывается, определяются источники неадекватности. Это может быть недооценка значимости какой-нибудь существенной переменной и недоучет ее в модели, неправильная или неполная структура нечетких уравнений, ошибка при параметрической идентификации и т.д. После этого осуществляется возврат к соответствующему пункту алгоритма для доработки модели.

При достаточном количестве теоретических сведений и статистических данных построение моделей отдельных агрегатов технологического комплекса можно осуществлять соответственно на основе аналитических и экспериментально-статистических методов. Однако, как показывает практический опыт, во многих случаях, вследствие нехватки и нечеткости исходной информации, эти подходы неприемлемы.