
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.5. Построение моделей основных агрегатов блока каталитического риформинга установки ЛГ
Конкретизацию и реализацию вышепредложенных теоретических результатов исследований проводим на примере разработки математических моделей основных технологических агрегатов блока каталитического риформинга установки ЛГ Атырауского НПЗ. Исследуем основные параметры этого блока и их влияние на технологический процесс [113], на основе которых строятся математические модели и пакет моделей технологических агрегатов блока риформинга установки ЛГ.
Температура реактора. Температура, поддерживаемая в слое катализатора блока риформинга, является главным контролируемым параметром, который используется нефтепереработчиком для получения продукта заданного качества. Катализаторы платформинга могут работать в широком диапазоне температур не вызывая значительных отклонений от требуемого уровня выхода продукта и стабильности катализатора. Однако очень высокие температуры свыше 543 °С могут привести к термическим реакциям, которые будут снижать выход платформата и стабильность катализатора.
Для определения температуры в реакторе можно пользоваться двумя показателями: средневзвешенной температурой на входе в реактор (CТВР) и средневзвешенной температурой катализаторного слоя (СТКС). Эти величины могут быть рассчитаны следующим образом:
СТВР = СВкс⋅ТВк,
где СВкс – суммарный вес фракций катализатора в слое; ТВк – значение температуры на входе в слой катализатора;
СТКС = СВкс⋅ТСр,
где – ТСр – значение средней температуры на входе и выходе реактора.
Скорость подачи сырья. Скорость подачи измеряет количество сырья, которое пропускается через данное количество катализатора за единицу времени. Если известна часовая объемная производительность по сырью и объем загруженного катализатора, то можно найти объемную скорость подачи, если же известны соответствующие весовые показатели, те можно определить весовую скорость подачи сырья.
Скорость подачи сырья оказывает решающее влияние на качество продукта (например, октановое число). Чем выше скорость подачи, тем ниже октановое число (МОЧ), или тем меньше количество реакций произойдет при данной СТВР. При очень низких скоростях подачи ускоряются реакции термокрекинга приходящие к снижению входа платформата. Поскольку верхняя граница скорости подачи не лимитирована, чтобы получить продукт заданного качества, необходимо увеличить температуру, что в свою очередь тоже может ускорить нежелательные термические реакции приводящие к снижению селективности процесса.
Давление в реакторе. Давление в реакторе является самой точно определяемой величиной, также как и давление в слое катализатора. Поскольку около 50 % объема загруженного катализатора сосредоточены, как правило, в последнем реакторе, самым точным значением будет давление на входе в последний реактор. Давление в сепараторе в качестве эксплуатационного параметра является лимитирующей величиной, поскольку падение давления от установки к установке может значительно различаться и даже в одной и той же установке падение давления будет значительно варьироваться с изменением производительности по сырью, скорости циркулирующего ВСГа, его плотности и т.п.
Давление в реакторе влияет на выход продуктов на установке платформинга, требуемую температуру и стабильность катализатора. При снижении давления в реакторе будет увеличиваться выход платформинга и водорода, снижаться температура, необходимая для получения заданного качества продуктов и сокращаться межрегенеративный срок службы катализатора (увеличиваться скорость закоксовывания катализатора).
Соотношение водород/сырьё. Соотношение водород/сырьё (Н2/сырье) определяется как частное отделения количества молей циркулирующего водорода на число молей загруженной в установку нафты. Рециркуляция водорода в процессе платформинга необходима для поддержания стабильности катализатора.
В процессе рециркуляции продукты реакции и конденсируемые вещества смываются с поверхности катализатора, и к его освободившимся активным центрам доставляется водород. Повышение соотношения
Н2/сырье будет ускорять прохождение нафты через реактор и способствовать большей подаче тепла для эндотермических реакций. Конечным результатом этого будет увеличение стабильности наряду с небольшим положительным влиянием на выход или качество продукта.
Свойства перерабатываемого сырья. Свойства сырья, являющиеся одним из существенных вопросов при обсуждении технологических параметров включая свойства: фракционный состав: начало кипения; 50 % точка кипения (разгонка); содержание % (об.) парафинов (Р) и нафтенов (N) – метод определения PIONA.
В сырье с низким началом кипения ниже 77 °С обычно содержится значительное количество углеводородов С5 и выше. Пентаны в сырье не смогут превращаться в ароматические углеводороды, и поэтому при прохождении через реакционную зону они претерпевают только реакции изомеризации, если крекинга в лёгкие газы. Вследствие их низкого октанового числа они снижают октановую характеристику всего платформата в целом и приводят к необходимости поддержания более жесткого режима процесса платформинга, чем предполагавшаяся в случае получения риформинга С4 и выше.
В сырье с низкими температурами конца кипения содержатся высокие концентрации С6 и С7, которые наиболее трудно вступают в реакцию риформинга. Сырьё с высокой температурой конца кипения приводит к быстрому закоксовыванию катализатора, они также способствуют образованию платформинга с высокой температурой конца кипения.
Математические модели реакторов риформинга Р-2, Р-3, Р-4,4а. На основе приведенных результатов исследований разрабатываем математическое описание и модели агрегатов. В основу математической модели реакторов риформингга Р-2, Р-3, Р-4,4а положены статистические данные, экспертная информация, обработанные методами ТНМ, а также уравнения материального и теплового балансов.
Например, в результате обработки экспериментально-статистических и экспертных данных, а также применяя идею метода последовательного включения регрессоров, на основе алгоритмов НМ [119] и ЛМ [123] синтеза математических моделей в нечеткой среде получена следующая структура системы уравнений множественной, качественной регрессии и условного логического вывода, являющихся моделями реакторов риформинга [124]:
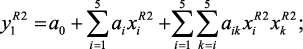 (2.6)
(2.6)
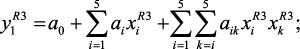 (2.7)
(2.7)
 (2.8)
(2.8)
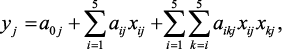 j = 2,3; (2.9)
j = 2,3; (2.9)

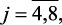 (2.10)
(2.10)
где 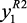 ,
, 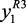 ,
, 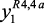 – соответственно, объем катализата с выхода реакторов Р-2, Р-3 и Р-4,4а; yj, j = 2, 3 – соответственно объем сухого газа и ВСГ;
– соответственно, объем катализата с выхода реакторов Р-2, Р-3 и Р-4,4а; yj, j = 2, 3 – соответственно объем сухого газа и ВСГ; 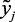 ,
,
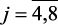 – качественные показатели катализата, соответственно, октановое число (
– качественные показатели катализата, соответственно, октановое число (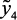 – не менее 86 по моторному методу), фракционный состав (
– не менее 86 по моторному методу), фракционный состав (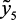 – 10 % отгонка – не выше 70 °С,
– 10 % отгонка – не выше 70 °С, 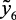 – 50 % – не выше 115 °С), давление насыщенных паров (
– 50 % – не выше 115 °С), давление насыщенных паров (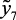 – не более 500 мм рт.ст.), содержание фактических смол в мг на 100 мл. бензина (
– не более 500 мм рт.ст.), содержание фактических смол в мг на 100 мл. бензина (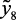 – не более 5,0); x1 – сырье – гидрогенизат с блока гидроочистки (50–80 м3/ч); x2 – объемная скорость в реакторах (1,0–1,5 ч–1);
– не более 5,0); x1 – сырье – гидрогенизат с блока гидроочистки (50–80 м3/ч); x2 – объемная скорость в реакторах (1,0–1,5 ч–1); 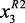 ,
, 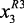 ,
, 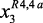 – соответственно: температура в реакторах Р-2 (470–510 °С), Р-3 (480–520 °С) и Р-4,4а (490–525 °С);
– соответственно: температура в реакторах Р-2 (470–510 °С), Р-3 (480–520 °С) и Р-4,4а (490–525 °С); 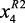 ,
,
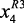 ,
, 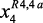 – соответственно: давление в реакторах Р-2 (25–39 кг/см2); Р-3 (22–35 кг/см2) и Р-4,4а (20–30 кг/см2); x5 – соотношение Н2/сырье (300–500 нм3); a0j, aij, aikj и
– соответственно: давление в реакторах Р-2 (25–39 кг/см2); Р-3 (22–35 кг/см2) и Р-4,4а (20–30 кг/см2); x5 – соотношение Н2/сырье (300–500 нм3); a0j, aij, aikj и 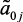 ,
, 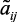 ,
, 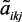 ,
, 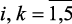 – идентифицируемые коэффициенты регрессии (четкие и нечеткие со знаком ~), соответственно: свободный член; учитывающие линейные влияния (xij), квадратные и взаимные влияния (xij, xkj), на выходные параметры реактора.
– идентифицируемые коэффициенты регрессии (четкие и нечеткие со знаком ~), соответственно: свободный член; учитывающие линейные влияния (xij), квадратные и взаимные влияния (xij, xkj), на выходные параметры реактора.
Как видно, модели описывающие выход продукции блока имеют вид множественной регрессии, соответственно идентифицированы экспериментально-статистическими методами, а модели оценивающие качества катализата имеют вид нечетких уравнений регрессии и получены на основе качественной информации от специалистов-экспертов.
Идентификация коэффициентов регрессии в моделях (2.6)–(2.9) осуществлены известными методами параметрической идентификации, на основе методов наименьших квадратов с применением пакета программ REGRESS (Кузнецов А.Г., Оразбаев Б.Б. МИСиС).
Результаты параметрической идентификации моделей, определяющих зависимость выхода катализата с реакторов, а также выхода ВСГ от режимных параметров имеют вид (2.11)–(2.14):
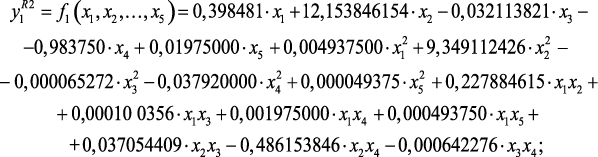 (2.11)
(2.11)
 (2.12)
(2.12)
 (2.13)
(2.13)
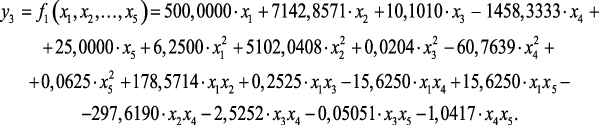 (2.14)
(2.14)
На рис. 2.2 приведена график зависимости выхода катализата с Р-4,4а от температуры реактора.
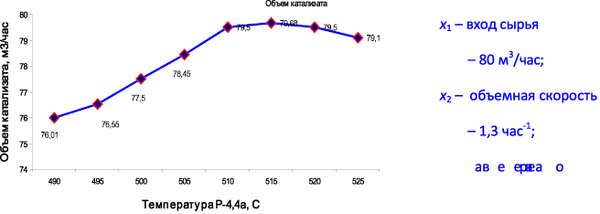
Рис. 2.2. График зависимости у1 = f1(х3), х1,х2, х4, х5 – константы
Для идентификации неизвестных нечетких коэффициентов 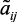
(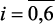 ) и
) и 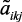 (
(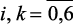 ,
, 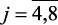 ) в уравнениях (2.10) нечеткие множества, описывающие качественные показатели продукции, разбиты на следующие множества уровня α = 0,5; 0,75; 1. В соответствии с выбранным
) в уравнениях (2.10) нечеткие множества, описывающие качественные показатели продукции, разбиты на следующие множества уровня α = 0,5; 0,75; 1. В соответствии с выбранным
уровнем наблюдается значения входных хij (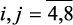 ) и выходных
) и выходных 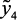 ,
, 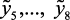 , параметров на каждом уровне αq (
, параметров на каждом уровне αq (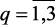 ), которые представлены в табл. Б1, приложения Б. В этой таблице приведены детерминированные значения входных и выходных параметров на каждом выбранном уровне αq.
), которые представлены в табл. Б1, приложения Б. В этой таблице приведены детерминированные значения входных и выходных параметров на каждом выбранном уровне αq.
Для каждого уровня αq моделей качественных показателей катализата (2.10), можно представить в виде системы уравнения множественной регрессии [129], тогда задача идентификации их коэффициентов 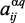
(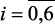 ,
, 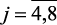 ,
, 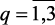 ) сводится к классическим задачам оценивания параметров множественной регрессии. Для решения последней задачи можно использовать известные алгоритмы или стандартные программы множественной регрессии, входящие в математическое обеспечение ЭВМ. Нами применен вышеиспользованный пакет программ REGRESS.
) сводится к классическим задачам оценивания параметров множественной регрессии. Для решения последней задачи можно использовать известные алгоритмы или стандартные программы множественной регрессии, входящие в математическое обеспечение ЭВМ. Нами применен вышеиспользованный пакет программ REGRESS.
Полученные значения коэффициентов 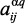 (
(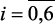 ,
, 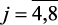 ,
, 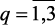 ) модели (2.10) объединены с использованием следующего соотношения
) модели (2.10) объединены с использованием следующего соотношения
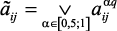
или 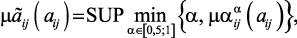
где 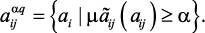
Таким образом, математические модели, описывающие нечеткую зависимость качественных показателей катализата (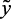 ,
, 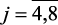 ) от входных параметров (хi,
) от входных параметров (хi, 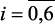 ), имеют вид:
), имеют вид:


Аналогично у5 определена 50 % отгонка – 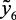 и давление насыщенных паров –
и давление насыщенных паров – 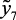 , а содержание фактических смол в мг. на 100 мл. бензина –
, а содержание фактических смол в мг. на 100 мл. бензина – 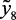 идентифицирована следующим образом:
идентифицирована следующим образом:

Исследованы влияния других режимных параметров на выходные параметры, в том числе на многомерном пространстве.
Исследование и построение лингвистических моделей процесса каталитического риформинга.
Для определения оптимальной температуры процесса риформинга на основе предложенного выше алгоритма ЛМ, логического правила условного вывода и базы знаний построена лингвистическая модель, описывающей влияние температуры реактора риформинга на выход катализата и стабильность катализатора. Эта модель реализует лингвистическую зависимость «Если TR низкая, то выход y1 низкий, стабильность y2 ниже нормы, если TR средняя, то y1 средний, y2 нормальная, если TR высокая, то y1 выше среднего, y2 выше нормы, если TR очень высокая, то y1 ниже среднего, y2 ниже нормы», где TR – температура реактора, y1 – объем катализата с реактора, y2 – стабильность катализатора.
На основе экспертных процедур и применяя аналитическую зависимость, предложенной в работе [129], определены функции принадлежности, описывающие нечеткие множества:
– mА(T) = exp(|(Т – 485)⋅0,5|) – низкая температура реактора;
– mА(Т) = exp(|Т – 495)⋅0,5|) – средняя температура реактора;
– mА(Т) = exp(|Т – 520)⋅0,6|) – высокая температура реактора;
– mА(Т) = exp(|Т – 545)⋅0,7|) – очень высокая температура реактора;
– mВ(y1) = exp(|y1 – 65)⋅0,4|) – низкий выход катализата;
– mВ(y1) = exp(|y1 – 70)⋅0,6|) – средний выход катализата;
– mВ(y1) = exp(|y1 – 75)⋅0,7|) –выход катализата выше среднего;
– mВ(y1) = exp(|y1 – 67)⋅0,5|) –выход катализата ниже среднего;
– mВ(y2) = exp(|y2 – 70)⋅0,3|) –стабильность катализатора ниже нормы;
– mВ(y2) = exp(|y2 – 90)⋅0,5|) –стабильность катализатора нормальная;
– mВ(y2) = exp(|y2 – 95)⋅0,7|) –стабильность катализатора выше нормы;
– mВ(y2) = exp(|y2 – 90)⋅0,5|) –стабильность катализатора нормальная;
Применяя структуру лингвистической модели (2.4) и модифицируя ее применительно к нашим условиям, на основе разработанного выше алгоритма ЛМ получена следующая лингвистическая модель:
if 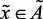 (нк), then
(нк), then 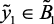 (нк),
(нк), 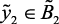 (нн);
(нн);
if 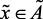 (ср), then
(ср), then 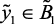 (ср),
(ср), 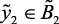 (нр);
(нр);
if 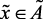 (вк), then
(вк), then 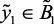 (вс),
(вс), 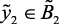 (вн);
(вн);
if 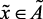 (овк), then
(овк), then 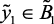 (нс),
(нс), 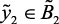 (нн), (2.15)
(нн), (2.15)
где нк, нн, ср, нр, вк, вс, вн, овс, нс – нечеткие переменные, описывающие, соответственно, понятия «низк-ая,-ий», «ниже нормы», «средн-яя,-ий», «нормальная», «высокая», «выше среднего», «выше нормы», «очень высокая», «ниже среднего»; 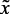 ,
, 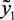 ,
, 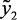 – лингвистические входные и выходные переменные, описывающие, соответственно, температуру реактора, объема катализата и стабильность катализатора;
– лингвистические входные и выходные переменные, описывающие, соответственно, температуру реактора, объема катализата и стабильность катализатора; 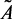 ,
, 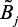 , j = 1, 2 – нечеткие подмножества, характеризующие
, j = 1, 2 – нечеткие подмножества, характеризующие 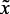 ,
, 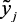 , j = 1, 2.
, j = 1, 2.
Результаты формализации нечеткого отображения, определяющие связь между 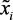 и
и 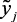 – Rij, определения качественных значения параметров объекта и их числовых значений из нечеткого множества решений приведены в приложении В.
– Rij, определения качественных значения параметров объекта и их числовых значений из нечеткого множества решений приведены в приложении В.
Аналогично идентифицируем структуру лингвистической модели, описывающей влияние скорости подачи сырья на количество и качество (октановое число) целевой продукции блока риформинга – катализата, которая описывает логический вывод «Чем выше скорость подачи, тем ниже октановое число и выше выход катализата».
if 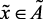 (нк), then
(нк), then 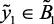 (вк),
(вк), 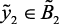 (нк),
(нк),
if 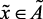 (ср), then
(ср), then 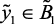 (ср),
(ср), 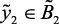 (ср),
(ср),
if 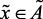 (вк), then
(вк), then 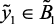 (нк),
(нк), 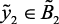 (вк) (2.16)
(вк) (2.16)
где нк, вк, ср, – нечеткие переменные, описывающие, соответственно, понятия «низк-ая, -ий, ое», «высок-ое, ая, -ий», «средн-яя,-ое,-ий»; 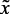 ,
, 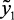 ,
,
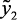 – лингвистические входные и выходные переменные, соответственно, скорость подачи сырья, октаное число и объем катализата.
– лингвистические входные и выходные переменные, соответственно, скорость подачи сырья, октаное число и объем катализата.
По результатам исследований и обработки результатов экспертных процедур получена следующая структура лингвистической модели, оценивающей влияние давления в реакторе на выход катализата и ВСГ, на температуру и на срок службы катализатора.
if 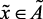 (нк), then
(нк), then 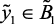 (вк),
(вк), 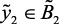 (вк),
(вк), 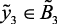 (нк),
(нк),
if 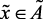 (нр), then
(нр), then 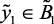 (ср),
(ср), 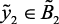 (ср),
(ср), 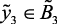 (ср),
(ср),
if 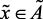 (вк), then
(вк), then 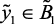 (нк),
(нк), 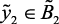 (вк),
(вк), 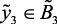 (вс) (2.17)
(вс) (2.17)
где нк, вк, нр, ср – нечеткие переменные, описывающие, соответственно, понятия «низк-ое, -ий», «высок-ий ,-ое», «нормаль-ное», «средн-ий, -ое»; 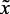 ,
, 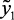 ,
, 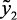 ,
, 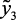 – лингвистические входные и выходные переменные, соответственно, давление (
– лингвистические входные и выходные переменные, соответственно, давление (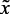 ), объем катализата (
), объем катализата (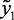 ), водорода (
), водорода (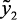 ) и качество катализата (
) и качество катализата (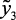 ),
), 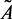 ,
, 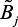 ,
, 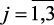 – нечеткие подмножества, характеризующие
– нечеткие подмножества, характеризующие 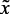 ,
, 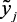 ,
, 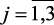 .
.
Математическая модель печи риформинга П-1. Многокамерная печь риформинга П-1 предназначена для восстановления температуры в зоне реакции до температуры 490–530 °С.
К основным технологическим параметрам рассматриваемой печи, которые регулируются и влияют на процесс, относятся:
– Загрузка в м3/час (вход и выход – 60...80);
– Температура в °С (на входе – 433...443, на выходе – 500...530);
– Давление в кг/см2 (24...28).
В результате анализа доступных данных и исследования режимов работы этих агрегатов (см. табл. 2.1) для разработки моделей этих агрегатов выбраны экспериментально-статистические методы построения моделей.
Математическое описание, являющееся основой модели, должно раскрывать взаимосвязи параметров тепловой работы печи. В составе математического описания тепловой работы печи можно выделить следующие три группы соотношений:
1. Уравнения, описывающие процессы тепломассобмена (уравнения теплопроводности, уравнения лучистого и конвективного теплообмена, уравнения теплового баланса и др.).
2. Теоретические и эмпирические зависимости (зависимости теплофизических характеристик материалов от температуры, температурная зависимость энтальпий паров и жидкостей и др.).
3. Ограничения на режимные параметры, которые задаются в виде равенств или неравенств (расходы топлива, загрузки и др.).
Главный недостаток ранее существовавших методов расчета печей заключается в том, что они ориентированы на оценку лишь интегральных характеристик теплообмена, которые не исключают случая прогара труб. В последнее время на основе теоретического исследования разработан метод моделирования, позволяющий оценить локальные характеристики теплообмена. В математическом отношении сущность зональных методов расчета заключается в замене интегрально-дифференциальных уравнений, описывающих теплообмен, аппроксимирующей конечной системой алгебраических уравнений, из решения которой определяются энергетические характеристики теплообмена – температуры и результирующие потоки отдельных зон системы. С этой целью рассматриваемая печь разбивается на конечное число поверхностных и объемных зон с однородными радиационными свойствами. Этот подход обеспечивает более точный результат расчета (с увеличением числа зон), но сложный и требует данных, которые в промышленных условиях обычно труднодоступны. В то же время для моделирования работы промышленных печей в диалоговом режиме и оперативного получения информации необходимо располагать достаточно простой математической моделью. Поэтому в данной работе в основу разработанного моделирующего алгоритма положен аналитический метод Н.И. Белоконя [132], основанный на совместном решении уравнений теплового баланса
и теплопередачи.
Для расчета выходных параметров печи на основе статистических и экспериментальных данных в модель включены регрессионные уравнения. При этом принято предположение, что вид закона распределения случайных измерения εj близко к нормальному, т.е.:
М[εj] = O, D[εj] = G2 = const, 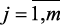 .
.
Тогда структура регрессионных моделей, определяющих объем (у1) и температуру выходного потока (у2) печи П-1 имеет вид:
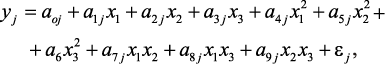 j = 1,2, (2.18)
j = 1,2, (2.18)
где аij (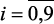 ;
; 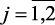 ) – коэффициенты регрессии, идентифицируемые методом наименьших квадратов, х1, х2, х3 – независимые управляющие параметры, соответственно входной поток, температура и давление в печи.
) – коэффициенты регрессии, идентифицируемые методом наименьших квадратов, х1, х2, х3 – независимые управляющие параметры, соответственно входной поток, температура и давление в печи.
В результате обработки данных режимных листов и других статистических данных методами регрессионного анализа и применяя рассмотренную выше программу REGRESS идентифицированы параметры моделей (2.18):
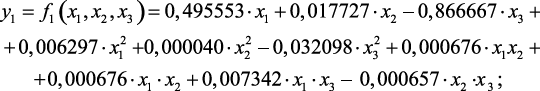 (2,19)
(2,19)
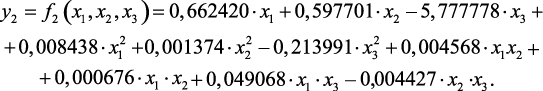 (2,20)
(2,20)
Для моделирования режимов работы сепараторов, теплообменников и фильтров риформинга, можно использовать детерминированные и статистические подходы [11, 133,].
