Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Курмангазиева Л. Т., Оразбаев Б. Б.,
3.2. Разработка диалоговых алгоритмов решения многокритериальных задач оптимизации при управлении технологическим комплексом на основе лингвистического подхода
В данном подразделе предложим набор алгоритмов решения задач многокритериальных задач оптимизации, постановки которые полученных нами в подразделе 3.1. Разработанные методы основываются на идее различных компромиссных схем (методы главного критерия и идеальной точки, принципы Парето оптимальности, равенства и др.) принятия решений, модифицированных и работоспособных на основе качественной информации (в нечеткой среде).
Для решения задачи (3.3)–(3.4) предложим модифицированные методы главного критерия и максимина. Здесь ЛПР выбирается (определяется) главный критерий, который оптимизируется при ПР, а остальные критерии вводятся в систему ограничений, предварительно, с помощью ЛПР, определяются граничные значения этих критериев. Степень выполнения нечетких ограничений учитывается с помощью функций принадлежности mq(x),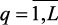 
, а важность каждого из ограничений учитывается на основе определяемых ЛПР весового вектора bq ≥ 0, 
.
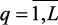Алгоритм решения задачи многокритериальной нечеткой оптимизации (3.3)–(3.4) на основе этого метода состоит из следующих процедур:
Алгоритм ГК-ММ:
1. Задается pq,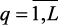 
– число шагов по каждой q-й координате и ряд приоритета для локальных критериев Ik = {1, …, m} (главный критерий должен иметь приоритет 1).
2. ЛПР вводится значение весового вектора ограничений b = (b1, …, bL), учитывающее важность локальных ограничений.
3. ЛПР назначаются граничные значения (ограничения) локальных критериев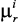 
, 
.
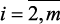4. Определяются hq = 1/pq,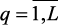 
– величины шагов для изменения координат весового вектора b.
5. Построение набора весовых векторов b1, b2, …, bN, N = (p1 + 1)(p1 + 1)…(pL + 1), варьированием координат на отрезках [0, 1] с шагом hq.
6. Определяется терм-множества Т(Х, У), описывающие качественные (нечеткие) параметры объекта и процесса.
7. Строятся функции принадлежности выполнения нечетких ограничений mq(x),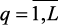 
.
8. Максимизируется главный критерий (3.3) на множестве Х, определяемом по принципу максимина (3.4) и находятся решения: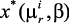 
, 
, …, 
; 
, …, 
, 
.
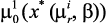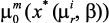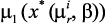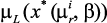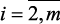9. Решение предъявляется ЛПР. Если текущие результаты не удовлетворяют ЛПР, то им назначаются новые значения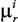 
), 
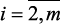и (или) корректируются значения весового вектора ограничений b, осуществляется возврат к пункту 3. Иначе, перейти к пункту 8.
10. Поиск решения прекращается, выводятся результаты окончательного выбора ЛПР: значения вектора управления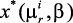 
; значения локальных критериев 
, …, 
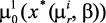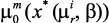и степень выполнения ограничений 
, …, 
.
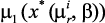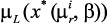Для решения многокритериальной задачи нечеткой оптимизации (3.5)–(3.6) в данной работе предложен следующий метод, разработанный на основе модификации компромиссных схем Парето оптимальности и идеальной точки [127]. Алгоритмизация разработанного метода имеет следующую структуру:
Алгоритм ПО-ИТ:
1. На основе экспертной оценки определить значения весового вектора, оценивающие взаимную важность локальных критериев (целевых функций) g = (g1, …, gm), gi ≥ 0,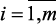 
, g1 + g2 + … + gm = 1.
2. Определяется терм-множества Т(Х, У), описывающие качественные (нечеткие) параметры объекта и процесса.
3. Строятся функции принадлежности выполнения нечетких ограничений mq(x),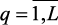 
.
4. Определяются координаты идеальной точки. В качестве координат этих точек можно использовать максимальные значения функции принадлежности: mu = (max m1(x), …, max mL(x) или единицы: mu = (1, …, 1) (если функции принадлежности нормальные).
5. Выбирается вид метрики ||m(x) – mu||D, определяющей расстояние решения x* от идеальной точки – mu.
6. Решить задачу (3.5)–(3.6) и определить решения: оптимальные значения управляющих параметров – x*(g, ||•||D); значения локальных критериев –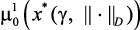 
, 
, …, 
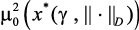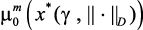и степень выполнения ограничений – m1(x*(g, ||•||D)), …, mL(x*(g, ||•|D)).
7. Предъявить ЛПР полученное решение. Если текущие результаты не удовлетворяют ЛПР, то им назначаются новые значения весового вектора g, и (или) выбирается новый вид метрики ||•||D и поиск приемлемого решения повторяется, иначе процедуру поиска решения прекратить и вывести окончательные результаты.
Для решения задачи (3.7)–(3.8) используя и модифицируя идеи компромиссных схем абсолютной (относительной) уступки и Парато оптимальности разрабатываем следующий алгоритм. К критериям применяется, модифицированный принцип абсолютной или относительной уступки, а для учета выполнения ограничений применяется принцип Парето оптимальности на основе соответствующих функций принадлежности mq(x),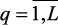 
.
Диалоговый алгоритм решения данной задачи оптимизации состоит из следующих основных пунктов.
Алгоритм А(О)У-ПО:
1. На основе экспертной процедуры определяются значения весового вектора g = (g1, …, gm), Σgi = 1, gi ≥ 0,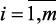 
.
2. В случае нечеткости m0(x), g для них определить терм-множества и построить функции принадлежности.
3. Определяется терм-множество, описывающие качественные параметры и ограничений.
4. Строятся функции принадлежности выполнения ограничений mq(x),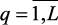 
.
5. ЛПР вводится значение весового вектора ограничений
b = (b1, …, bL), учитывающее важность локальных ограничений.
6. Решается задача максимизации max m0(x),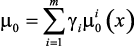 
(в случае абсолютной уступки) или 
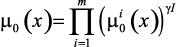, либо 
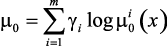(в случае относительной уступки). Определяются решения: оптимальные значения режимных параметров – x*(g, b); оптимальные значения локальных критериев – 
, …, 
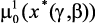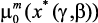и степень выполнения ограничений – m1(x*(g, b)), …, mL (x*(g, b)).
7. Решение предъявляется ЛПР. Если текущие результаты не удовлетворяют ЛПР, то им назначаются новые значения или корректируются значения g и (или) b, и осуществляется возврат к пункту 2. Иначе, перейти к пункту 8.
8. Поиск решения прекращается, выводятся результаты окончательного выбора ЛПР: значения вектора управления x*(g, b); значения локальных критериев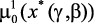 
, …, 
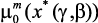и степень выполнения ограничений m1(x*(g, b)), …, mL(x*(g, b)).
Таким образом, разработан набор диалоговых алгоритмов для решения многокритериальных задач оптимизации и выбора оптимальных режимов работы технологических объектов нефтеперерабатывающего производства в условиях неопределенности на примере технологического комплекса блока каталитического риформинга установки ЛГ. Алгоритмы получены непосредственным участием авторов данной работы. Следует отметить, что при решении поставленных задач можно адаптировать и применять алгоритмы предложенные в работах [128, 129, 130], которые использованы при решении задач оптимизации и управления технологическими объектами других
производств.
В приведенных постановках задач многокритериальных оптимизации и разработанных методах их решения реализовалась идея сохранения нечеткости на основе методов компромиссных схем, теории нечетких множеств и возможностей. Предложенные постановки задачи и алгоритмы их решения являются обобщением многокритериальных задач на случай нечеткости исходной информации, они работоспособны и в частных случаях, когда имеется количественная (четкая) информация об исследуемом объекте, что обеспечивает универ-
сальность подхода.