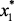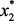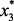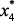Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

РАЗРАБОТКА МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ И ОПТИМИЗАЦИЯ ХИМИКО-ТЕХНОЛОГИЧЕСКИХ СИСТЕМ ПРИ НЕЧЕТКОСТИ ИСХОДНОЙ ИНФОРМАЦИИ

Курмангазиева Л. Т., Оразбаев Б. Б.,

3.4. Постановка и решения задачи оптимизации режимов работы блока каталитического риформинга

В качестве примера сформулируем постановку и приведем решения задачи принятия решения по оптимизации режима работы технологического комплекса блока риформинга установки ЛГ Атырауского НПЗ. Любое производство, вырабатывающее некоторую продукцию (в нашем случае нефтепродукты), будем характеризовать двумя параметрами: объёмом выпускаемой продукции и её качеством. Объём выпуска можно определять различными показателями: валовой, реализованной, чистой нормативной продукцией и т.д. В нашем случае объём выпуска продукции (катализата) измеряется в единицах м3/ч [64–80]. Что касается оценки качества, то здесь дело обстоит не так просто. Оценивать качество выпускаемой продукции одним числом очень трудно и не всегда возможно. В данной задаче качество катализата определяется: октановое число (не менее 86 по моторному методу); фракционный состав – 10 и 50 % отгонка (соответственно не выше 70 и 115 °С); давление насыщенных паров (не более 500 мм рт.ст.); содержание фактических смол в мг. на 100 мл. бензина (не более 5,0). По сути, качественные показатели характеризуются критериями или ограничениями типа «не менее» и «не более», т.е. являются нечеткими.

На практике хочется, чтобы выпуск был побольше, а качество получше. Но, как известно, эти критерии часто являются противоречивыми и улучшать их одновременно часто не удается. Задача заключается в том, чтобы наитий оптимальное решение в области компромиссов, зависящее от производственной ситуации и плана, а также удовлетворяющее ЛПР. Таким образом, используя вышеприведенные постановки задач (см. 3.1) для оптимизации процесса риформинга можно формализовать и ставить следующим образом:

Пусть 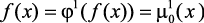– нормализованный критерий, оценивающий выход катализата. Допустим, что для каждого нечеткого ограничения, описывающего качественные показатели продукции 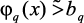, , 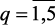построена функция принадлежности его выполнения mq(x) .
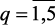Известен либо ряд приоритетов для ограничений Ir = {1, …, 3}, либо весовой вектор, отражающий взаимную важность этих ограничений b = (b1, …, b3).

Как уже отмечалось, критерий и ограничения зависят от вектора параметров xi, 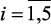(x1 – загрузка сырья; x2, x3 – температура и давление в реакторах Р-4,4а; x4 – объемная скорость подачи сырья; x5 – отношение водород/сырье). Эти зависимости описывают модели, разработанные в предыдущем разделе.

Формализованную задачу, в условиях многокритериальности и нечеткости, можно записать аналогично (3.7)–(3.8) в виде следующей задачи оптимизации:

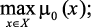(3.9)

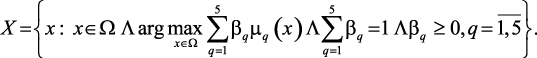(3.10)

Решением данной задачи является значение вектора режимных параметров 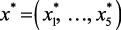, обеспечивающее оптимальное значение критерия при выполнении заданных ограничений, учитывающее предпочтения ЛПР и удовлетворяющее его.

Для решения поставленной задачи (3.9)–(3.10) применяем упрощенную модификацию алгоритма А(О)У-ПО на случай одного критерия.

1. Так как в нашем случае один критерий, его вес равен 1, необходимость определения значения весового вектора g = (g1, …, gm), 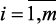отпадает.

2. В поставленной задаче m0(x), четкий, поэтому для него Т(Х, У) и функции принадлежности не строятся.

3. Определяется терм-множество, описывающие нечеткие ограничений. В результате экспертных процедур, ЛПР, специалистов-экспертов для описания ограничения выбраны: не менее 86 по моторному методу; не выше 70 °С; не выше 115 °С; не более 500 мм рт.ст.; не более 5,0 и их производные, которые получаются с помощью различных модификаторов.

4. Строятся функции принадлежности выполнения ограничений mq(x), .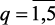

На основе результатов исследований построены следующие функции принадлежности выполнения ограничений:

m1(х) = exp(83,0|у2 – 87)⋅0,78|);

m2(х) = exp(75,0|у3 – 69)⋅0,85|);

m3(х) = exp(120,0|у4 – 114)⋅0,50|);

m2(х) = exp(510,0|у5 – 500)⋅0,25|);

m3(х) = exp(6,50|у6 – 5)⋅1,5|),

где у2, у3, у4, у5, у6 – числовые значения нечетких показателей качества катализата, полученные при использовании множества уровня a в разделе 2; 1 – коэффициенты определяют параметр, который находится при идентификации функции принадлежности и определяющий уровень нечеткости на уровне параметр, который находится при идентификации функции принадлежности и определяющий уровень нечеткости при a = 0,5; 2 – коэффициенты определяют нечеткую переменную, наиболее соответствующую выбранному терму, для которой функция принадлежности принимает максимальное значение (как правило 1); 3 – коэффициенты используются для изменения области определения термов и формы графика функции принадлежности нечетких параметров.

5. ЛПР вводится значение весового вектора ограничений b = (b1, …, b5), учитывающее важность локальных ограничений. В нашей задаче ЛПР ввели следующие значения b1 = 0,7, b2 = b3 = 0,1, b4 = b5 = 0,05, т.е. b = (0,7; 0,1; 0,1; 0,05; 0,05).

6. Решается задача максимизации критерия, т.е. выхода катализата max m0(x) с учетом наложенных нечетких ограничений. Определяются решения: оптимальные значения режимных параметров – x*(b); оптимальное значение критерия – m0(x*(b)) и степень выполнения ограничений – m1(x*(b)), …, m5 (x*(b)).

7. Решение предъявляется ЛПР. Если текущие результаты не удовлетворяют ЛПР, то им назначаются новые значения или корректируются значения b, и осуществляется возврат к пункту 2. Иначе, перейти к пункту 8.

8. Поиск решения прекращается, выводятся результаты окончательного выбора ЛПР: значения вектора управления x*(b); значение критерия m0(x*(b)) и степень выполнения ограничений m1(x*(b)), …, m5 (x*(b)). Эти результаты приведены в виде таблицы (см. табл. 3.1).

Таблица 3.1

Сравнение результатов оптимизации по предложенному алгоритму,
по детерминированному методу [131] и экспериментальных данных

Примечание: ()л означает, что соответствующие качественные показатели определяются лабораторным путем и требуют достаточного времени; (-) означает, что соответствующие показатели не определяются данным методом. Время поиска решения в сравниваемых методах почти одинаково: около одной минуты с учетом времени ввода или корректировки требуемых данных.

Анализ результатов приведенных в табл. 3.1 данных даёт основание сделать следующие выводы:

1. Предложенный алгоритм более эффективно по сравнению детерминированным методом.

2. При решении задач многокритериальных оптимизации на основе предложенного алгоритма, повышается адекватность решения производственной задачи, так как, учитывается дополнительная качественная информация (опыт, знания ЛПР, специалистов-экспертов) более полно описывающая реальную ситуацию без идеализации.

3. Предложенный и использованный алгоритм позволяет определить степень (функцию) принадлежности выполнения того или иного нечеткого ограничения, т.е. степень правильности полученных решений.

Достоверность полученных результатов и выводов подтверждается: корректностью используемых методов исследований, базирующихся на научных положениях теории оптимизации, теорий нечетких множеств и методов экспертных оценок; достаточной сходимостью расчетно-модельных (теоретических) и экспериментальных (опытно-промышленных) результатов исследования (относительная погрешность не более 3 %).
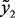
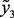
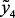
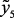
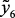
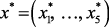