Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.2. Решетчатые функции
В основу метода дискретных преобразований входит понятие о решетчатой функции. Решетчатой функцией называется такая функция, значения которой определены только для дискретных равноотстоящих друг от друга значений независимой переменной, как показано, например, на рис. 1.4, где Т – положительная величина, определяющая расстояние между соседними значениями независимой переменной.
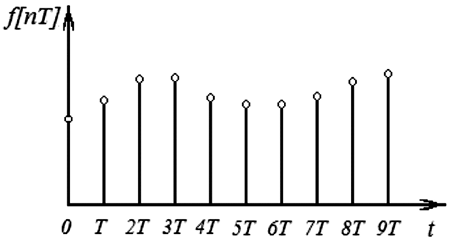
Рис. 1.4. Решетчатая функция f[nT]
Решетчатую функцию можно образовать из непрерывной функции, если для функции f(t) положить t = nT. Например, если имеется непрерывная функция f(t) = eαt, то соответствующая ей решетчатая функция будет иметь вид f[n] = eαnT.
Одной решетчатой функции могут соответствовать несколько непрерывных функций (рис. 1.5), которые называются ее огибающими.
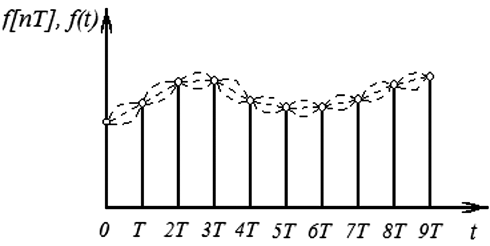
Рис. 1.5. Решетчатая функция и ее огибающие
Решетчатые функции необязательно отражают непрерывные функции. Любую таблицу, составленную из определенных величин через равные интервалы аргумента, можно рассматривать как решетчатую функцию. Так как n есть целое число, обозначающее номер ординаты,
для которой дается значение решетчатой функции, то расстояние между соседними значениями независимой переменной равно единице. Например, для непрерывной функции f(t) = sin ωt при заданном интервале Т решетчатая функция будет иметь вид f[n] = sin ωTn = sin ω1n,
где принято ω1 = ωT.
Решетчатая функция является математической абстракцией реального дискретного сигнала. Дискретный, сигнал (в том числе и импульсный) образуется из непрерывного в результате квантования по времени. На рис. 1.6 показана структурная схема периодического квантователя с конечным временем выборки.
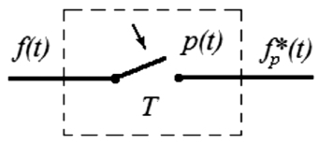
Рис. 1.6. Структурная схема периодического квантователя
с конечным временем выборки Т
Длительность импульса или время выборки равно τ, Т – период квантования. Безусловно, на практике время выборки τ или временной интервал, в течение которого ключ квантователя замкнут, является конечным.
Для входного сигнала f(t), который является функцией непрерывно изменяющегося параметра t, выход квантователя, обозначенный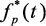 
,
представляет последовательность импульсов конечной длительности, амплитуда которых модулирована входным сигналом (рис. 1.7). Такая модуляция называется амплитудно-импульсной.
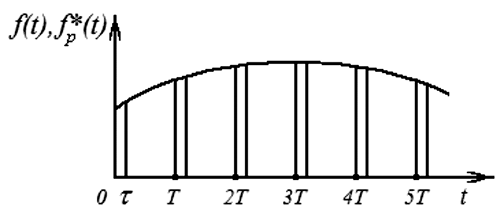
Рис. 1.7. Входной f(t) и выходной 
сигналы квантователя
Для математического описания преобразования непрерывного сигнала f(t) в дискретный удобна следующая математическая модель сигнала
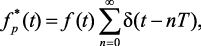(1.23)
которая представляет собой бесконечную последовательность δ-импульсов, модулированных непрерывной функцией f(t) (рис. 1.8) [68]. Звездочкой обычно обращают внимание на сингулярность (одиночность) функции. Эту функцию можно трактовать как результат перемножения функции f(t) и бесконечной последовательности единичных δ-функций.
Из рис. 1.8 следует, будто дельта-функции модулированы по амплитуде. На самом деле это условное обозначение (стрелками) того факта, что дельта-функции модулированы по площади.
Однако дельта-функция, амплитуда и форма импульса, которой не оказывает влияния на реакцию инерционных объектов, не может быть использована в исследовании объекта, минимальная постоянная времени которого соизмерима с периодом дискретизации в численных методах анализа динамических систем. Поэтому в дальнейшем используем формулу (1.23) для представления амплитудно-модулированного сигнала
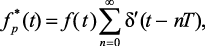(1.24)
где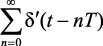 
– бесконечная последовательность δ-импульсов, модулированных непрерывной функцией f(t).
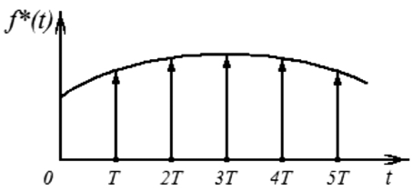
Рис. 1.8. Бесконечная последовательность δ-импульсов, модулированных непрерывной функцией f(t)
Если возникает необходимость использования амплитудно-модулированного сигнала в исследовании инерционных объектов, то
в формулу (1.23) вводится коэффициент Q, показывающий во сколько раз площадь импульса δ′(t) больше единицы:
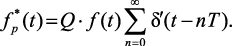(1.25)