Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.3. Составление и решение разностных уравнений
Разности решетчатых функций аналогичны производным непрерывных функций [68]. Первая разность, или разность 1-го порядка, определяется как разность между предыдущей и последующей ординатами решетчатой функции
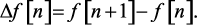(1.26)
Разность 2-го порядка определяется следующим выражением:
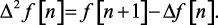(1.27)
Согласно (1.26), имеем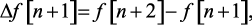 
следовательно,
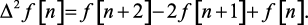(1.28)
Выражение разности 3-го порядка имеет следующий вид
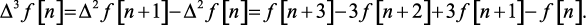(1.29)
Разность k-го порядка определяется по алгоритму, представленному математическим выражением
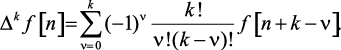(1.30)
Пример 1.1. Решетчатая функция характеризуется выражением f[n] = an2. Определить разность этой функции.
Решение. Первая разность
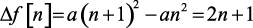
и вторая разность
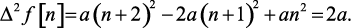
Уравнение, связывающее решетчатую функцию и ее разности с аргументом n, называется разностным уравнением, или уравнением в конечных разностях.
В общем виде неоднородное линейное разностное уравнение с постоянными коэффициентами m-го порядка можно записать в виде:
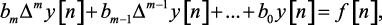(1.31)
где y[n] – искомая функция (реакция); f[n] – заданная функция (возмущение). При f[n] = 0 уравнение (1.31) будет однородным.
Если в разностном уравнении (1.31) разности заменить решетчатыми функциями по формуле (1.30), то получим другой вид разностного уравнения:
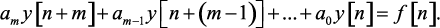(1.32)
Нетрудно установить связь между коэффициентами ak и bk. Например, если дано уравнение
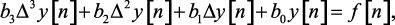
то, подставляя в него значение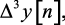 
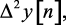
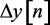из (1.26), (1.27), (1.28), получим
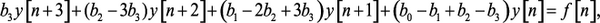
отсюда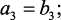 
.
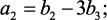
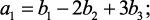
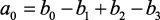Разностное уравнение, записанное в формуле (1.32), можно рассматривать как рекуррентную формулу, позволяющую последовательно вычислять значения y[m], y[m + 1], y[m + 2], ... , если известны y[0], y[1], y[2], ..., y[m – 1]. В этом заключается одно из отличий разностных уравнений от дифференциальных. Другое отличие состоит в том, что порядок разностного уравнения может не совпадать с наивысшим порядком разности.
Для разностного уравнения m-го порядка задаются начальные значения решетчатой функции: либо y[0] и Δky[0] (при k = 1, 2,…, m – 1), если уравнение имеет вид (1.31), либо y[0], y[1], y[2], ..., y[m – 1], если уравнение имеет вид (1.32).
Пример 1.2. Дано разностное уравнение
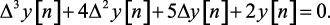
Определить другой вид (1.32) разностного уравнения.
Решение. Заменим разности соответствующими значениями решетчатой функции. В результате выполненной операции получим
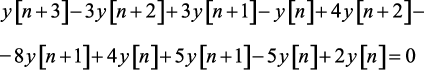
или y[n + 3] + y[n + 2] = 0. После замены n1 = n + 2 это уравнение принимает вид y[n1 + 1] + y[n1] = 0, то есть переходит в однородное разностное уравнение 1-го порядка.
Пример 1.3. Составим временное разностное уравнение для конденсаторного счетчика импульсов (рис. 1.9, а) при uc(0) = 0. На рис. 1.9, б изображена времяимпульсная диаграмма, поясняющая работу счетчика импульсов. Входным напряжением счетчика является импульсный сигнал, представляющий собой последовательность прямоугольных импульсов с амплитудой Um, длительностью τ и периодом следования T. В интервале времени, когда на вход счетчика поступает импульс, происходит заряд конденсатора до некоторого напряжения, которое после окончания действия этого импульса сохраняется до прихода
следующего импульса.
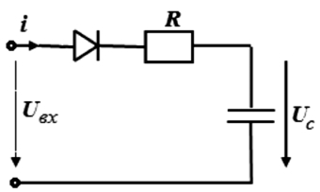
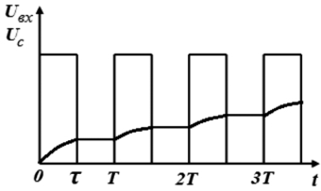
а б
Рис. 1.9. Конденсаторный счетчик импульсов
и его времяимпульсная диаграмма
Решение. В качестве решетчатой функции рассмотрим значения напряжения на конденсаторе в конце периода, которые соответствуют напряжениям при срезах импульсов сигнала uвх(t). Предположим, что в начале n-го интервала напряжение на конденсаторе было равно uc(n). Для удобства анализа введем переменную интервала t, которая изменяется в пределах от нуля до T, а в данном примере она фактически не превышает величины τ.
В интервале действия импульса напряжение на конденсаторе определяется выражением [1]
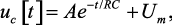(1.33)
где A – коэффициент свободной составляющей uc[t], который определяется из начальных условий; Um – принужденная составляющая uc[t], которая равна амплитуде импульса.
Напряжение на конденсаторе в конце n-го интервала равно
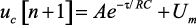(1.34)
или
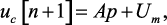(1.35)
где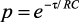 
Определим из начальных условий коэффициент свободной составляющей A, подставив в уравнение (1.34) значения t = 0 и uc[n + 1] = uc[n]:
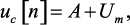(1.36)
откуда
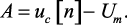(1.37)
Затем подставив выражение (1.37) в уравнение (1.35), получим рекуррентную формулу для вычисления напряжения на конденсаторе
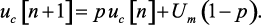(1.38)
Отсюда при начальном условии uc[0] = 0, получим
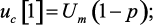
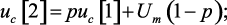
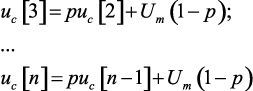
или
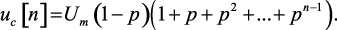(1.39)
Последнее выражение (1.39) представляет собой сумму членов геометрической прогрессии. Следовательно,
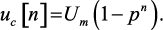(1.40)
Подставляя сюда значение p, получим выражение для напряжения на конденсаторе в начале n-го интервала
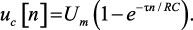(1.41)
Необходимо обратить внимание на то, что в решении (1.41) отсутствует величина периода T, что связано с принципом действия счетчика импульсов, так как в нем происходит только заряд конденсатора в течение времени τ.