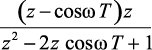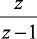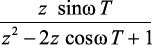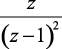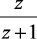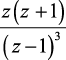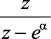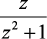Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.4. Прямое z-преобразование
Для решения разностных уравнений используется аппарат z-преобразования, подобно тому, как для решения дифференциальных уравнений применяется преобразование Лапласа.
Определим изображение по Лапласу функции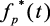 
(1.24):
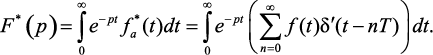(1.42)
Учитывая, что
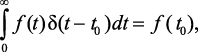(1.43)
а также принимая во внимание, что операции суммирования и интегрирования в (1.42) являются независимыми и очередность их выполнения можно изменить, получим
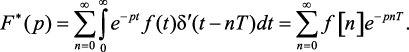(1.44)
Как видно из (1.44), изображение по Лапласу F*(р) содержит оператор р только в виде показательных функций, поэтому, оставаясь в рамках преобразования Лапласа, целесообразно перейти к новой комплексной переменной
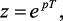(1.45)
определяя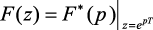 
как z-преобразование решетчатой
функции F(n)
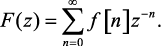(1.46)
Это равенство по аналогии с преобразованием Лапласа дает соответствие между оригиналом f[n] и z-изображением F(z):
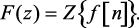(1.47)
Как видно из (1.46), z-изображение представляет собой бесконечный ряд Лорана по степеням z–1, коэффициентами которого являются значения решетчатой функции оригинала в тактовые моменты времени 0, T, 2T, 3T…. Такое представление не всегда удобно, однако из (1.46) вытекает принципиальное свойство z-преобразования: разложив z-изображение F(z) в бесконечный ряд по степеням z–1, можно непосредственно получить тактовые значения оригинала f[n].
Функция F[z] будет существовать в том случае, если ряд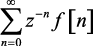 
является сходящимся.
Условие сходимости
Теорема. Достаточным и необходимым критерием сходимости ря-
да (1.46) будет неравенство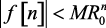 
при 
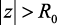[68].
Доказательство. В этом случае
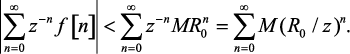(1.48)
Если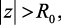 
то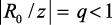 
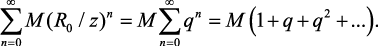(1.49)
Выражение (1.49) представляет собой сумму членов бесконечно убывающей геометрической прогрессии, равную 1/(1 – q).
Следовательно,
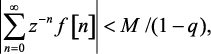(1.50)
где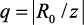 
, то есть ряд сходится вне круга радиуса R0 (рис. 1.10). Теорема доказана.
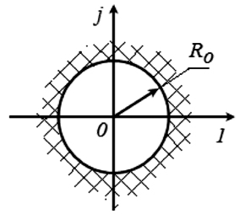
Рис. 1.10. Область сходимости ряда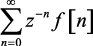 
Наименьшая величина R0, при которой выполняется условие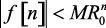 
для любых значений n, называется радиусом сходимости. Если величина R0 конечна, функция f[n] преобразуема.
Для преобразования Лорана так же, как и для непрерывного преобразования, существует ряд сходных теорем [36, 37], доказательства которых приведены далее.
Изображение суммы
Теорема. Если f1[n] и f2[n] имеют z-преобразования f1[z] и f2[z], то
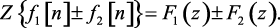
Доказательство. Из определения z-преобразования следует
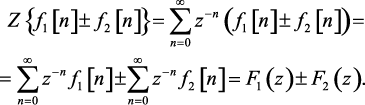(1.51)
Теорема доказана.
Изображение постоянной
Теорема. Изображение постоянной А равно A·z/(z – 1).
Доказательство.
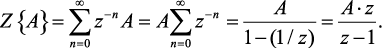(1.52)
При этом радиус сходимости R0 = 1. Теорема доказана.
Теорема запаздывания (сдвига)
Теорема. Если функция f[n] имеет z-преобразование F(z), то
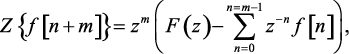(1.53)
где m – положительное целое число.
Доказательство. Найдем изображение функции
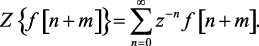(1.54)
Для этого правую часть уравнения (1.54) умножим и разделим на zm
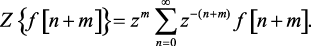(1.55)
Положим n + m = k, тогда
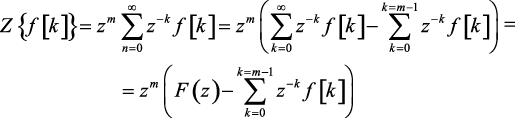
или
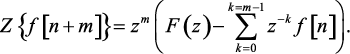(1.56)
Теорема доказана.
Пример 1.4. Пользуясь теоремой запаздывания, определить изображения функции f[n + m] при n = 1, 2, 3.
Решение:
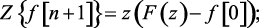(1.57)
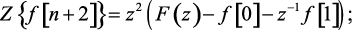(1.58)
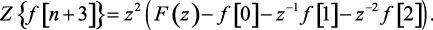(1.59)
Пример 1.5. Найти z-преобразования единичной ступенчатой функции при задержке ее на один период квантования T.
Решение:
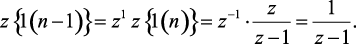(1.60)
Изображение разностей
Теорема. Если функция f(n) имеет z-изображение F(z), то
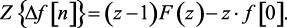
Доказательство. Для разности 
найдем
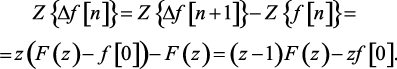(1.61)
Теорема доказана. Подобным путем можно найти изображения для более высоких разностей.
Теорема о свертке во временной области
Теорема. Если функции f1[n] и f2[n] имеют z-преобразования F1(z) и F2(z) и f1[n] = f2[n] = 0 для t = nT < 0, то, то
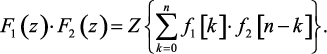(1.62)
Доказательство. Правая часть уравнения (1.62) может быть записана в виде:
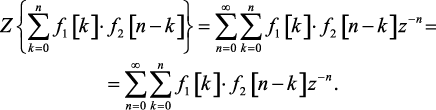(1.63)
Полагая m = n – k и изменяя порядок суммирования, получим
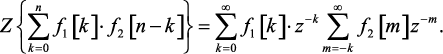(1.64)
Так как f2[m] = 0 при m < 0, то последнее выражение пример вид:
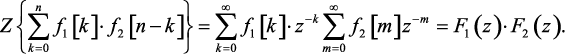(1.65)
Теорема доказана.
Нетрудно заметить, что теорема о свертке во временной области аналогична соответствующей теореме преобразования Лапласа. Однако необходимо помнить, что обратное z-преобразование (или Лапласа) произведения двух функций не равно произведению соответствующих оригиналов.
Теорема о начальном значении
Теорема. Если функция f[n] имеет z-преобразование F(z), и существует предел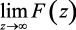 
, то
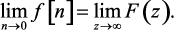(1.66)
Доказательство. По определению F(z) можно представить в виде
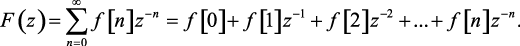(1.67)
Возьмем предел от каждой части последнего выражения и, учитывая, что z стремится к бесконечности, получим
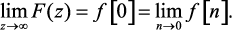(1.68)
Теорема доказана.
Теорема о конечном значении
Теорема. Если функция f[n] имеет z-преобразование F(z) и если функция (1 – z–1)F(z) не имеет полюсов на окружности единичного радиуса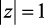 
или вне ее на z-плоскости, то
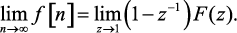(1.69)
Доказательство. Рассмотрим два ряда с конечным числом членов
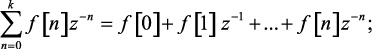(1.70)
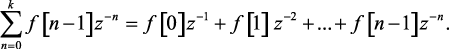(1.71)
Поскольку f[n] = 0 при n < 0, то член f[–1] в выражении (1.71) равен нулю. Из сравнения выражений (1.70) и (1.71) следует, что последний ряд может быть записан в следующем виде:
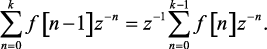(1.72)
Определим в пределе при z → 1 разность между выражения-
ми (1.70) и (1.72):
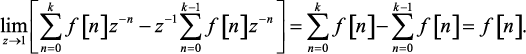(1.73)
В последнем выражении возьмем предел при k → ∞, тогда
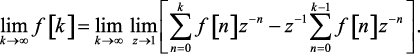(1.74)
Меняя порядок перехода к пределу в последнем выражении, и учитывая, что
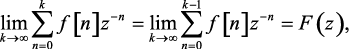(1.75)
получим
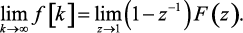(1.76)
Теорема доказана.
С помощью этой теоремы определяется устойчивость решения разностного уравнения: если предел (1.76) имеет конечное число, то решение устойчиво, т.е. ряд не является расходящимся.
Пример 1.6. Используя теорему о конечном значении, определить конечное значение f[n] для заданного z-преобразования:
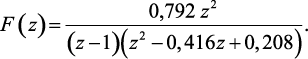(1.77)
Решение. Для решения применяем теорему о конечном значении, так функция
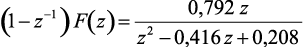(1.78)
не имеет полюсов на единичной окружности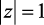 
и вне ее, следовательно, из (1.69) получим
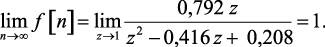(1.79)
Изображения функций [68], наиболее часто применяемых в электротехнике, приведены в табл. 1.1.
Таблица 1.1
Z-изображения некоторых функций
|
Функция |
Изображение |
Функция |
Изображение |
|
f[n] |
F(z) |
cos nTω |
|
|
1[n] |
|
sin nTω |
|
|
n |
|
cos nπ = (–1)n |
|
|
n2 |
|
cos nπ/2 |
|
|
enα |
|
sin nπ/2 |
|
