
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.7. Математическое описание процесса квантования
Для применения аппарата z-преобразования к непрерывным цепям и системам достаточно искусственной дискретизации непрерывного процесса во времени путем введения фиктивного импульсного элемента в соответствующую точку структуры. Тем самым рассматриваемая цепь или система переводится в класс квазидискретных.
При этом существует две возможности выбора места расположения фиктивного импульсного ключа, приводящие к принципиально разным результатам. Если фиктивный ключ располагается непосредственно на выходе интересующей нас величины, то это означает, что процессы в структуре с введением ключа не изменяются. В этом случае мы лишь подвергаем наблюдаемый процесс квантованию во времени, то есть вместо непрерывного сигнала рассматриваем решетчатую функцию, в точности совпадающую с истинным процессом в тактовых точках. От выбора интервала дискретности фиктивного ключа T будет зависеть лишь плотность решетчатой выборки, но не ее точность. Однако, при таком подходе возникают трудности определения корней характеристического полинома, если его степень выше второй.
При расположении фиктивного импульсного элемента на входе или внутри структуры процедура определения z-изображения и оригинала искомой величины упрощается, поскольку в этом случае можно не определять корни характеристического полинома исходной непрерывной системы. Однако описание процесса с помощью решетчатой функции становится приближенным, так как включение фиктивного ключа непосредственно в структуру нарушает ее первоначальный вид.
В связи с этим преобразование Лапласа, удобное для непрерывных сигналов, становится неудобным для дискретных, а удобное для дискретных сигналов z-преобразование – неудобно для непрерывных. Так что проявляется отмеченный еще в апориях элейского философа Зенона факт невозможности непротиворечивого представления непрерывного через дискретное, и наоборот [68].
Выбор интервала дискретизации производится таким образом, чтобы достичь компромисса между повышением точности и чрезмерным увеличением объема вычислений. В большинстве случаев для инженерных расчетов вполне приемлема тактовая частота фиктивного ключа, определяемая с помощью теоремы Котельникова [37], согласно которой частота дискретизации ω1 должна быть в 2 раза больше частотной составляющей ωc сигнала f(t):
ω1 > 2ωc (1.107)
Доказательство. Операция квантования может рассматриваться как преобразование аналогового или непрерывного во времени сигнала в модулированный импульсный сигнал. На рис. 1.6 показана структурная схема периодического квантователя с конечным временем выборки. Длительность импульса или времени выборки равно τ, период квантования – Т.
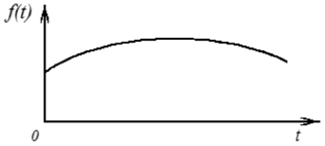
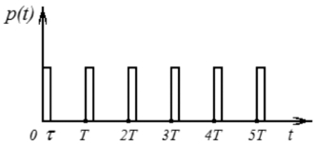
На рис. 1.14 изображены времяимпульсные диаграммы, поясняющие процесс амплитудно-импульсной модуляции входного сигнала f(t). Квантователь, который может быть описан процессом амплитудно-импульсной модуляции, является линейным устройством. Это справедливо, так как квантователь удовлетворяет принципу суперпозиции.
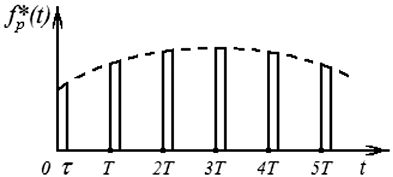
Рассматриваемый здесь квантователь имеет конечную ширину импульсов (рис. 1.14, б), как и в реальных случаях. При рассмотрении процесса выборки можно предположить, что квантователь имеет нулевую длительность импульсов или нулевое время выборки. В этом случае математическое описание квантователя существенно упрощается. Однако для лучшего понимания получаемых результатов сначала рассмотрим общий случай. Несущий сигнал можно выразить как
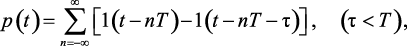 (1.108)
(1.108)
где 1(t) – единичная ступенчатая функция.
В данном случае предполагаем, что операция квантования начинается при t = –∞ и передний фронт импульса совпадает с t = 0. Выход квантователя запишем в виде
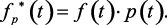 (1.109)
(1.109)
Подставляя соотношение (1.108) в (1.109), получим
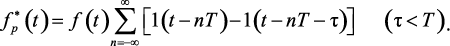 (1.110)
(1.110)
Исследуем частотные характеристики выходного сигнала квантователя. Последовательность импульсов 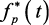 содержит составляющие с большими частотами, чем f(t). Следовательно, квантователь можно рассматривать как генератор гармоник.
содержит составляющие с большими частотами, чем f(t). Следовательно, квантователь можно рассматривать как генератор гармоник.
а б
в
Рис. 1.14. Времяимпульсная диаграмма
амплитудно-импульсной модуляции сигнала f(t)
Поскольку последовательность единичных импульсов p(t) является периодической функцией с периодом Т, то она может быть представлена в виде ряда Фурье
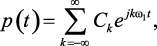 (1.111)
(1.111)
где ω1 = 2π/T – частота квантования; Ck – коэффициенты ряда Фурье в комплексной форме, определяемые как
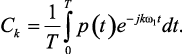 (1.112)
(1.112)
Так как p(t) = 1 для 0 ≤ t ≤ p, то соотношение (1.112) принимает вид
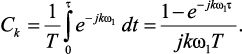 (1.113)
(1.113)
Используя формулу Эйлера, преобразуем выражение (1.113)
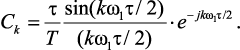 (1.114)
(1.114)
Подставляя соотношение (1.114) в выражение (1.111), имеем
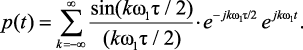 (1.115)
(1.115)
Подстановка p(t) из (1.85) в (1.99) позволяет получить выражение
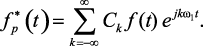 (1.116)
(1.116)
Преобразование Фурье сигнала 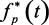 может быть записано в виде
может быть записано в виде
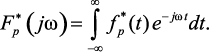 (1.117)
(1.117)
Используя теорему о смещении преобразования Фурье в области комплексной переменной, имеющей математическое выражение
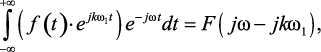 (1.118)
(1.118)
соотношение (1.117) может быть записано как
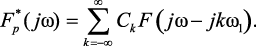 (1.119)
(1.119)
Поскольку k изменяется от –∞ до +∞, то соотношению (1.119) можно придать иную форму
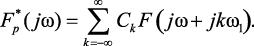 (1.120)
(1.120)
Определим коэффициент ряда Фурье в соотношении (1.104) при k → 0
 (1.121)
(1.121)
В соотношении (1.120) возьмем только член, соответствующий k = 0
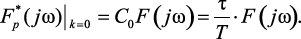 (1.122)
(1.122)
Последнее выражение иллюстрирует важное свойство: гармоники, содержащиеся в непрерывном входном сигнале f(t), представлены и в выходном сигнале квантователя 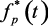 , однако их амплитуды отличаются в τ/T раз.
, однако их амплитуды отличаются в τ/T раз.
Для k ≠ 0 коэффициент Ck является комплексной величиной, но его модуль может быть записан в виде
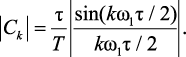 (1.123)
(1.123)
Модуль 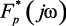 равен
равен
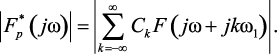 (1.124)
(1.124)
Частотный спектр последовательности единичных импульсов p(t) представляет собой зависимость коэффициентов ряда Фурье Ck в зависимости от ω, когда k принимает различные значения от –∞до +∞. Амплитудный спектр Ck показан на рис. 1.15, а из которого видно, что амплитудный спектр Ck является не непрерывной функцией, а дискретной, представляющей равноотстоящие спектральные линии при ω = kω1.
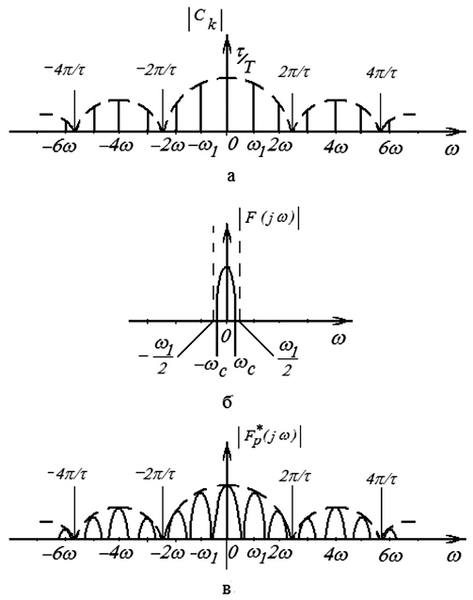
Рис. 1.15. Частотные характеристики сигналов квантователя
Огибающая спектра описывается правой частью соотношения (1.124). Это соотношение можно записать также в форме
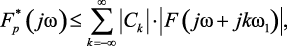 (1.125)
(1.125)
которая может быть использована для иллюстрации амплитудного спектра 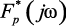 .
.
Предположим, что амплитудный спектр непрерывного входного сигнала имеет форму, показанную на рис. 1.15, б. Тогда на основании соотношения (1.125) спектр 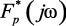 будет иметь вид, показанный на рис. 1.15, в.
будет иметь вид, показанный на рис. 1.15, в.
Следует заметить, что 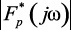 содержат не только основную составляющую F(jω), но и транспонированные составляющие F(jω + jkω1), k = ±1, ±2. Для получения k-й транспонированной составляющей выходного спектра необходимо умножить
содержат не только основную составляющую F(jω), но и транспонированные составляющие F(jω + jkω1), k = ±1, ±2. Для получения k-й транспонированной составляющей выходного спектра необходимо умножить  на соответствующий коэффициент ряда Фурье
на соответствующий коэффициент ряда Фурье 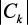 и сдвинуть его на kω1, k = ±1, ±2, ±3 .... Следовательно, квантователь можно представить как генератор гармоник, выход которого содержит основную составляющую и все транспонированные составляющие с соответствующими весовыми коэффициентами, отстоящие друг от друга на частоту квантования. Основная полоса частот передает всю информацию, содержащуюся в непрерывном входном сигнале. Эта же информация повторяется в боковых полосах частот.
и сдвинуть его на kω1, k = ±1, ±2, ±3 .... Следовательно, квантователь можно представить как генератор гармоник, выход которого содержит основную составляющую и все транспонированные составляющие с соответствующими весовыми коэффициентами, отстоящие друг от друга на частоту квантования. Основная полоса частот передает всю информацию, содержащуюся в непрерывном входном сигнале. Эта же информация повторяется в боковых полосах частот.
Частотный спектр 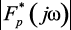 , показанный на рис. 1.15, в, получен при условии, что частота квантователя ω1 превышает более чем в 2 раза высшую частотную составляющую сигнала f(t), то есть ω1 > 2ωc. Если ω1 < 2ωc, то частотный спектр
, показанный на рис. 1.15, в, получен при условии, что частота квантователя ω1 превышает более чем в 2 раза высшую частотную составляющую сигнала f(t), то есть ω1 > 2ωc. Если ω1 < 2ωc, то частотный спектр 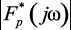 будет искажаться вследствие наложения гармоник и поэтому восстановление исходного сигнала из этого спектра невозможно из-за наложения транспонированных составляющих. Таким образом, частота ω1 должна быть по крайней мере в 2 раза больше высшей частотной составляющей сигнала f(t) – ωc. Теорема
будет искажаться вследствие наложения гармоник и поэтому восстановление исходного сигнала из этого спектра невозможно из-за наложения транспонированных составляющих. Таким образом, частота ω1 должна быть по крайней мере в 2 раза больше высшей частотной составляющей сигнала f(t) – ωc. Теорема
доказана.
