Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.2. Коэффициент линейности преобразования частотных характеристик при цифровом моделировании
При равномерной дискретизации частоты в p-области при точном преобразовании z = epT осуществляется равномерная круговая дискретизация по окружности единичного радиуса на z-плоскости [36, 43]. При цифровом моделировании с использованием различных методов z-форм нарушается равномерность круговой дискретизации (рис. 2.4).
Проведем количественную оценку частотных искажений для каждой z-формы, определив коэффициент линейности по формуле:
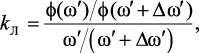(2.19)
где Δω′ – шаг изменения ω′.
Графические зависимости коэффициента линейности от приведенной частоты (Δω = 0,01) для различных методов аппроксимации представлены на рис. 2.5. Номеру графика соответствуют следующие значения приведенного коэффициента затухания: 1 –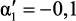 
; 2 –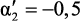 
;
3 –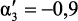 
.
Коэффициент линейности позволяет количественно оценить искажение частотных характеристик, вносимых каждой z-формой, и проводить их сравнительный анализ, который позволяет обоснованно для каждого частотного диапазона выбирать соответствующую форму моделирования цифровых фильтров.
Из проведенного анализа следует, что наименьшие искажения в широком диапазоне частот при отображении области p-полюсов на z-плоскость вносят метод обратной разности и метод трапеций. Там, где предъявляются высокие требования к качеству обработки сигналов целесообразно применять данные методы моделирования.
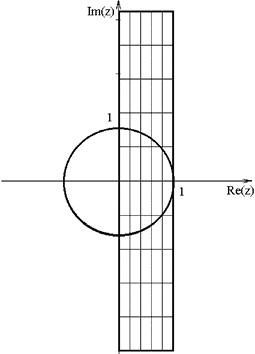
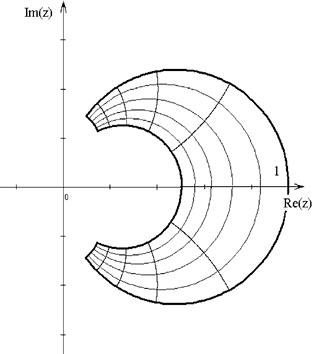
а б
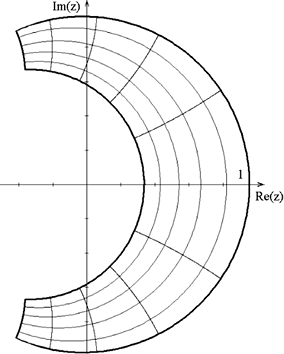
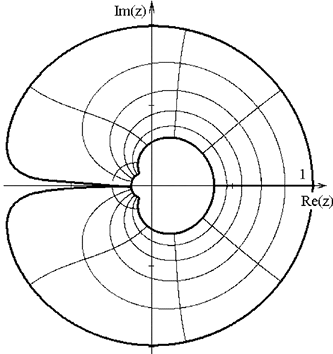
в г
Рис. 2.4. Частотные искажения при трансформации области устойчивости p-плоскости на z-плоскость с помощью методов:
а – прямой разности; б – обратной разности; в – Тустена;
г – преобразования без потерь
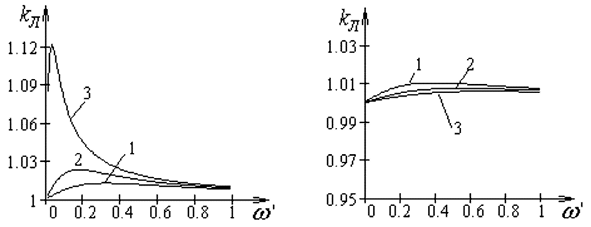
а б
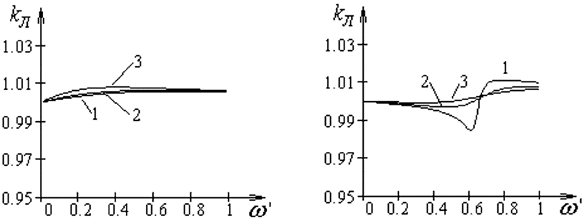
в г
Рис. 2.5. Зависимости kл = f(ω′), полученные с помощью методов:
а – прямой разности; б – обратной разности; в – Тустена;
г – преобразования без потерь