
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.1. Моделирование переходных процессов в линейных звеньях с помощью операторно-дискретного метода
Наиболее распространенными моделями электротехнических и электронных устройств являются схемы замещения. Рассмотрим методику применения операторно-дискретного метода для анализа переходных процессов в линейных электрических звеньях с ненулевыми начальными условиями [94].
Для проведения исследований выберем электрическую схему (рис. 4.1) с источником ЭДС E = 10 В и параметрами: R1 = R2 = 1 кОм; L = 10 мГн; С = 0,1 мкФ. В качестве искомой функции определим закон изменения тока i(t) в цепи после коммутации.
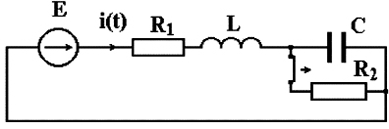
Рис. 4.1. Электрическая схема с ненулевыми начальными условиями
Методика моделирования
Составим дискретную схему замещения цепи после коммутации (рис. 4.2). Значения тока и напряжения на элементах цепи до коммутации: i(0) = E/(R1 + R2) = 5 мА; uC(0) = i(0); R2 = 5 В.
Выберем период дискретизации. Для этого необходима ориентировочная информация о динамических свойствах описываемого уравнением объекта. Из классического метода решения данной задачи известны постоянные времени
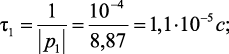
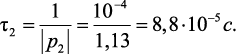
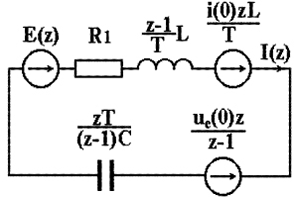
Рис. 4.2. Дискретная схема замещения
электрической цепи после коммутации
Из проведенных экспериментальных исследований влияния периода дискретизации на точность численного метода следует, что согласно требованиям инженерно-технических расчетов, период дискретизации должен быть на два порядка меньше минимальной постоянной времени цепи [76]. В качестве опорной величины при выборе периода дискретизации используем минимальную постоянную времени τ1: T = τ1/100 = 1,1·10–7 c.
Получим z-изображение искомой функции. Согласно закону Ома в дискретной форме z-изображение тока в цепи имеет вид:
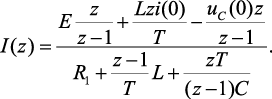 (4.1)
(4.1)
Выполнив математические преобразования в выражении (4.1) получим
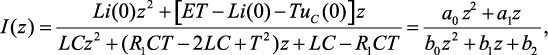 (4.2)
(4.2)
где a0 = Li(0); a1 = ET – Li(0) – TuC(0); b0 = LC; b1 = R1CT – 2LC + T2; b2 = LC – R1CT. Подставив численные значения параметров в выражение (4.2), получим дискретное изображение искомого тока:
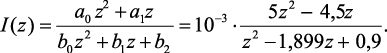 (4.3)
(4.3)
Если при моделировании используется выражение передаточной функции системы, то информация о постоянных времени может быть получена по корням знаменателя.
Определим значения функции оригинала в тактовые моменты времени. Для этого воспользуемся выражениями, полученные из алгоритма деления полиномов числителя и знаменателя z-изображения (1.102), (1.103):
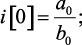
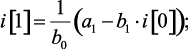
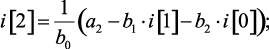
при n > 2
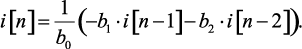 (4.4)
(4.4)
График i[n] приведён на рис. 4.3. Во избежание быстрого накопления погрешности необходимо проводить вычисления с большим количеством значащих цифр, округляя результат до требуемой точности лишь по окончании расчета. В процессе вычислений значений оригинала функции, особенно при сравнительно малых значениях периода дискретизации, накапливается большое количество результатов, что вызывает неудобства с их печатью и регистрацией. Поэтому в программе для вычисления значений i[n] целесообразно регистрировать не все значения, а только кратные некоторому числу.
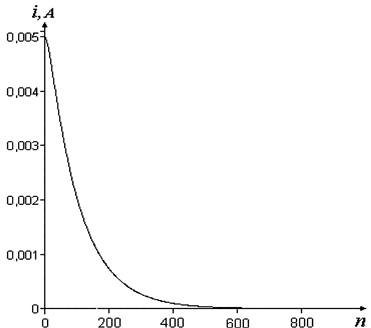
Рис. 4.3. График переходного процесса в цепи, полученный
с помощью операторно-дискретного метода
Вывод. Вычислительный алгоритм операторно-дискретного метода позволяет просто и гибко вычислять реакцию электрических цепей на различные возмущающие воздействия с помощью компьютера, что обусловлено следующими особенностями метода:
– топология схем замещения данного метода полностью совпадает с топологией электрических схем;
– разностные уравнения довольно просто могут быть получены непосредственно из электрических схем без промежуточных операций составления непрерывных уравнений состояния и их дискретизации;
– возможность управления точностью расчета в процессе вычисления за счет изменения периода дискретизации.
