Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.2. Цифровое моделирование линейных элементов методом z-форм
При расчетах переходных процессов различные электротехнические устройства (трансформаторы, асинхронные и синхронные двигатели, освещение, теплоэнергонагреватели, синхронные компенсаторы и др.) представляются в виде линеаризованных моделей – электрических схем замещения. Методика цифрового моделирования линейного блока с помощью операторно-дискретного метода была рассмотрена в раз-
деле 4.1. Рассмотрим методику моделирования, основанную на применении z-форм. Для выбора периода дискретизации воспользуемся результатами исследований, проведенных в главах 2 и 3 [89].
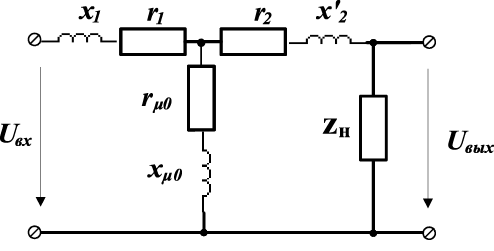
Рис. 4.4. Схема замещения двухобмоточного трансформатора
В качестве объекта исследования рассмотрим двухобмоточный трансформатор, который в системе электроснабжения представляется Г- или Т-образными схемами замещения. Для Т-образной схемы
с параметрами r1 = 50 Ом, x1 = 31,4, r2’ = 50 Ом, x2’ = 31,4 Ом, rμ0 = 1000 Ом, xμ0 = 314 Ом, zн = rн = 500 Ом рассмотрим последовательность расчета импульсной характеристики (рис. 4.4). Анализ переходных процессов проведем операторным методом расчета без учета нелинейности характеристик.
Методика моделирования
Составим операторную схему замещения трансформатора (рис. 4.5).
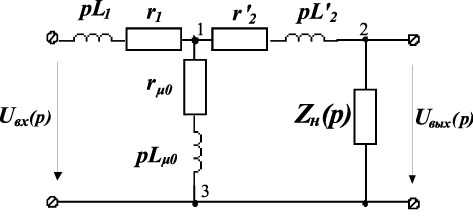
Рис. 4.5. Операторная схема замещения трансформатора
Определим передаточную функцию. С помощью метода узловых потенциалов для схемы на рис. 4.5 составим уравнения в операторной форме:
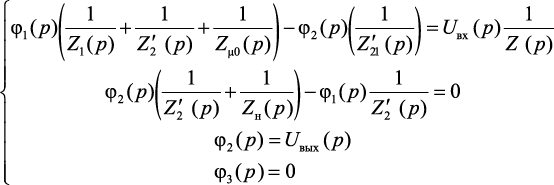(4.5)
где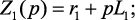 
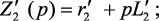
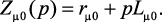
Из системы уравнений (4.5) получим выражение передаточной функции:
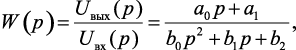(4.6)
где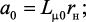 
.
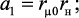
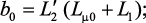
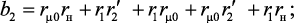
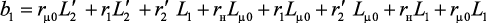Выберем z-форму. Воспользуемся результатами анализа конформных преобразований областей устойчивости p-плоскости на z-плоскость. Для апериодического звена полюса аналоговой передаточной функции трансформируются на положительную полуось Re(z) с помощью рассмотренных способов аппроксимации и не выходят за границу круга единичного радиуса, следовательно, при численном моделировании можно использовать любую из указанных способов аппроксимации, а точностью можно управлять изменением периода дискретизации.
Определим период дискретизации Т. Для передаточной функции динамического звена второго порядка (0 < ξ < 1) в главах 2 и 3 проведены исследования влияния параметров численной модели на устойчивость и погрешность моделирования. Необходимо отметить, что форма представления динамического звена второго порядка соответствует колебательному режиму, который является неблагоприятным для численного моделирования. Эта форма представления может быть использована и для анализа звеньев при апериодическом режиме. В этом случае по постоянным времени двух апериодических процессов Т1 и Т2, которые определяются по коэффициентам выражения (4.6), вычисляются параметры Т0, ξ. Согласно методике выбора относительного периода дискретизации (раздел 3.3) для заданных значений δпр, Δz = 0,001 и формы аппроксимации – обратной разности, получены диапазон относительного периода дискретизации 1,227∙10–3 ≤ с ≤ 1,176∙10–1 и значения погрешностей, соответствующие каждому значению с. Так, например, значению δпр = 0.1 соответствует с = 3,179∙10–2. Необходимо отметить, что погрешность может быть задана и в относительной форме.
Перейдем от непрерывной передаточной функции к дискретной. Используя метод обратной разности, получим передаточную функцию в дискретной форме:
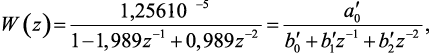(4.7)
где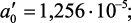 
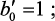
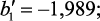b′ = 0,989.
Определим значения импульсной функции в тактовые моменты времени. В формуле (1.105) осуществляется дискретизация входного воздействия. В нашем случае таким воздействием является функция Дирака (δ-импульс), которая определяется следующим образом:
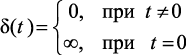(4.8)
при этом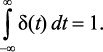 
В качестве входного воздействия рассмотрим реальный импульс прямоугольной формы, длительность которого равна периоду дискретизации Т, амплитуда – 1/T. При этом площадь данного импульса равна единице, то есть условие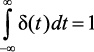 
выполняется.
Алгоритм вычисления значений импульсной функции k(n) в тактовые моменты времени:
……………………………….
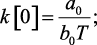
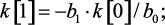
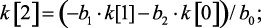
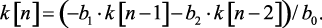(4.9)
График импульсной характеристики k[n] приведён на рис. 4.6.
Метод z-форм позволяет сравнительно просто по непрерывной передаточной функции получить импульсную передаточную функцию. Кроме того, показана методика определения импульсной характеристики с помощью рекуррентной формулы с учетом реального воздействия – прямоугольного импульса. Эти операции легко реализуется с помощью существующих пакетов математических программ.
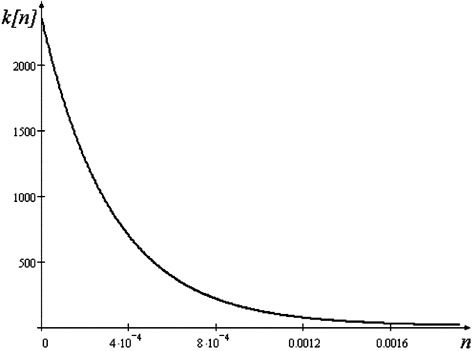
Рис. 4.6. Импульсная характеристика трансформатора