Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.3. Моделирование аналоговых и синтез цифровых регуляторов
Основными типами регуляторов, используемых в промышленности, являются структуры 1-го и 2-го порядков, а именно: ПИ-, ПД- и ПИД-регуляторы. Эти регуляторы могут быть реализованы только в виде цифровых фильтров с бесконечной импульсной характеристикой и рекурсивной структурой. Также следует отметить, что в аналоговых системах управления используются типовые регуляторы, выполненные на базе операционных усилителей. Получение передаточной функции существующего настроенного регулятора не является трудоемкой задачей, и может быть выполнено на основе анализа принципиальной схемы.
Синтез эквивалентного цифрового регулятора может быть осуществлен на основе передаточной функции имеющегося аналогового регулятора. По передаточной функции цифрового фильтра (регулятора) W(z) может быть получено разностное уравнение и структура цифрового фильтра, причем без дополнительных вычислений. На рис. 4.7, 4.8 приведены два основных типа структуры цифровых фильтров (регуляторов). Эти структуры получены по импульсным передаточным функциям, где блок с обозначением z–1 – блок задержки на один такт или устройство выборки и хранения, блоки ai и bj выполняют операции умножения на эти коэффициенты, блок с обозначением + выполняет функцию суммирования [3, 46].
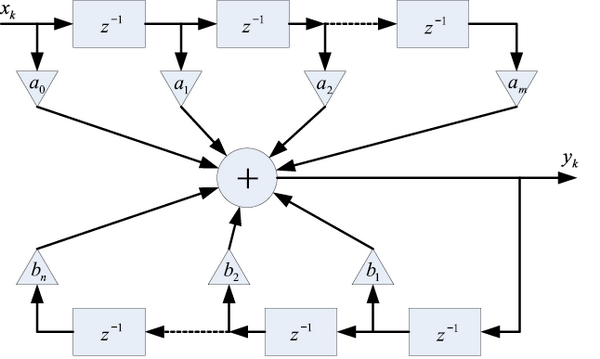
Рис. 4.7. Цифровой фильтр с рекурсивной структурой
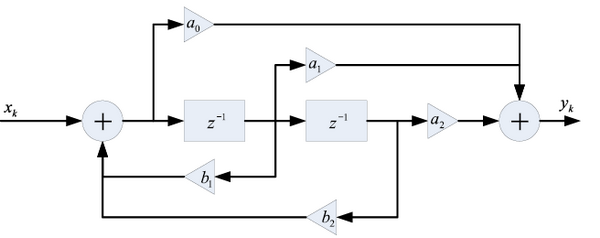
Рис. 4.8. Цифровой фильтр с канонической структурой
Переход от аналоговых устройств регулирования, моделями которых являются схемы замещения, к цифровым устройствам является весьма актуальной задачей, которая решается при модернизации и проектировании электротехнических систем.
4.3.1. Анализ аналоговых регуляторов
Рассмотрим методику цифрового моделирования регулятора, выполненного на базе идеального операционного усилителя (рис. 4.9) для следующих значений проводимостей ветвей:
Y1 = G1 = 0,01 См; Y2 = G2 = 0,002 См; Y3 = pC3 = 10–4p См; Y4 = G4 = 0,05 См; Y5 = pC5 = 10–6p См [79].
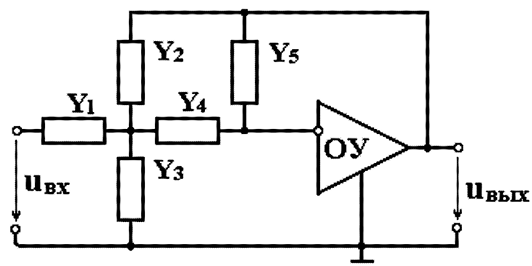
Рис. 4.9. Схема регулятора на операционном усилителе
По передаточной функции аналогового регулятора с помощью метода z-форм получим выражение дискретной передаточной функции, по которому без дополнительных вычислений получим разностное уравнение, совпадающее со структурой цифрового фильтра.
Методика моделирования
Составим эквивалентную схему замещения регулятора (рис. 4.10).
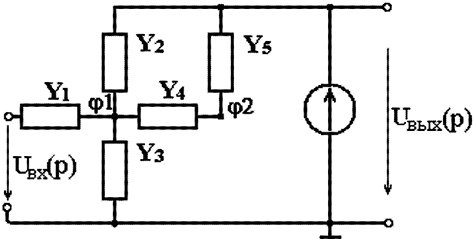
Рис. 4.10. Схема замещения регулятора
Определим непрерывную передаточную функцию регулятора. Для этого воспользуемся системой уравнений, составленной по методу узловых потенциалов:
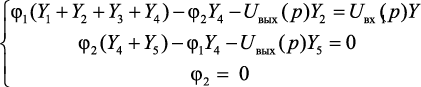(4.10)
Из выражения (4.10) получим передаточную функцию по напряжению:
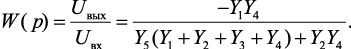(4.11)
Подставляя в выражение (4.11) значения параметров элементов приведем выражение передаточной функции к виду (2.24)
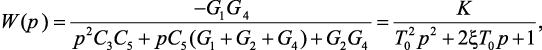(4.12)
где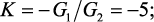 
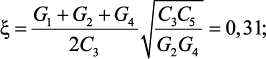
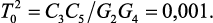
Выберем форму аппроксимации и период дискретизации. Согласно проведенным исследованиям конформных преобразований областей устойчивости в главе 2 следует, что для численного моделирования целесообразно использовать метод обратной разности или метод трапеций. Проверим возможность применения метода прямой разности для решения данной задачи. Согласно методике выбора периода дискретизации, предложенной в разделе 3.3 для выбранного значения ширины области вблизи границы устойчивости Δz = 0,0001 получим диапазон периода дискретизации 3,227∙10–7 ≤ Т ≤ 6,176∙10-4 с и соответствующие значения погрешностей для каждого значения Т. С помощью компьютерной программы получено, что в этом диапазоне Т относительная погрешность моделирования составляет не менее 8 %, поэтому использовать метод прямой разности для данной задачи не целесообразно. Для дальнейших расчетов выберем форму аппроксимации согласно методу трапеций. Согласно методике выбора периода дискретизации, предложенной в разделе 3.3 при Т = 0,0004 с максимальная погрешность моделирования составляет 2 %.
Перейдем к дискретной передаточной функции. Путем замены оператора p в выражении (4.12) согласно выбранной z-формы получим:
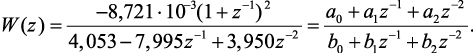(4.13)
Получим алгоритм вычисления значений переходной характеристики в тактовые моменты времени. По выражению дискретной передаточной функции с помощью с помощью разностного уравнения (1.105):
……………………………….
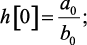
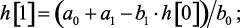
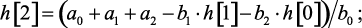
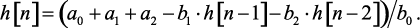(4.14)
График переходной характеристики h[n] приведён на рис. 4.11.
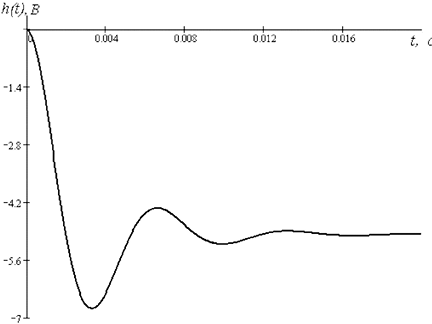
Рис. 4.11. Переходная характеристика регулятора
4.3.2. Синтез цифровых регуляторов по аналоговым моделям
Рассмотрим методику синтеза цифрового регулятора по аналоговой передаточной функции на примере звена второго порядка. Для этого с помощью различных z-форм (прямая разность, обратная разность, метод трапеций) осуществляется переход от аналоговой передаточной функции к импульсной
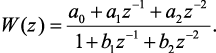
Этому динамическому звену соответствует диаграмма состояния (рис. 4.12, а), которая является графическим отображением причинно-следственных связей между дискретными переменными состояния. Диаграмма может служить основой программы для ЭВМ, при этом ветви с коэффициентами передачи z–1 реализуются временной задержкой на Т секунд.
Переход от изображения к оригиналу функции – уравнениям состояния может быть выполнен по диаграмме состояния (рис. 4.12, б), которая получена после исключения блоков задержки z–1 из диаграммы состояния (рис. 4.12, а). На основе диаграммы состояния и применения формулы Мезона запишем уравнения состояния звена второго порядка:
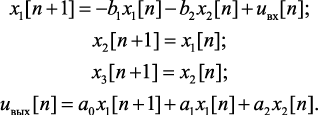
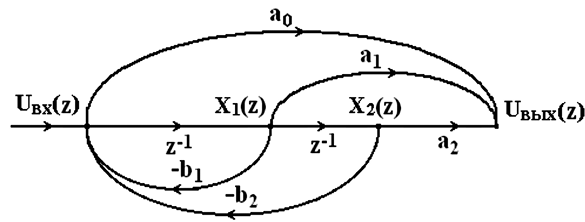
а
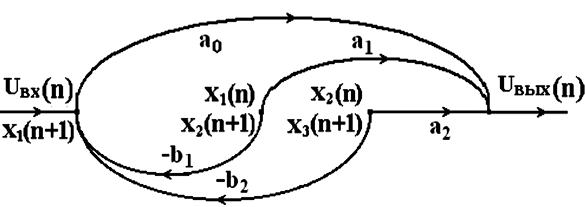
б
Рис. 4.12. Диаграммы состояния динамического звена второго порядка
Диаграмме состояния звена (рис. 4.12, а) соответствует структурная схема цифрового регулятора (рис. 4.13).
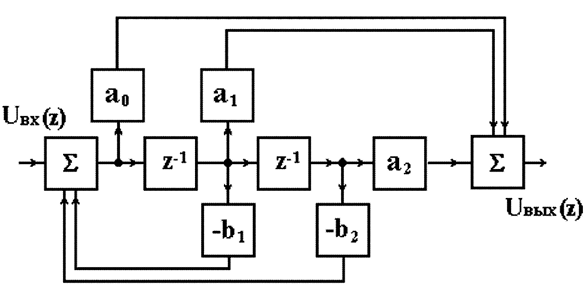
Рис. 4.13. Структурная схема цифрового регулятора
Для автоматизации процесса синтеза цифровых регуляторов была разработана компьютерная программа, которая позволяет построить цифровой регулятор эквивалентный заданному аналоговому регулятору [57]. В программе предусмотрена возможность задать параметры типового регулятора, либо задать передаточную функцию произвольного регулятора. Разработанная программа автоматически, по заданным параметрам аналогового регулятора создает структуру эквивалентного цифрового регулятора, и вычисляет коэффициенты. Таким образом, программа позволяет автоматизировать процесс перехода от аналоговых систем управления к цифровым системам.