Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.5. Цифровое моделирование линии с распределенными параметрами
Одной из сложных задач энергетики является моделирование переходных процессов в линиях электропередачи, которые можно рассматривать, как длинные линии с распределенными параметрами, поскольку сами линии вносят существенный вклад в динамические свойства системы. Нормальные и переходные режимы электропередач характеризуются особенностями, которые обусловлены волновым характером распределения электромагнитной энергии и соотношением удельных параметров линии. Одним из средств, упрощающих представление о процессах, протекающих в энергетической системе, являются схемы замещения линии электропередачи, которые могут быть справедливы при исследовании установившегося или квазиустановившегося режима, или могут отражать связь между параметрами системы и параметрами режима только в определенный момент времени. В зависимости от требуемой точности эти модели представляются в виде различных электрических схем, которые значительно упрощают задачу и вносят погрешность в динамическую модель системы. Упрощение схемы может привести к неверным выводам об устойчивости системы.
К первичным параметрам двухпроводной длинной линии, взятым на единицу длинны линии, относятся: С0 – поперечная емкость между прямыми и обратными проводами; L0 – индуктивность петли, образованной прямыми обратным проводами; R0 – продольное активное сопротивление прямого и обратного проводов; G0 – поперечная активная проводимость утечки изоляции между прямым и обратным проводами. Для расчета этих параметров необходимы исходные данные: номинальное напряжение линии, количество цепей линии, марка и сечение провода, расположение проводов на опоре и расстояние между проводами.
К вторичным параметрам в операторной форме относятся волновое сопротивление:
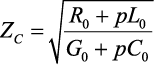(4.23)
и коэффициент распространения:
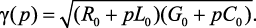(4.24)
Наиболее распространенная схема замещения бесконечно малого элемента двухпроводной линии показана на рис. 4.18 [7].
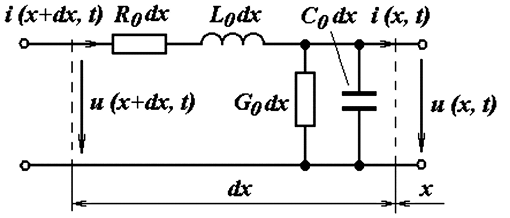
Рис. 4.18. Схема замещения элементарного участка линии
Анализ установившихся и переходных режимов в однородных длинных линиях ведется на основе дифференциальных уравнений в частных производных, полученных с помощью законов Кирхгофа для элемента линии длиной dx (рис. 4.18):
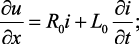(4.25а)
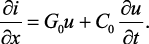(4.25б)
Необходимо отметить, что уравнения (4.25) имеют аналитическое решение для частного случая, а именно при гармонических воздействиях, однако для анализа переходных процессов целесообразно определение переходных функций, поскольку единичное ступенчатое воздействие содержит гармонические составляющие всех частот. В литературных источниках представлены аналитические решения этой задачи для частных случаев, а для общего случая используются численные методы расчета и разработанные на их основе программы. При использовании численных методов точность моделирования ограничена, причем оценить ее сложно [26, 31].
При синусоидальном напряжении источника питания однородной линии и постоянных параметрах уравнения (4.25) записываются в комплексной форме:
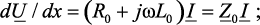(4.26а)
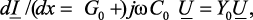(4.26б)
где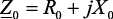 
Ом/м;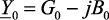 
См/м – комплексные продольные и поперечные параметры линии на единицу длины.
Общее решение уравнений (4.26) представляет собой сумму прямых и обратных бегущих волн с напряжением и током:
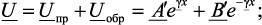(4.27а)
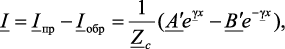(4.27б)
где А’, В’ – постоянные интегрирования; Zc – характеристическое сопротивление. Постоянные интегрирования определяются с использованием граничных значений тока и напряжения при х = 0 (х – расстояние от конца линии).
Цепь с распределенными параметрами также рассматривают как четырехполюсник, гармонические режимы в котором описываются уравнениями в А-параметрах. Если заданы напряжения U2 и ток I2 в конце линии, то можно определить напряжения U1 и ток I1 в начале линии:
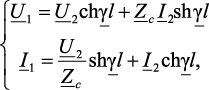(4.28)
где Z2 – сопротивление нагрузки линии.
Однородную длинную линию можно заменить эквивалентной цепной схемой, разделив линию длинной l на N одинаковых отрезков
каждый из которых имеет длину l0 = l/N (рис. 4.19). Масштаб квантования (l0 – длина одного звена) определяется необходимой точностью моделирования линии при помощи цепной схемы. Каждый из отрезков линии можно заменить эквивалентным четырехполюсником.
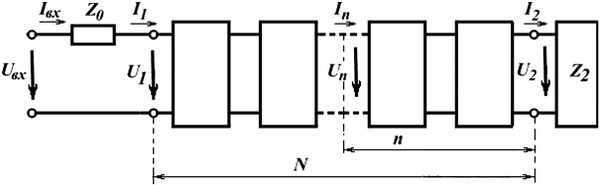
Рис. 4.19. Эквивалентная цепная схема
Для промежуточного n-го звена однородной цепной схемы напряжения и токи на его входе определяются следующим образом [31]:
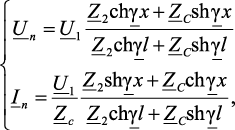(4.29)
где х = l0n – расстояние от конца линии.
Из выражений (4.29) получено выражение передаточной функции по напряжению однородной цепной схемы [31]:
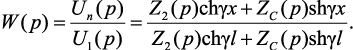(4.30)
Это выражение сравнительно сложно для существующих методов анализа переходных процессов и устойчивости системы, поскольку данные методы используют передаточные функции в виде дробно-рационального выражения, а передаточная функция линии содержит гиперболические функции. Однако при дискретизации передаточной функции гиперболические функции можно выразить через экспоненциальные, а экспоненциальные функции могут быть преобразованы без потери точности в область z переменной. Такое моделирование позволяет получить более точную и удобную модель для реализации цифровых систем.
В практике инженерных расчетов каждая фаза линии электропередач представляются в виде четырехполюсника, который в свою очередь заменяется простой схемой электрической цепи с сосредоточенными параметрами. В уравнениях четырехполюсника при небольшой длине линии делается допущение, что гиперболические функции приближенно равны своим аргументам. Следует отметить, что представление линии упрощенными схемами замещения позволяет учитывать искажение формы входного воздействия, но при этом не учитывается задержка сигнала во времени. На рис. 4.20 показана схема замещения воздушной линии, которая используется в инженерных расчетах при всех напряжениях свыше 35 кВ [38, 41].
Параметры схемы замещения линии длиной менее 300 км определяются следующим образом: R = R0l, X = X0l, B = B0l. Для подавляющего большинства воздушных линий потери на корону при инженерных расчетах вообще не учитываются.
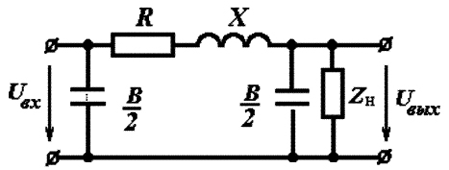
Рис. 4.20. П-образная схема замещения линии электропередачи
Рассмотрим методику численного моделирования динамических характеристик линии по выражению передаточной функции (4.30) [93]. При моделировании были приняты следующие допущения:
1) первичные параметры линии R0, L0, С0, G0 являются величинами постоянными и не зависящими от частоты;
2) в качестве схемы замещения элементарного участка линии используется схема с последовательным соединением R0, L0 элементов в продольной цепи и параллельным соединением С0, G0 элементов в поперечной ветви (рис. 4.18);
3) пренебрегаем влиянием внешних факторов на параметры цепи, например погодных условий.
Выражение передаточной функции по напряжению однородной цепной схемы имеет вид:
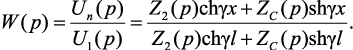(4.31)
Выразим гиперболические функции в выражении (4.31) через экспоненциальные, используя соотношения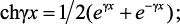 
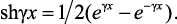В результате получим:
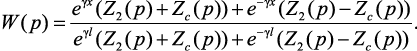(4.32)
Рассмотрим задачу z-моделирования переходных процессов в однородной двухпроводной линии с распределенными параметрами, имеющую активно-индуктивный нагрузку с сосредоточенными параметрами и источник питания на одном конце. Необходимо отметить, что была использована форма передаточной функции с координатой x относительно конца линии. Это связано с тем, что для моделирования электропередачи эта форма наиболее удобна, то есть она позволяет производить анализ реакций в конце линии. Проведем сравнительный анализ
переходных функций длинной линии, полученных эталонным методом и методом z-форм, и анализ погрешностей.
Поскольку в выражении (4.32) Zc(p) и γ(p) представлены в виде радикалов, то для дискретизации передаточной функции необходимо выбрать способы аппроксимации выражений Zc(p) и γ(p), позволяющих получить достаточно точную модель. Для аппроксимации Zc(p) и γ(p) выполним разложение в ряд Маклорена выражений (4.23) и (4.24) и ограничимся двумя первыми членами ряда:
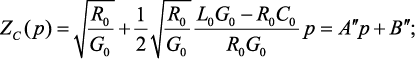(4.33)
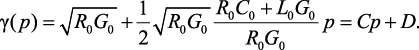(4.34)
При дискретизации ZС(p) и Z2(p) необходимо выбрать одну из z-форм. В проведенном исследовании использовался переход к z-изображению с помощью метода обратной разности, поскольку данный метод согласно проведенным исследованиям конформных отображений имеет запас по устойчивости по сравнению с другими z-формами. Это важно для исследуемой модели линии, в которой регулируются степени полиномов числителя и знаменателя в зависимости от длины участка, на котором проводится моделирование, и, соответственно, изменяется число полюсов и нулей передаточной функции, что влияет на устойчивость численного решения.
При переходе от аналоговой передаточной функции к дискретной выполним замену аргумента p на z в выражениях ZС(p) и eγx. Так, например, для перехода в выражении eγx используем упрощенное выраже-
ние (4.34) и форму замены аргумента при дискретизации z = epTx:
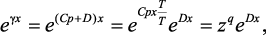(4.35)
где q = Cx/T, T – временной период дискретизации. Заметим, что гиперболические функции просто реализуются в области z-переменной, причем без упрощений.
Так, например, получено выражение для ZC(z):
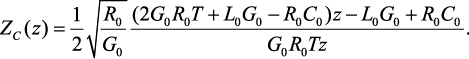(4.36)
Выполнив преобразование по формуле (4.35) и подстановку в формулу (4.32), получим дискретную передаточную функцию линии:
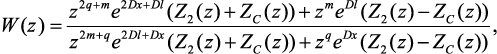(4.37)
где m = Cl/T.
В результате использования аппарата z-преобразования получено выражение дискретной передаточной функции, оригинал которой определяется сравнительно просто с помощью рекуррентной формулы. К тому же данная модель очень удобна для компьютерного анализа, а погрешностью моделирования можно управлять изменением временных и пространственных периодов дискретизации.
Из (4.37) получим выражение дискретной передаточной функции, позволяющей определять реакцию системы на внешнее воздействие в конце линии:
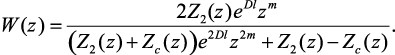(4.38)
При согласованной нагрузке Z2(z) = ZC(z), тогда из (4.38) получим:
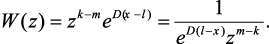(4.39)
При х = 0 выражение (4.39) примет вид:
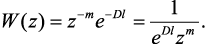(4.40)
Анализ выражения (4.40) показывает, что при прохождении сигнала в линии без искажений при согласованной нагрузке его амплитуда уменьшается в eDl раз, и осуществляется временная задержка сигнала на m отсчетов.
Для выбора временного периода дискретизации необходима информация о динамических свойствах объекта. В уравнении передаточной функции эта информация содержится в выражении волнового сопротивления линии. В результате разложения выражения (4.23) в ряд Тейлора получено упрощенное выражение (4.33), которое соответствует операторному сопротивлению активно-индуктивной цепи. По этому уравнению определим корень характеристического уравнения, величина обратная корню имеет размерность времени и может быть использована для определения периода дискретизации. Необходимо отметить, что аппроксимированная форма волнового сопротивления не оказывает существенного влияния на точность численного моделирования. Однако
экспериментальные исследования подтверждают, что первичные параметры линии оказывают влияние на устойчивость численной модели, например, при B′′ < 0 в выражении (4.33), получается неустойчивое численное решение. Это значит, что при использовании аппроксимированных выражений (4.33), (4.34) между первичными параметрами линии должно выполняться условие L0G0 > R0C0.
Для определения длины участка линии, на котором проводится моделирование, необходимо использовать выражение, полученное в результате дискретизации экспоненциальной функции (4.35), где q = Cl/T. Из этого выражения, задавшись порядком q, определяется длина исследуемого участка линии l.
Эталонный метод. Основной проблемой при анализе погрешностей моделирования в данной задаче является выбор точного решения в качестве эталонной функции. В качестве такой функции было использовано решение, полученное спектральным методом [29, 55, 56].
Зная спектральный состав входного воздействия Fвх(jω), который определяется согласно прямому преобразованию Фурье, и частотную характеристику цепи W(jω), можно определить спектральный состав выходной величины, оценить влияние частотной характеристики на выходное напряжение или ток.
Спектральная характеристика выходного напряжения четырехполюсника имеет вид:
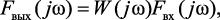(4.41)
где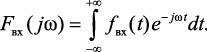 
Согласно обратному преобразованию Фурье по спектральной характеристике выходного сигнала определим оригинал
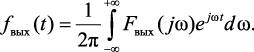(4.42)
Заметим, что ступенчатые и гармонические воздействия не являются абсолютно интегрируемыми в бесконечных пределах. Спектральные характеристики таких функций не могут быть получены из соответствующих изображений по Лапласу путем замены p на jω, иначе можно потерять импульсную компоненту в виде дельта функции. Спектральная характеристика единичной функции [6]:
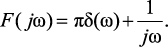(4.43)
Зная комплексную спектральную плотность искомой реакции, определим саму реакцию с помощью обратного преобразования Фурье:
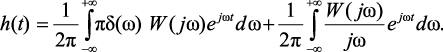(4.44)
Частотная характеристика линии получена путем замены оператора p в выражении (4.31) на jω. Представим выражение W(jω) в показательной форме записи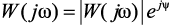 
, где |W(jω)| – амплитудно-частотная характеристика, 
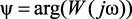– фазо-частотная характеристика, тогда
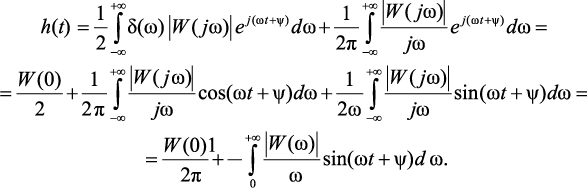(4.45)
Поскольку входное воздействие содержит бесконечное число гармонических составляющих, при решении спектральным методом их число необходимо ограничить.
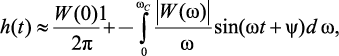(4.46)
где ωc – частота среза. Для определения частоты среза воспользуемся амплитудно-частотными характеристиками линии |W(ω)|. Выберем ωс таким образом, чтобы значение |W(ωc)| составляло не более 1 % от |W(ω)|max.
Рассмотрим методику цифрового моделирования переходных процессов в длинной линии с помощью z-форм, в качестве модели рассмотрим передаточную функцию линии. При моделировании необходимо соблюдать следующее ограничение: выполнение условия L0G0 > R0C0. между первичными параметрами линии.
Методика моделирования
Выберем форму аппроксимации. Для моделирования воспользуемся методом обратной разности, так как согласно анализу конформных преобразований областей устойчивости этот метод обеспечивает наибольший запас по устойчивости.
Перейдем от аналоговой передаточной функции (4.31) к дискретной. Определим Zc(p) и γ(p) по аппроксимированным выражениям (4.33) и (4.34) и осуществим замену аргумента p на z с помощью подстановки p = (z – 1)/(zT) согласно обратной разности. Дискретизация экспоненциальных функций осуществляется по формуле (4.35):
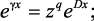
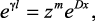
где q, m задаются предварительно.
Выберем значение периода дискретизации. Определим постоянную времени линии по формуле
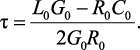
Выберем период дискретизации на два порядка меньше постоянной времени линии.
Определим длину участка линии, на котором проводится моделирование. Длина участка моделирования определяется по выражению l = mT/C, где m – показатель степени звена запаздывания, полученного при дискретизации экспоненциальной функции (задается предварительно).
Определим значения функции оригинала с помощью разностного выражения (1.105).
Пример 4.1. В настоящее время отсутствуют методики моделирования динамических характеристик линии по выражению передаточной функции, поэтому, чтобы оценить точность моделирования линии проведем исследования для частного случая, для которого из литературных источников известна форма реакции, а именно для линии без искажений при согласованной нагрузке. Сигнал, проходящий по линии без искажений, не изменяет своей формы и запаздывает по времени [7]. В линии без искажений волновое сопротивление является вещественным числом. Для согласования нагрузки необходимо, чтобы Lн было равно нулю, тогда R2 = ZC. В нашем случае использовались параметры: Rн = ZC = 27713 Ом; L2 = 0; R0 = 38,4∙10–3 Ом/м; L0 = 3,93∙10–3 Гн/м; C0 = 5,12∙10–12 Ф/м; G0 = 5∙10–11 См/м; m = 20; q = 0; l = 140955 м; Т = 0,001 с, число итераций N = 1000; 0 < ω < 1000 рад/с. Расчеты выполнены с помощью пакета математических программ Maple 11.
Выражения (4.33), (4.34), (4.40) с численными значениями имеют вид:
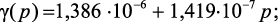(4.47)
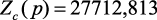Ом; (4.48)
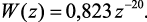(4.49)
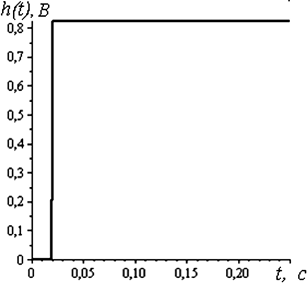
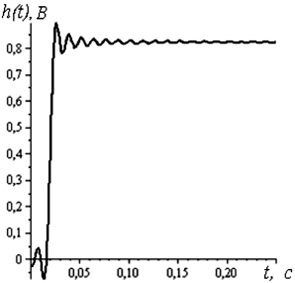
На рис. 4.21 представлены графики переходных функций, полученных с помощью спектрального метода и метода z-форм для линии без искажений и согласованной нагрузке. График относительной погрешности представлен на рис. 4.22.
а б
Рис. 4.21. Переходные характеристики линии без искажений
с согласованной нагрузкой, полученные с помощью:
а – метода z-форм, б – спектрального метода
Из анализа графиков функций (рис. 4.21) следует, что при передаче сигналов в линии без искажений с согласованной нагрузкой моделирование спектральным методом дает погрешность по сравнению с предложенным методом.
Таким образом, на простом примере показана эффективность и высокая точность численного метода моделирования длинной линии на основе ее дискретной передаточной функции. Погрешность образцового метода (рис. 4.22) возникает из-за ограничения диапазона частот. Необходимо отметить, что расчет с помощью z-преобразования превосходит по быстродействию расчет спектральным методом и может быть использован в реальном времени.
Пример 4.2. На основе выражения (4.38) получена дискретная передаточная функция линии без искажений c не согласованной нагрузкой:
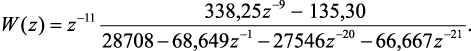(4.50)
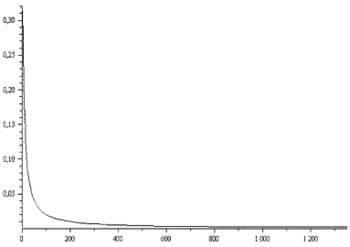
На рис. 4.23, а представлены две переходные функции, полученные спектральным методом и методом z-форм для линии без искажений с не согласованной нагрузкой, которые практически совпадают.
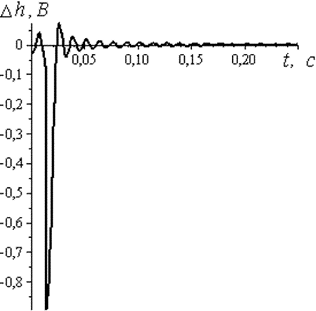
Рис. 4.22. График абсолютной погрешности спектрального метода для линии без искажений с согласованной нагрузкой
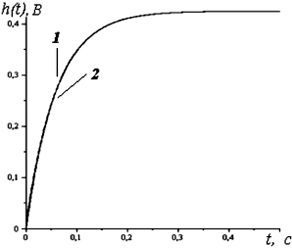
а б
Рис. 4.23. Графики:
а – переходных характеристик, полученных спектральным методом (1)
и методом z-форм (2) для линии без искажений с не согласованной нагрузкой; б – относительной погрешности спектрального метода
Расчеты выполнены с помощью пакета математических программ Maple 11 при Rн = 100 Ом; L2 = 0,01 Гн; L2 = 0; R0 = 38,4∙10–3 Ом/м; L0 = 3,93∙10–3 Гн/м; C0 = 5,12∙10–12 Ф/м; G0 = 5∙10–11 См/м; m = 10; q = 0; l = 10574 м; Т = 0,0001 с; число итераций N = 6666; 0 < ω < 1000 рад/с. На рис. 4.23, б представлен график относительной погрешности спектрального метода.
Пример 4.3. Рассмотрим наиболее общий случай, а именно проведем исследование динамических характеристик линии с искажениями при следующих параметрах: Rн = 100 Ом; L2 = 0,01 Гн; R0 = 38,4∙10–3 Ом/м; L0 = 8,84∙10–3 Гн/м; C0 = 5,12∙10–12 Ф/м; G0 = 5∙10–11 См/м; m = 20; q = 0; l = 86791 м; Т = 0,001 с; число итераций N = 1000; 0 < ω < 1000 рад/с. При решении данной задачи использовались параметры нагрузки параметры стальной воздушной двухпроводной линии, определенные при сухой погоде, расстояние между осями проводов 60 см, их диаметр 4 мм [50, 61].
Для ограничения гармонических составляющих при вычислении эталонной функции воспользуемся амплитудно-частотной характеристикой линии (рис. 4.24). При ω = 1000 рад/с – |W(ω)| = 0,0035 В, что составляет ≈ 1 % от |W(ω)|max. При расчете переходной функции эталонным методом выбрана частота среза – ωс = 1000 рад/с.
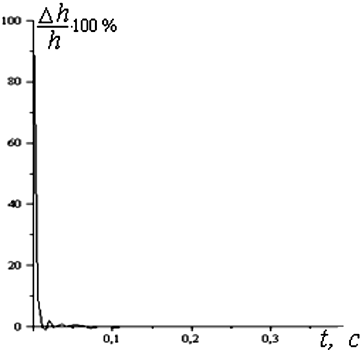
Рис. 4.24. График амплитудно-частотной характеристики линии
Выражения (4.33), (4.34),(4.40) с численными значениями имеют вид:
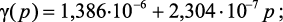(4.51)
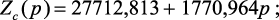(4.52)
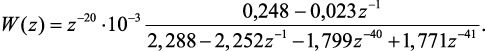(4.53)
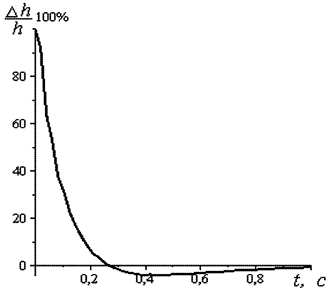
Переходные характеристики, полученные с помощью спектрального метода и метода z-форм для линии c искажениями и не согласованной нагрузкой представлены на рис. 4.25, а. Максимальная абсолютная погрешность моделирования – 0,0037 В. График относительной погрешности показан на рис. 4.25, б.
а б
Рис. 4.25. Графики:
а – переходных характеристик, полученных спектральным методом (1) и методом z-форм (2) для линии c искажениями, абсолютной погрешности; б – относительной погрешности
Инженерный расчет. На рис. 4.20 показана схема замещения воздушной линии, которая используется в инженерных расчетах при всех напряжениях свыше 35 кВ. Проведем исследование переходного процесса в линии при единичном ступенчатом воздействии, рассматривая линию как четырехполюсник с сосредоточенными параметрами. Операторная схема замещения четырехполюсника с активно-индуктивной нагрузкой Zн(p) = pLн + Rн изображена на рис. 4.26. Сравним результаты данного расчета с результатами, полученными ранее спектральным методом для линии с искажениями. Составим операторную схему замещения линии.
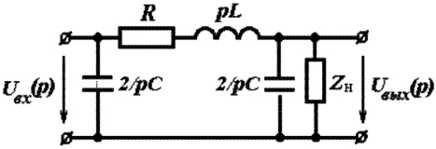
Рис. 4.26. Операторная схема замещения длинной линии
Передаточная функция линии имеет следующий вид:
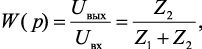(4.54)
где
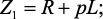
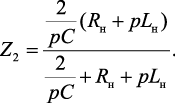(4.55)
Получим передаточную функцию с численными коэффициентами:
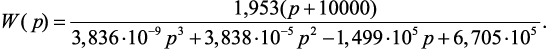(4.56)
Согласно обратному преобразованию Лапласа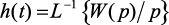 
получено выражение переходной характеристики:
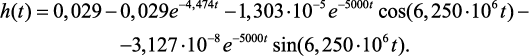(4.57)
На рис. 4.27 представлены графические зависимости, полученные с использованием упрощенных схем замещения линии и спектральным методом (программа Maple 11), которые практически совпадают. Максимальная абсолютная погрешности – 0,0015. Это связано с тем, что в обоих случаях используются различные упрощения, в первом случае для расчетов применяются упрощенные схемы замещения линии. Во втором случае при вычислении значений переходной функции ограничивается число гармонических составляющих.
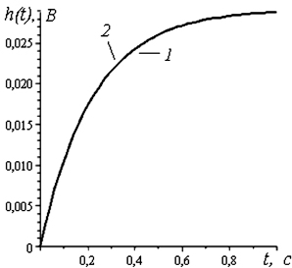
Рис. 4.27. Переходные характеристики, полученные с использованием упрощенных схем замещения линии (1) и спектральным методом (2)
Выводы. В результате использования аппарата z-преобразования получено выражение дискретной передаточной функции линии с распределенными параметрами удобное для цифровой обработки сигналов и синтеза цифровых регуляторов. Причем полученная дискретная модель учитывает процессы запаздывания и искажения сигналов присущие линии с распределенными параметрами. Необходимо отметить, что наиболее просто, без потерь осуществляется моделирование процесса запаздывания. Аппроксимация использована при моделировании процессов искажения сигналов. Приведенная модель передаточной функции позволяет моделировать системы с регулированием напряжения не на входе линии, а на ее выходе. Необходимо отметить, что при расчете спектральным методом h(t) ≠ 0 при t = 0, то есть реакция появляется одновременно с возмущающим воздействием, поскольку линия вносит искажение сигнала и запаздывание, это противоречит физике процесса. В предлагаемой методике такого эффекта не наблюдается.
В связи с отсутствием методик моделирования линии с распределенными параметрами по выражению передаточной функции, адекватность модели проверялась на частном случае, для которого известна форма реакции, а также на анализе реакций, полученных различными методами. На основании проведенных экспериментов выявлено, что наибольшее влияние на точность моделирования переходных процессов в линии оказывает аппроксимация выражений ZC(p) и γ(p) и их дискретизации.
Кроме того исследования показали, что при работе линии во всем частотном диапазоне при некоторых ее параметрах могут возникать неустойчивые решения. Это связано с тем, что используемые схемы замещения элементарного участка линии были разработаны для гармонических возмущающих воздействий, то есть могут работать в ограниченном частотном диапазоне. Для представленных в литературных источниках схем замещения элементарного участка линии отсутствуют рекомендации по их использованию. Очевидно, что ни одна из схем в широком диапазоне не работает и каждая применима для конкретной задачи. Поэтому при моделировании переходных процессов в линии необходим обоснованный выбор исходной модели. Таким образом, полученная дискретная передаточная функция может использоваться при анализе устойчивости протяженных энергетических систем, охваченных обратной связью.